Affiner Unterraum

Eine Ebene im dreidimensionalen Raum (blau) ist ein affiner Unterraum, der durch Verschiebung einer Ursprungsebene um einen Vektor (rot) hervorgeht

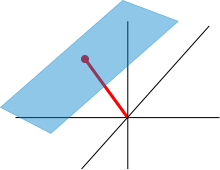
In der linearen Algebra ist ein affiner Unterraum eines Vektorraums eine Teilmenge, die durch Verschiebung aus einem Untervektorraum hervorgeht. Ein solcher affiner Unterraum ist auch ein affiner Raum im Sinne der analytischen Geometrie.

Definition

Eine Teilmenge $A$ eines Vektorraums $V$ heißt affiner Unterraum, wenn es einen Vektor $v$ aus $V$ und einen Untervektorraum $U_{A}$ von $V$ gibt, sodass

$A=v+U_{A}=\left\{v+u\mid u\in U_{A}\right\}$

gilt. In diesem Fall heißt $v$ auch Stützvektor von $A$ und $U_{A}$ der $A$ zugeordnete lineare Unterraum (der Verbindungsvektoren). $U_{A}$ ist durch $A$ eindeutig bestimmt; alle $w\in V$ mit $v-w\in U_{A}$ sind Stützvektoren von $A$. Die Dimension von $A$ ist die Dimension von $U_{A}$.

Ein eindimensionaler affiner Unterraum heißt affine Gerade. Ein zweidimensionaler affiner Unterraum heißt affine Ebene.

Hat der zu einem affinen Unterraum $A$ gehörige lineare Unterraum $U_{A}$ die Kodimension $1$, so nennt man $A$ eine affine Hyperebene.

In der analytischen Geometrie wird gelegentlich auch die leere Menge als affiner Unterraum bezeichnet. Sie hat dann als affiner Raum die Dimension $\dim \emptyset =-1$ und ihr ist kein linearer Unterraum zugeordnet.

Anschauliche Betrachtung

Als Untervektorraum $U$ werde eine Ursprungsgerade im dreidimensionalen Vektorraum $\mathbb {R} ^{3}$ gewählt, für die gilt:

$g\colon \ {\vec {x}}=\lambda \ {\begin{pmatrix}0\\0\\1\end{pmatrix}}$ mit $\lambda \in \mathbb {R}$

Als Vektor ${\vec {v}}\in V$ wird

${\vec {v}}={\begin{pmatrix}1\\0\\0\end{pmatrix}}$

gewählt. Dann ist der affine Unterraum $A={\vec {v}}+U$ eine Gerade, die um $(1|0|0)$ (also um eine Einheit in $x_{1}$-Richtung) verschoben ist, mit der Gleichung:

$h\colon \ {\vec {x}}={\begin{pmatrix}1\\0\\0\end{pmatrix}}+\mu \ {\begin{pmatrix}0\\0\\1\end{pmatrix}}$ mit $\mu \in \mathbb {R}$

Die auf diese Weise entstehende verschobene Gerade ist ein affiner Unterraum, aber kein Untervektorraum von $V$, da sie den Nullvektor nicht enthält.

Dimensionsformel für affine Unterräume

Sei $V$ ein endlichdimensionaler Vektorraum über einem Körper $K$ und seien $A,B$ zwei affine Unterräume von $V$.

Für den Fall, dass $A$ und $B$ nicht disjunkt sind oder einer der beiden Räume leer ist, gilt die Dimensionsformel:

$\dim(A)+\dim(B)=\dim(A\vee B)+\dim(A\cap B)$

Falls $A$ und $B$ jedoch disjunkt und nichtleer sind, lautet die Dimensionsformel

$\dim(A)+\dim(B)=\dim(A\vee B)+\dim(U_{A}\cap U_{B})-1,$

wobei $U_{A}$ aus der Darstellung $A=v+U_{A}$ (mit festem $v\in A$ und dem zugeordneten linearen Unterraum $U_{A}$ von $V$) erhalten wird. Analog erhält man $U_{B}$.

In beiden Fällen steht $A\vee B$ für den Verbindungsraum von $A$ und $B$.

Eigenschaften

Da in der Definition eines affinen Unterraums auch $v=0$ gewählt werden kann, ist jeder Untervektorraum gleichzeitig affiner Unterraum. Ein affiner Unterraum ist genau dann ein Untervektorraum, wenn er den Nullvektor enthält.

Der Lösungsraum eines inhomogenen linearen Gleichungssystems in $n$ Variablen über dem Körper $K$ ist ein affiner Unterraum von $K^{n}$, falls die Lösungsmenge nicht leer ist. Jeder affine Unterraum kann durch ein solches Gleichungssystem beschrieben werden. Alternativ kann ein affiner Unterraum auch als affine Hülle von Vektoren oder, wie direkt aus der Definition folgt, mit Hilfe eines Stützvektors und einer Basis des Untervektorraums angegeben werden.

Literatur

• Gerd Fischer: Lineare Algebra. ISBN 3-528-03217-0, S. 166 ff. (Auszug (Google)}).
• Siegfried Bosch: Lineare Algebra. ISBN 978-3-540-76437-3, S. 65 ff.