Computer Vision

Computer Vision ist eine Wissenschaft im Grenzbereich zwischen Informatik und den Ingenieurwissenschaften und versucht die von Kameras aufgenommenen Bilder auf unterschiedlichste Art und Weise zu verarbeiten und zu analysieren, um deren Inhalt zu verstehen oder geometrische Informationen zu extrahieren. Der Begriff Computer Vision bedeutet auf Deutsch so viel wie computerbasiertes Sehen (oder kurz: Computer-Sehen). Im englischen Sprachraum wird ebenfalls der Begriff Machine Vision (auf Deutsch: Maschinelles Sehen) synonym zu Computer Vision verwendet, wobei die Anwendung im industriellen Umfeld betont wird.

Typische Aufgaben der Computer Vision sind die Objekterkennung und die Vermessung der geometrischen Struktur von Objekten sowie von Bewegungen (Fremdbewegung, Eigenbewegung). Dabei wird auf Algorithmen aus der Bildverarbeitung zurückgegriffen, zum Beispiel die Segmentierung und auf Verfahren der Mustererkennung, beispielsweise zur Klassifizierung von Objekten. Dabei kommen statistische (bzw. probabilistische) Methoden zum Einsatz, Methoden der Bildverarbeitung, der projektiven Geometrie, aus der Künstlichen Intelligenz und der Computergrafik. Die Werkzeuge stammen meistens aus der Mathematik, insbesondere aus Geometrie, linearer Algebra, Statistik, Operations Research (Optimierung) und Funktionalanalysis. Darüber hinaus besteht eine enge Verwandtschaft zu benachbarten Fachgebieten, wie der Photogrammetrie, der Fernerkundung und der Kartografie.^[1]^[2]^[3]

Anwendungsgebiete sind z. B. die autonome Navigation von Robotern (Fahrerassistenzsysteme), die Filmindustrie zur Erschaffung virtueller Welten (virtual reality), die Spieleindustrie zum Eintauchen und Interagieren in virtuellen Räumen (augmented reality), die Erkennung und Verfolgung von Objekten (z. B. Fußgänger) oder die Registrierung von medizinischen CT-Aufnahmen und die Erkennung von krankem Gewebe.

Geschichte

Seit ungefähr den 1960er Jahren gab es erste Versuche eine Szene durch Kantenextraktion und ihrer topologischen Struktur zu verstehen. Die Extraktion verschiedener Merkmale, wie Kanten und Ecken, war in den 1970er bis 1980er Jahren ein aktives Forschungsgebiet. Anfang der 1980er Jahre wurde untersucht, wie Variationen von Schattierungen durch topografische (Höhen-)Änderungen verursacht werden und damit der Grundstein für Fotometrie und die 3D-Rekonstruktion mittels Schattenwurf gelegt. Gleichzeitig wurden erste merkmalsbasierte Stereo-Korrespondenz-Algorithmen entwickelt sowie intensitätsbasierte Algorithmen zur Berechnung des optischen Fluss. Außerdem wurden 1979 erste Arbeiten zur simultanen Wiederherstellung der 3D-Struktur und der Kamerabewegung (Structure from Motion) begonnen.

Mit dem Aufkommen digitaler Kameras in den 1980er Jahren wurden mehr und mehr Anwendungen erforscht und entwickelt. So wurden Bildpyramiden erstmals 1980 von Rosenfeld eingesetzt als Grob-zu-Fein-Strategie zur Suche homologer Bildpunkte (Korrespondenz-Suche). Auch das Konzept des Maßstabsraumes (scale-space) beruht auf Bildpyramiden und wurde maßgeblich erforscht, was die Grundlage moderner Methoden wie SIFT (Scale Invariant Feature Transform) ist.

Ab den 1990er Jahren begann man projektive Invarianten zu untersuchen, um Probleme zu lösen wie Struktur-aus-Bewegung (structure from motion) und projektive 3D-Rekonstruktion, die ohne Kenntnis der Kamerakalibrierung auskommt. Gleichzeitig wurden effiziente Algorithmen entwickelt wie Faktorisierungstechniken und globale Optimierungsalgorithmen.^[4]

Seitdem es günstige Kameras gibt und die PCs immer leistungsfähiger wurden, bekam dieses Fachgebiet einen enormen Aufschwung.

Komplexität

Die Aufgabenstellungen sind oftmals inverse Probleme, wo versucht wird, aus zweidimensionalen Abbildungen die Komplexität der dreidimensionalen Welt wieder herzustellen. Computer Vision versucht aus Bildern Eigenschaften zu rekonstruieren, wie die farbliche Gestalt, die Beleuchtung oder deren Form, und darauf basierend versucht man z. B. Gesichter zu erkennen, landwirtschaftliche Flächen zu klassifizieren oder komplexe Objekte zu erkennen (PKW, Fahrrad, Fußgänger). All das gelingt einem Menschen scheinbar spielerisch, es ist aber extrem schwer dies einem Computer beizubringen.

Der Versuch, unsere sichtbare Welt in all seiner Gesamtheit modellieren zu wollen, ist bei weitem schwerer, als beispielsweise eine Computer-generierte künstliche Stimme zu erzeugen (Szeliski 2010, S. 3).^[4] Dies wird von Wissenschaftlern, die nicht in diesem Gebiet arbeiten, oft unterschätzt, wie schwierig die Probleme sind und wie fehleranfällig darum deren Lösungen teilweise sind. Das führt einerseits dazu, dass man für Problemstellungen oft maßgeschneiderte Lösungen braucht. Andererseits wird dadurch jedoch deren Vielseitigkeit stark beschränkt. Unter anderem aus diesem Grunde gibt es für keine Aufgabenstellung nur eine Lösung, sondern viele verschiedene Lösungen, je nach den Anforderungen, und erklärt damit auch, warum so viele konkurrierende Lösungswege in der Fachwelt existieren.

Überblick der Methodik

Die eigentliche Aufgabe des Computer Vision besteht darin, einer am Computer angeschlossenen Kamera das Sehen und Verstehen beizubringen. Dafür sind verschiedene Schritte notwendig und es gibt je nach Aufgabenstellung entsprechende unterschiedliche Methoden. Diese sollen hier kurz skizziert werden.

Zunächst einmal benötigt man ein aufgenommenes Bild (Abschnitt Bildentstehung) welches meist verbessert werden muss (z. B. Helligkeits- und Kontrastausgleich). Anschließend versucht man meist Merkmale zu extrahieren wie Kanten oder Eckpunkte (Abschnitt Merkmalsextraktion). Je nach Aufgabenstellung verwendet man z. B. Eckpunkte für die Korrespondenzsuche in Stereo-Bildern. Darüber hinaus können weitere geometrische Elemente wie Geraden und Kreise mittels der Hough-Transformation erkannt werden (Abschnitt Hough-Transformation). Bestimmte Anwendungen versuchen mittels Bildsegmentierung uninteressante Bildbestandteile wie den Himmel oder den unbewegten Hintergrund zu selektieren (Abschnitt Bildsegmentierung).

Möchte man eine Kamera zum Messen einsetzen werden i. d. R. die Parameter des Kameramodells (innere Orientierung) durch eine Kamerakalibrierung bestimmt (Abschnitt Kamerakalibrierung). Um die gegenseitige Lage eines Stereo-Bildpaars aus dem Bildinhalt zu schätzen, kommen verschiedene Algorithmen zur Berechnung der Fundamentalmatrix zum Einsatz (siehe Epipolargeometrie Fundamentalmatrix).

Bevor man eine 3D-Rekonstruktion durchführen kann, benötigt man zunächst homologe (korrespondierende) Bildpunkte (Abschnitt Korrespondenzproblem). Anschließend ist man in der Lage die 3D-Punkte durch Vorwärtsschnitt (Triangulation) zu bestimmen. Daneben gibt es verschiedene Möglichkeiten die Form eines Objektes dreidimensional zu bestimmen. Im englischen Sprachgebrauch hat sich hier der Terminus Shape-from-X eingebürgert. Das X steht hierbei für eine dieser Methoden (Abschnitt Shape-from-X).

Bildentstehung

Die Bildentstehung beschreibt den komplexen Prozess der Bildaufnahme beginnend bei der elektromagnetischen Strahlung, der Interaktion mit der Oberfläche (Absorption und Reflexion), der optischen Abbildung und der Detektion mittels Kamerasensoren.

Lochkameramodell

Neben anderen Möglichkeiten eine Kamera zu modellieren ist das am häufigsten verwendete Modell die Lochkamera. Die Lochkamera ist ein idealisiertes Modell einer Kamera, welches eine Realisierung des geometrischen Modells der Zentralprojektion darstellt. Mittels Strahlensätze lassen sich damit auf einfache Art und Weise Abbildungsformeln herleiten.

Reale Kamera

Aufbau einer modernen digitalen Farbkamera

Eine reale Kamera weicht in vielerlei Hinsicht vom Lochkameramodell ab. Man benötigt Linsen, um mehr Licht einzufangen und einen lichtempfindlichen Sensor um das Bild zu erfassen und zu speichern. Dabei kommt es zu diversen Abweichungen, die einerseits physikalisch bedingt sind und andererseits durch unvermeidliche Fertigungsungenauigkeiten entstehen. Beides führt zu Verzerrungen im aufgenommenen Bild. Sie werden einerseits durch den Sensor und andererseits durch das Objektiv verursacht.

Es kommt beim Sensor zu farblichen Abweichungen (radiometrische bzw. fotometrische Abweichung) und geometrischen Abweichungen (Verzeichnung). Abweichungen, die durch das Objektiv, also durch die einzelnen Linsen verursacht werden, bezeichnet man als Aberrationen. Sie führt ebenfalls zu farblichen Abweichungen (z. B. Farbsäume) und geometrischen Verzerrungen (Verzeichnung).

Es kommt außerdem zu atmosphärischer Refraktion (Lichtbrechung). Im Nahbereich ist der Effekt jedoch so gering, dass man ihn meist vernachlässigen kann.

Digitale Sensoren

Zur Detektion des Lichts benötigt man lichtempfindliche Sensoren, die Licht in Strom umwandeln können. Schon 1970 wurde ein CCD-Sensor (Englisch: charge coupled device, auf Deutsch: ladungsgekoppeltes Bauelement) zur Bildaufnahme entwickelt. Durch Aneinanderreihung in einer Zeile erhält man einen Zeilensensor und entsprechende Anordnung in einer Fläche erhält man einen flächenhaften Sensor. Jedes einzelne Element wird dabei als Pixel (Englisch: picture element) bezeichnet.

Alternativ dazu gibt es auch einen flächenhaften Sensor CMOS (Englisch: complementary metal-oxide-semiconductor, auf Deutsch: komplementärer / sich ergänzender Metall-Oxid-Halbleiter) genannt.

Prinzip einer 3-Sensor-Farbkamera mittels Strahlteiler

Ein solcher Sensor ist in der Regel über das Spektrum des sichtbaren Lichtes hinaus empfindlich im ultra-violetten Bereich und weit in den infraroten Bereich des Lichts. Um ein Farbbild aufnehmen zu können, muss man für die jeweiligen Grundfarben Rot, Grün und Blau (kurz: RGB) einen eigenen Sensor haben. Dies kann man durch Aufteilung des Lichtes auf drei unterschiedliche Flächen machen (s. Abb. rechts). Eine andere Möglichkeit besteht darin, nebeneinander liegende Pixel jeweils mit unterschiedlichen Farbfiltern zu versehen. Meist wird dafür ein von Bayer entwickeltes Muster verwendet (Bayer pattern).

Darüber hinaus sind auch andere – meist wissenschaftlich motivierte – Farbkanäle im Einsatz.

Kamerakalibrierung

Im engeren Sinne wird unter einer Kamerakalibrierung die Bestimmung der inneren Orientierung verstanden. Dies sind alle Modellparameter, welche die Kamerageometrie beschreiben. Dazu zählen i. d. R. die Koordinaten des Hauptpunktes, die Kamerakonstante sowie Verzeichnungsparameter. Im weiteren Sinne wird unter einer Kamerakalibrierung aber auch die gleichzeitige Bestimmung der äußeren Orientierung verstanden. Da man sowieso meistens beides bestimmen muss, zumindest wenn man eine Kalibrierung mittels bekannten 3D-Koordinaten durchführt, wird dies im Computer Vision oft synonym verwendet. In der Photogrammetrie hingegen ist es durchaus noch üblich eine Laborkalibierung (z. B. mittels Goniometer) auszuführen, wo die innere Orientierung direkt bestimmt werden kann.

Am häufigsten wird eine Kamera mittels eines bekannten Testfeldes oder Kalibrierrahmen kalibriert. Dabei sind die 3D-Koordinaten gegeben und die abgebildeten Bildkoordinaten werden gemessen. Somit kann man mittels den bekannten Abbildungsbeziehungen ein Gleichungssystem aufstellen, um die Parameter des Abbildungsmodells zu bestimmen. Abhängig von den Genauigkeitsanforderungen verwendet man ein geeignetes Kameramodell. Eine genaues Modell ist in der Abbildung dargestellt (s. Abb. rechts).

Optische Begriffe in Kameras

Gegenüber dem Lochkameramodell weicht eine reale Kamera in vielerlei Hinsicht ab. Es ist deswegen notwendig einige optische Begriffe zu definieren.^[5]

Ein Objektiv enthält meistens eine Blende (oder die Fassung der Linsen, die genauso wirkt) und es stellt sich die Frage: Wo ist das Projektionszentrum? Je nachdem, von welcher Seite man ins Objektiv guckt, sieht man ein anderes Bild der Blende. Die beiden Bilder lassen sich nach den Regeln der geometrischen Optik konstruieren. Das Licht tritt aus dem Objektraum (in Abb. von links) ins Objektiv ein und erzeugt als Bild der Blende die Eintrittspupille (EP). Zum Bildraum hin tritt das Licht wieder aus und erzeugt die Austrittspupille (AP). Die jeweiligen Mittelpunkte der Eintrittspupille und der Austrittspupille liegen auf der optischen Achse und sind die Punkte, durch die der Hauptstrahl (entspricht dem Projektionsstrahl im Lochkameramodell) ungebrochen hindurchgeht. Deswegen ist der Mittelpunkt der EP das Projektionszentrum $O$ und der Mittelpunkt der AP das bildseitige Projektionszentrum $O\ '$ .

Um den Bezug herzustellen zwischen einem Kamerakoordinatensystem und einem Bildkoordinatensystem, benutzt man das bildseitige Projektionszentrum $O\ '$ . Es wird senkrecht in die Bildebene projiziert und erzeugt den Hauptpunkt $H$ . Der Abstand zwischen $O\ '$ und $H$ ist definiert als die Kamerakonstante $c$ . Aufgrund von unvermeidbaren Fertigungsungenauigkeiten, steht die Verlängerung der optischen Achse nicht (exakt) senkrecht auf der Bildebene und erzeugt als Durchstoßpunkt den Symmetriepunkt der Verzeichnung $S$ (auch Verzeichnungszentrum genannt). Es ist jedoch oft üblich für die rechnerische Bestimmung das Verzeichnungszentrum mit dem Hauptpunkt gleichzusetzen. Denn die beiden Punkte liegen meist eng beieinander, wodurch es zu einer starken Korrelation kommt. Darunter leidet die Präzision während der Kamerakalibrierung.

Um die Aufnahmerichtung zu definieren, stelle man sich vor, man würde den Hauptpunkt in den Objektraum zurückprojizieren. Weil dieser Strahl durch das bildseitige Projektionszentrum $O\ '$ geht, muss er ebenfalls durchs Projektionszentrum $O$ gehen. Dieser eine Strahl ist also quasi ein Hauptstrahl und darüber hinaus der einzige Strahl, der senkrecht auf die Bildebene projiziert wird. Damit entspricht dieser Strahl der Aufnahmeachse und ist gleichzeitig die Z-Achse des Kamerakoordinatensystems.

Der Winkel $\tau$ zwischen Aufnahmeachse und einem Objektpunkt $P$ ändert sich beim Austritt in den Bildraum und erzeugt den Bildpunkt $P'$ . Diese Winkeländerung ist Ausdruck von Verzeichnung.

Verzeichnungskorrektur

Bei Objektiven mit Verzeichnung wird ein Rechteck nicht maßstabsgetreu abgebildet

Verzeichnung umfasst alle durch das Objektiv verursachten Abweichungen gegenüber dem idealen Modell der Lochkamera. Daher muss der Fehler so korrigiert werden, als wenn die Bilder von einer perfekten linearen Kamera (Lochkamera) aufgenommen worden wären. Da die Linsenverzeichnung bei der ursprünglichen Abbildung des Objektpunktes auf das Bild auftritt, wird der dabei entstandene Fehler modelliert mit folgender Gleichung:

{\begin{pmatrix}y_{d}\\x_{d}\end{pmatrix}}=L({\tilde {r}}){\begin{pmatrix}{\tilde {y}}\\{\tilde {x}}\end{pmatrix}}

Dabei sind

$({\tilde {x}},{\tilde {y}})$ die idealen Bildpunkte ohne Verzeichnung,
$x_{d},y_{d}$ die verzeichneten Bildkoordinaten,
${\tilde {r}}$ der radialen Abstand ${\sqrt {{\tilde {x}}^{2}+{\tilde {y}}^{2}}}$ vom Verzeichnungszentrum (meist Bildmitte) und
$L({\tilde {r}})$ der Verzeichnisfaktor, welcher nur von ${\tilde {r}}$ abhängig ist.

Die Korrektur geschieht dann mittels

{\hat {x}}=x_{c}+L(r)(x-x_{c})\quad {\hat {y}}=y_{c}+L(r)(y-y_{c})

$x$ und $y$ sind die gemessenen, ${\hat {x}}$ und ${\hat {y}}$ die korrigierten Bildkoordinaten und $x_{c}$ , $y_{c}$ das Zentrum der Verzeichnung mit $r^{2}=(x-x_{c})^{2}+(y-y_{c})^{2}$ . $L$ ist nur definiert bei positiven $r$ . Eine Annäherung geschieht meist mittels Taylor-Approximation. Wegen der Symmetrie der Verzeichnungskurve bezüglich des Zentrums der Verzeichnung sind nur ungerade Potenzen notwendig (daher auch Seidel-Reihe genannt).^[6] $L$ ist dann

L(r)=k_{1}r+k_{2}r^{3}+k_{3}r^{5}+\ldots

Darüber hinaus besteht eine enge Korrelation zwischen dem ersten Term $k_{1}r$ und der Kamerakonstanten $c$ , wegen $\tan \tau ={\frac {r}{c}}$ . Deswegen wird der erste Term oft entfernt, wodurch die Präzision bei der Ausgleichung deutlich gesteigert werden kann.^[7]

Die Koeffizienten $k_{i}$ sind Teil der inneren Kalibrierung der Kamera. Sie werden meist mittels iterativer Verfahren der Ausgleichungsrechnung bestimmt.

Eine Möglichkeit ist die Verwendung von Geraden wie z. B. aufgehängte Lote. Diese müssen sich bei richtiger Korrektur in Geraden abbilden. Die Minimierung einer Kostenfunktion (zum Beispiel der Abstand der Linienenden zum Mittelpunkt) liefert dann die Lösung. Diese Methode ist auch als Plumbline-Kalibrierung bekannt.^[8]

Der Hauptpunkt wird meist – im Rahmen der Genauigkeitsanforderungen – als Zentrum der Verzeichnung angenommen. Die Verzeichniskorrektur zusammen mit der Kamerakalibrierungsmatrix beschreibt damit vollständig die Abbildung des Objektpunktes auf einen Bildpunkt.

Bildverarbeitung (Filterung, Glättung, Rauschunterdrückung)

Ziel: Beleuchtungskorrektur (exposure correction), Farbausgleich (color balancing), Unterdrückung von Bildrauschen, Verbesserung der Schärfe

Prinzip: lineare Filter, welche ein Signal falten (z. B. Differenzbildung zw. benachbarten Punkten)

Verschiedene Kernel und deren Wirkung (Differenz, Gauß)

Merkmalsextraktion und Mustererkennung (feature detection and pattern recognition)

Kantendetektion (edge detection)

Mit Hilfe unterschiedlicher Bildverarbeitungsalgorithmen versucht man Kanten zu extrahieren, um z. B. geometrische Modelle abzuleiten.

Eckendetektion (Punktdetektion, corner detection)

Ebenfalls mittels Methoden der Bildverarbeitung kann man Punkte extrahieren, die sich gut von der Umgebung abheben. Um solche Punkte zu finden, kommen Gradienten-Operatoren zum Einsatz, welche entlang zweier Hauptrichtungen benachbarte Pixel auf Änderung ihrer Helligkeitswerte untersuchen. Ein guter Punkt definiert sich dadurch, dass der Gradient entlang beider Hauptrichtungen möglichst groß ist. Dies lässt sich mathematisch als Fehlerellipse beschreiben, die möglichst klein sein sollte. Die Achsen der Fehlerellipse werden durch Berechnung der Eigenwerte der Kovarianzmatrix bestimmt (s. Förstner-Operator). Solche identifizierten Punkte haben vielfältige Anwendungszwecke u. a. zur Schätzung der Fundamentalmatrix (s. Fundamentalmatrix).

Bildsegmentierung (image segmentation)

Bei der Bildsegmentierung versucht man zusammenhängende Bildbereiche zu identifizieren. Dabei werden Methoden der Merkmalsextraktion kombiniert mit Bildbereichen, die ungefähr die gleiche Farbe haben. Prominentes Beispiel ist die Wasserscheidentransformation, womit man z. B. einzelne Ziegelsteine einer Hauswand extrahieren kann. Die Bildsegmentierung dient u. a. zur Klassifizierung verschiedener Flächen in der Fernerkundung und ermöglicht z. B. verschiedene Stadien des Pflanzenwachstums zu unterscheiden. In der Medizin kann dies die Detektion von krankem Gewebe in Röntgen- oder CT-aufnahmen unterstützen.

Hough-Transformation

Mittels der Hough-Transformation ist es möglich Linien und Kreise zu detektieren. Dies wird z. B. eingesetzt um Fahrbahnmarkierungen zu identifizieren (Spurhalteassistent) oder Straßenschilder.

Objekterkennung (object detection)

Objekterkennung ist ein komplexes Zusammenspiel von Merkmalsextraktion, Mustererkennung und selbst lernenden Entscheidungsalgorithmen der künstlichen Intelligenz. Z. B. möchte man für Fahrerassistenzsysteme Fußgänger von anderen Verkehrsteilnehmern unterscheiden wie PKW, Fahrrad, Motorrad, LKW usw.

Grundlagen der projektiven Geometrie

Konzept homogener Koordinaten

Homogene Koordinaten werden für die mathematische Beschreibung von projektiven Vorgängen vorteilhaft eingesetzt. Durch Hinzufügen einer weiteren Komponente zu einem zweidimensionalen Punktvektor, entsteht ein dreidimensionaler Vektor, wodurch Addition und Multiplikation in einer gesamten Transformationsmatrix ausgedrückt werden können. Hintereinandergereihte Transformationen können so zu einer einzigen gesamten Transformationsmatrix zusammengefasst werden. Neben dem Vorteil der kompakten Darstellung werden so Rundungsfehler vermieden.^[9]

Projektivtransformation (Homografie)

Häufig verwendet man eine projektive Transformation, um von einer Ebene in eine andere Ebene umzurechnen. Im englischen Sprachgebrauch wird dies als Homografie bezeichnet. Eine quadratische 3x3-Matrix $H$ mit vollem Rang beschreibt solch eine umkehrbar eindeutige Abbildung.

Standardabbildungsmodell (Zentralprojektion)

Hiermit wird die Abbildung eines Objektpunktes ins Bild beschrieben.

Korrespondenzproblem (Bildpunktzuordnung)

Die Suche nach einander zugeordneten (homologen) Bildpunkten zwischen Stereo-Bildern wird in Computer Vision als Korrespondenzproblem bezeichnet. Im englischen Fachjargon wird dies auch als image matching (Bildabgleich) bezeichnet. Dies ist ein Kernproblem, welches besonders schwierig ist, weil von der zweidimensionalen Abbildung auf ihre dreidimensionale Entsprechung rückgeschlossen wird. Es gibt deswegen viele Gründe, warum die Suche korrespondierender Bildpunkte fehlschlagen kann:^[7]

die perspektive Verzerrung verursacht in den Bildern unterschiedlich abgebildete geometrische Formen eines Oberflächenausschnitts
Verdeckungen führen dazu, dass der korrespondierende Punkt unauffindbar wird
Unterschiede in den Beleuchtungsverhältnissen (Helligkeits- und Kontrastunterschied) können die Zuordnung ebenfalls erschweren
die unterschiedliche Perspektive führt außerdem zu Unterschieden in der Reflektanz in Richtung der Kamera des auf die Oberfläche auftreffenden Lichtes
sich wiederholende Muster kann zu falsch zugeordneten Bildpunkten führen

Entsprechend gibt es eine Vielzahl an ganz unterschiedlichen Methoden. Man unterscheidet grauwertbasierte (flächenhafte) von merkmalsbasierten Verfahren. Die flächenhaften Verfahren untersuchen kleine Bildausschnitte und vergleichen die jeweiligen Grauwerte (Helligkeitswerte). Die merkmalsbasierten Verfahren extrahieren zunächst Merkmale (z. B. Eckpunkte) und gleichen darauf aufbauende Merkmalsvektoren ab.

Stereo-Bild-Verarbeitung

Epipolargeometrie

Die Epipolargeometrie beschreibt die Abbildungsgeometrie eines 3D-Objektpunktes in einem Stereobildpaar. Die Beziehung zwischen den Bildkoordinaten korrespondierender Punkte wird durch eine Fundamentalmatrix beschrieben. Mit ihr lässt sich zu einem gegebenen Punkt im ersten Bild die dazugehörige Epipolarlinie im zweiten Bild bestimmen, auf der sich der korrespondierende Bildpunkt befindet.

Man kann die Fundamentalmatrix aus einer Anzahl an korrespondierenden Bildpunkten schätzen. Dazu existieren zwei weit verbreitete Berechnungsmethoden: der minimale 7-Punkt-Algorithmus und der 8-Punkt-Algorithmus.

Bildsequenz-Verarbeitung (Struktur aus Bewegung)

Aufbauend auf diese verteilten Bildpunktpaare (sparse image matching) ist es möglich die Fundamentalmatrix zu schätzen, um die gegenseitige relative Orientierung der Bilder zu bestimmen. Dem folgt i. d. R. eine dichte Korrespondenzsuche (dense image matching). Alternativ werden auch mit Hilfe globaler Optimierungsverfahren die korrespondierenden Punkte geschätzt.

Shape-from-X

Shape-from-Stereo

Bei der Stereo-Rekonstruktion werden zwei Bilder von jeweils unterschiedlichen Blickpunkten aus verwendet. Als Vorbild dient das menschliche räumliche Sehen (stereoskopisches Sehen). Kennt man die gegenseitige relative Orientierung eines Bildpaars, dann kann man korrespondierende Bildpunktpaare dazu verwenden, um die ursprünglichen 3D-Objektpunkte mittels Triangulation zu berechnen. Das Schwierige daran ist die Korrespondenzsuche, insbesondere für Oberflächen mit wenig Textur oder verdeckte Gebiete.^[10]

Shape-from-Silhouette / Shape-from-Contour

Bei diesem Verfahren benutzt man mehrere Bilder, welche das Objekts aus unterschiedlichen Richtungen abbilden, um aus deren äußeren Umriss (die Silhouette) seine geometrische Form abzuleiten. Bei diesem Verfahren wird die Kontour aus einem groben Volumen quasi herausgeschnitten, so ähnlich wie ein Bildhauer eine Büste aus einem groben Holzklotz herausschnitzt. Im englischen Sprachgebrauch wird hierbei auch von Shape-from-Contour oder Space-Carving gesprochen.

Voraussetzung für diese Technik ist, dass man das zu bestimmende Objekt (Vordergrund) vom Hintergrund trennen kann. Dabei kommen Techniken zur Bildsegmentierung zum Einsatz. Das Ergebnis wird dann als Representation eines Volumens mittels Voxel dargestellt und wird auch visuelle Hülle (auf Englisch: visual hull) genannt.^[10]

Shape-from-Shading / Photometric Stereo

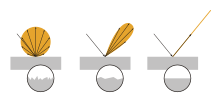
Diese Methode versucht die Form eines Objekts anhand seiner Schattierung zu bestimmen. Sie beruht auf zwei Effekten: erstens ist die Reflexion von auf eine Oberfläche auftreffender paralleler Strahlung abhängig von der Oberflächennormalen und der Beschaffenheit (insbesondere Rauigkeit) der Oberfläche, und zweitens ist die vom Betrachter (Kamera) gesehene Helligkeit abhängig von der Perspektive, genauer gesagt vom Winkel unter dem man die Oberfläche betrachtet.

Bei einer Reflexion an einer rauen Oberfläche spricht man von diffuser Reflexion, welche durch das Lambertsche Kosinusgesetz beschrieben wird (s. Abb. Links). Die Richtung der Beleuchtungsquelle spielt dabei nur insofern eine Rolle, dass die gesamte Strahlungsenergie verringert wird, abhängig vom Einfallswinkel. Die Reflexion (der Ausfallwinkel) ist jedoch völlig unabhängig vom Einfallswinkel, sie ist lediglich abhängig vom Winkel zur Oberflächennormalen. Unter der Annahme der diffusen Reflexion ist die zum Betrachter (Kamera) reflektierte Strahlung deshalb nur abhängig vom Kosinus des Winkels zur Oberflächennormalen. Dies lässt sich vorteilhaft nutzen, wenn man die Beleuchtungsstärke kennt, um die Richtung der Oberflächennormalen zu berechnen.

Shape-from-Motion / Optischer Fluss

Beim optischen Fluss wird eine Sequenz von Bildern untersucht, ob und wie sich die Bilder (bzw. die Kamera) bewegt hat. Dazu werden lokale Helligkeitsänderungen zwischen benachbarten Bildern untersucht. Dazu kommen verschiedene Methoden zur Merkmalsextraktion zum Einsatz und Verfahren zur Korrespondenzanalyse, um korrespondierende Punkte zu identifizieren. Die Differenz zwischen diesen korrespondierenden Punkten entspricht dann der lokalen Bewegung.

Gestützt auf diese Punkte ist es möglich die Objektform durch 3D-Rekonstruktion zu bestimmen (s. Abschnitt 'Struktur aus Bewegung'). Aufgrund der Verwendung nur weniger Punkte ist das Ergebnis jedoch sehr grob und eignet sich lediglich zur Erkennung von Hindernissen, um so die Navigation zu unterstützen. Für eine genaue 3D-Modellierung ist es jedoch ungeeignet.

Shape-from-Texture

Kennt man die auf einer Oberfläche aufgetragene Textur, z. B. ein Stück Stoff mit einem sich wiederholenden Muster, dann ändert sich das Muster aufgrund lokaler Unebenheiten. Genauer gesagt der Winkel, unter dem man die Oberfläche (und damit Oberflächennormale) betrachtet, ändert sich und verzerrt somit die sichtbare geometrische Form der Textur. In dieser Hinsicht ähnelt dieses Verfahren dem Shape-from-Shading. Es sind viele Schritte notwendig um die Form ableiten zu können inklusive der Extraktion der wiederholenden Muster, die Messung lokaler Frequenzen um lokale affine Deformationen zu berechnen und schließlich die lokale Orientierung der Oberfläche abzuleiten.^[1]^[3]^[11]

Im Gegensatz zum Lichtstreifenverfahren (s. Abschnitt Strukturiertes codiertes Licht) ist die Textur real auf der Oberfläche vorhanden und wird nicht durch einen Projektor künstlich erzeugt.

Strukturiertes codiertes Licht

Ersetzt man bei einem Stereo-Kamerasystem eine Kamera durch einen Projektor, welcher strukturiertes (codiertes) Licht aussendet, kann man ebenfalls eine Triangulation durchführen und somit die dreidimensionale Form des Objekts rekonstruieren. Das strukturierte Licht erzeugt eine bekannte Textur, welche auf der Oberfläche durch das Relief verzerrt abgebildet wird. Die Kamera „erkennt“ anhand dieser Textur die jeweilige lokale codierte Struktur und kann durch Strahlenschnitt die 3D-Position berechnen (s. auch Streifenlichtscanning und Lichtschnittverfahren).^[10] Irrtümlicherweise wird dies manchmal gleichgesetzt mit Shape-from-Textur.

Shape-from-(De-)Focus

Die Linsengleichung beschreibt die prinzipielle Abbildung eines Objektpunktes und seines scharf abgebildeten Bildpunktes für eine Kamera mit einem Objektiv (s. geometrische Optik). Der Durchmesser der Unschärfe verhält sich proportional zur Änderung der Fokuseinstellung (entspricht der Änderung der Bildweite). Unter der Voraussetzung, dass die Distanz zum Objekt fixiert ist, kann damit – aus einer Reihe von unscharfen Bildern und Messung des Durchmessers von unscharf abgebildeten Punkten – die Gegenstandsweite (entspricht der Distanz zum Objekt) berechnet werden.^[12]

Aktive und sonstige Sensoren

LiDAR

LiDAR (light detection and ranging, auf Deutsch: Licht Detektion und Entfernungsmessung) ist ein aktives Verfahren zur berührungslosen Entfernungsmessung. Das Messprinzip beruht auf der Messung der Laufzeit eines ausgesendeten Lasersignal. Dieses Verfahren wird unter anderem in der Robotik zur Navigation eingesetzt.

3D-TOF-Kamera

Eine 3D-ToF-Kamera (time of flight, auf Deutsch: Laufzeit) ist eine Kamera mit einem aktiven Sensor. Der Unterschied zu anderen Verfahren wie Laserscanning oder Lidar ist, dass es ein flächenhafter Sensor ist. Ähnlich wie bei einer normalen Digitalkamera enthält die Bildebene gleichmäßig angeordnete Lichtsensoren und zusätzlich winzige LEDs (oder Laserdioden), die einen infraroten Lichtpuls aussenden. Das von der Oberfläche reflektierte Licht wird von der Optik eingefangen und auf den Sensor abgebildet. Ein Filter sorgt dafür, dass nur die ausgestrahlte Farbe durchgelassen wird. Dies ermöglicht die gleichzeitige Entfernungsbestimmung eines Oberflächenstücks. Es kommt bei der autonomen Navigation zur Objekterkennung zum Einsatz.

Kinect

Kinect ist ein Kamerasystem mit strukturiertem Licht zur Objektrekonstruktion.

Omnidirektionale Kameras

Eine omnidirektionale Kamera ist in der Lage aus allen Richtungen (360°) ein Bild aufzunehmen. Dies wird meist durch eine Kamera erreicht, welche auf einen konischen Spiegel ausgerichtet ist und somit die vom Spiegel reflektierte Umgebung aufgenommen wird. Je nach Ausrichtung ist es somit möglich mit nur einer Aufnahme ein vollständiges horizontales oder vertikales Rundumbild aufzunehmen.

Weitere Methoden

SLAM

Als SLAM (englisch Simultaneous Localization and Mapping; deutsch Simultane Positionsbestimmung und Kartenerstellung) wird ein Verfahren bezeichnet, welches vor allem zur autonomen Navigation eingesetzt wird. Dabei ist ein mobiler Roboter mit verschiedenen Sensoren ausgerüstet, um seine Umgebung dreidimensional zu erfassen. Das besondere an diesem Verfahren ist, dass die Positionsbestimmung und die Kartenerstellung gleichzeitig durchgeführt werden. Die Bestimmung der absoluten Position ist eigentlich nur möglich, wenn man bereits eine Karte hat und anhand von Landmarken, die der Roboter identifiziert, dessen Lage innerhalb der Karte bestimmen kann. Oftmals sind die Karten jedoch nicht detailliert genug, weswegen ein mobiler Roboter keine – in der Karte vorhandene – Landmarken finden kann. Darüber hinaus ist die Identifikation solcher Landmarken äußerst schwierig, weil die Perspektive einer Karte eine völlig andere ist, als die Perspektive des Roboters.^[13] Mit SLAM versucht man solche Problemstellungen zu lösen.

Anwendungen

In industriellen Umgebungen werden die Techniken des maschinellen Sehens heutzutage erfolgreich eingesetzt. Computer unterstützen beispielsweise die Qualitätskontrolle und vermessen einfache Gegenstände. Weitgehend bestimmt der Programmierer hier die Umgebungsbedingungen, die wichtig für ein fehlerfreies Ablaufen seiner Algorithmen sind (Kameraposition, Beleuchtung, Geschwindigkeit des Fließbandes, Lage der Objekte usw.).

Beispiele für den Einsatz in industriellen Umgebungen sind:

Auf einem Förderband werden Beilegscheiben kontrolliert, um die Maßhaltigkeit zu überprüfen und die Fehlerquote des Endprodukts um mehrere Zehnerpotenzen zu verkleinern.
Schweißroboter werden an die richtige Schweißposition gesteuert.

In natürlichen Umgebungen werden weit schwierigere Anforderungen an die Techniken im Computer Vision gestellt. Hier hat der Programmierer keinen Einfluss auf die Umgebungsbedingungen, was die Erstellung eines robusten, fehlerfrei ablaufenden Programms erheblich erschwert. Man kann sich dieses Problem anhand eines Beispiels zur Erkennung von Automobilen verdeutlichen: Ein schwarzes Auto hebt sich vor einer weißen Wand gut ab, der Kontrast zwischen einem grünen Auto und einer Wiese ist allerdings sehr gering und eine Unterscheidung nicht einfach.

Beispiele für den Einsatz in natürlichen Umgebungen sind:

die autonome Navigation von Fahrzeugen
Erkennung von menschlichen Gesichtern und deren Mimik
Erkennung von Personen und deren Tätigkeit

Weitere Anwendungen finden sich in einer Vielzahl unterschiedlicher Bereiche:

Automatisierung
Berührungslose 1D-, 2D- und 3D-Vermessung (Photogrammetrie) und Qualitätskontrolle
Gestenerkennung
Medizintechnik
Personenerkennung (Gesichtserkennung, Mimikerkennung, Biometrie)
Robotersehen
Zeichen- und Schrifterkennung (OCR, Handschrifterkennung)

Maschinelles Sehen

Maschinelles Sehen umfasst alle industriellen Anwendungen, bei denen, basierend auf visuellen Systemen, automatisierte Prozesse gelenkt werden. Typische Einsatzgebiete sind industrielle Herstellungsprozesse, die Automatisierungstechnik und die Qualitätssicherung. Weitere Einsatzgebiete finden sich z. B. in der Verkehrstechnik – von der einfachen Radarfalle bis hin zum „sehenden Fahrzeug“ – und in der Sicherheitstechnik (Zutrittskontrolle, automatische Erkennung von Gefahrensituationen). Dabei werden Methoden aus dem Fachgebiet Computer Vision eingesetzt.

Die Technologien und Methoden die hierbei zum Einsatz kommen, müssen speziellen Anforderungen genügen, welche sich im industriellen Umfeld ergeben. Industrielle visuelle Systeme erfordern eine hohe Zuverlässigkeit, Stabilität und müssen besonders robust sein. Insofern versucht maschinelles Sehen existierende Technologien auf neue Art und Weise anzuwenden und zu integrieren.

Folgende Aufgabenstellungen können derzeit wirtschaftlich sinnvoll gelöst werden:

Produktkontrolle durch automatische optische Inspektion
Defekterkennung unter Oberflächen
Form- und Maßprüfung
Lageerkennung
Oberflächeninspektion
Objekterkennung
Schichtdickenmessungen
Vollständigkeitsprüfung

Einzelnachweise

↑ ^a ^b David A. Forsyth, Jean Ponce: Computer Vision: A Modern Approach. 2. Auflage. 2012, Pearson Education, Prentice Hall 2012, ISBN 978-0-13-608592-8.
↑ Reinhard Klette: Concise Computer Vision - An Introduction into Theory and Algorithms. Springer-Verlag, London 2014, ISBN 978-1-4471-6319-0, doi:10.1007/978-1-4471-6320-6
↑ ^a ^b Richard Szeliski: Computer Vision - Algorithms and Applications. Springer-Verlag, London 2011, ISBN 978-1-84882-934-3, doi:10.1007/978-1-84882-935-0 (szeliski.org)
↑ ^a ^b Richard Szeliski: Computer Vision (= Texts in Computer Science). Springer London, London 2011, ISBN 978-1-84882-934-3, doi:10.1007/978-1-84882-935-0.
↑ Karl Kraus: Photogrammetrie. 6. Auflage. Band 1: Grundlagen und Standardverfahren. Dümmler, Bonn 1997, ISBN 3-427-78646-3.
↑ Ludwig Seidel: Ueber die Theorie der Fehler, mit welchen die durch optische Instrumente gesehenen Bilder behaftet sind, und über die mathematischen Bedingungen ihrer Aufhebung. In: Königliche Bayerische Akademie der Wissenschaften in München (Hrsg.): Abhandlungen der naturwissenschaftlich-technischen Commission. Band 1. München 1857, S. 227–267 (OPACplus Bayerische Staatsbibliothek).
↑ ^a ^b J. Chris McGlone, Edward M Mikhail, James S Bethel, Roy Mullen, American Society for Photogrammetry and Remote Sensing: Manual of photogrammetry. 5. Auflage. American Society for Photogrammetry and Remote Sensing, Bethesda, Md. 2004, ISBN 1-57083-071-1.
↑ Thomas Luhmann: Nahbereichsphotogrammetrie. Wichmann, Heidelberg 2003, ISBN 3-87907-398-8.
↑ Volker Rodehorst: Photogrammetrische 3D-Rekonstruktion im Nahbereich durch Auto-Kalibrierung mit projektiver Geometrie. Wiss. Verlag, Berlin 2004, ISBN 3-936846-83-9.
↑ ^a ^b ^c Anke Bellmann, Olaf Hellwich, Volker Rodehorst, Yilmaz Ulas: A Benchmark Dataset for Performance Evaluation of Shape-from-X Algorithms. In: The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Vol. XXXVII. Part B3b. Beijing Juli 2008, S. 67–72 (englisch, isprs.org [PDF; abgerufen am 6. Juni 2020] isprs.org).
↑ Shape from Texture. Abgerufen am 23. Februar 2021.
↑ Tobias Dierig: Gewinnung von Tiefenkarten aus Fokusserien. 2002, abgerufen am 6. Juni 2020.
↑ Rongxing Li, Kaichang Di, Larry H. Matthies, William M. Folkner, Raymond E. Arvidson: Rover Localization and Landing-Site Mapping Technology for the 2003 Mars Exploration Rover Mission. Januar 2004, abgerufen am 11. Juni 2020 (englisch).

Literatur

Richard Hartley, Andrew Zisserman: Multiple View Geometry in Computer Vision. 2. Auflage. Cambridge University Press, Cambridge 2004, ISBN 0-521-54051-8.
Carsten Steger, Markus Ulrich, Christian Wiedemann: Machine Vision Algorithms and Applications. 2. Auflage. Wiley-VCH, Weinheim 2018, ISBN 978-3-527-41365-2 (wiley.com).

Weblinks

Commons: Computer Vision – Sammlung von Bildern, Videos und Audiodateien

Fraunhofer-Allianz Vision, Bildverarbeitung – Lösungen für maschinelles Sehen

[:2-1] David A. Forsyth, Jean Ponce: Computer Vision: A Modern Approach. 2. Auflage. 2012, Pearson Education, Prentice Hall 2012, ISBN 978-0-13-608592-8.

[2] Reinhard Klette: Concise Computer Vision - An Introduction into Theory and Algorithms. Springer-Verlag, London 2014, ISBN 978-1-4471-6319-0, doi:10.1007/978-1-4471-6320-6

[:3-3] Richard Szeliski: Computer Vision - Algorithms and Applications. Springer-Verlag, London 2011, ISBN 978-1-84882-934-3, doi:10.1007/978-1-84882-935-0 (szeliski.org)

[:0-4] Richard Szeliski: Computer Vision (= Texts in Computer Science). Springer London, London 2011, ISBN 978-1-84882-934-3, doi:10.1007/978-1-84882-935-0.

[5] Karl Kraus: Photogrammetrie. 6. Auflage. Band 1: Grundlagen und Standardverfahren. Dümmler, Bonn 1997, ISBN 3-427-78646-3.

[6] Ludwig Seidel: Ueber die Theorie der Fehler, mit welchen die durch optische Instrumente gesehenen Bilder behaftet sind, und über die mathematischen Bedingungen ihrer Aufhebung. In: Königliche Bayerische Akademie der Wissenschaften in München (Hrsg.): Abhandlungen der naturwissenschaftlich-technischen Commission. Band 1. München 1857, S. 227–267 (OPACplus Bayerische Staatsbibliothek).

[:4-7] J. Chris McGlone, Edward M Mikhail, James S Bethel, Roy Mullen, American Society for Photogrammetry and Remote Sensing: Manual of photogrammetry. 5. Auflage. American Society for Photogrammetry and Remote Sensing, Bethesda, Md. 2004, ISBN 1-57083-071-1.

[8] Thomas Luhmann: Nahbereichsphotogrammetrie. Wichmann, Heidelberg 2003, ISBN 3-87907-398-8.

[9] Volker Rodehorst: Photogrammetrische 3D-Rekonstruktion im Nahbereich durch Auto-Kalibrierung mit projektiver Geometrie. Wiss. Verlag, Berlin 2004, ISBN 3-936846-83-9.

[:1-10] Anke Bellmann, Olaf Hellwich, Volker Rodehorst, Yilmaz Ulas: A Benchmark Dataset for Performance Evaluation of Shape-from-X Algorithms. In: The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Vol. XXXVII. Part B3b. Beijing Juli 2008, S. 67–72 (englisch, isprs.org [PDF; abgerufen am 6. Juni 2020] isprs.org).

[11] Shape from Texture. Abgerufen am 23. Februar 2021.

[12] Tobias Dierig: Gewinnung von Tiefenkarten aus Fokusserien. 2002, abgerufen am 6. Juni 2020.

[13] Rongxing Li, Kaichang Di, Larry H. Matthies, William M. Folkner, Raymond E. Arvidson: Rover Localization and Landing-Site Mapping Technology for the 2003 Mars Exploration Rover Mission. Januar 2004, abgerufen am 11. Juni 2020 (englisch).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]