Informatik

• 
• 
• 
• 

Informatik ist die Wissenschaft von der systematischen Darstellung, Speicherung, Verarbeitung und Übertragung von Informationen, wobei in der Regel die automatische Verarbeitung mit Computern betrachtet wird. Sie ist zugleich Grundlagen- und Formalwissenschaft als auch Ingenieurdisziplin.

Geschichte der Informatik

Etymologie

Das Wort Informatik entstand durch das Anhängen des Suffix -ik an den Wortstamm von Information. Karl Steinbuch prägte die Bezeichnung Informatik zusammen mit Helmut Gröttrup und verwendete sie in seiner ersten Publikation „Informatik: Automatische Informationsverarbeitung“ im April 1957, die er bei Standard Elektrik AG (SEG) veröffentlichte. Um die Bedeutung der Automation oder Mathematik für die Informatik zu betonen, wird Informatik manchmal auch als Kofferwort aus Information und Automatik oder Information und Mathematik ausgegeben.

Nach einem internationalen Kolloquium in Dresden am 26. Februar 1968 setzte sich Informatik als Bezeichnung für die Wissenschaft nach französischem (informatique) und russischem Vorbild (Информатика) auch im deutschen Sprachraum durch. Im Juli desselben Jahres wurde der Begriff Informatik erstmals als deutscher Name für ein neu einzurichtendes Studienfach in einer Berliner Rede des Bundesministers Gerhard Stoltenberg verwendet. Während im englischen Sprachraum die Bezeichnung Computer Science üblich ist, konnte sich die deutsche Entsprechung Computerwissenschaften nicht durchsetzen. Jedoch wird der Ausdruck Informatics im Englischen für bestimmte Teile der Angewandten Informatik verwendet – etwa im Falle der Bioinformatics oder der Geoinformatics. Bei Übersetzungen ins Englische wird im deutschen Sprachraum teilweise die Bezeichnung Informatics gegenüber Computer Science bevorzugt.

Entwicklungen in den deutschsprachigen Ländern

Bereits Gottfried Wilhelm Leibniz hatte sich mit binären Zahlendarstellungen beschäftigt. Gemeinsam mit der Booleschen Algebra, die zuerst 1847 von George Boole ausgearbeitet wurde, bilden sie die wichtigsten mathematischen Grundlagen späterer Rechensysteme. Die Anfänge der modernen Informatik gehen in Deutschland bis ins Jahr 1952 zurück, als im Juli an der RWTH Aachen die erste deutsche Informatik-Tagung zum Thema programmgesteuerte Rechengeräte und Integrieranlagen mit Konrad Zuse und Heinz Nixdorf stattfand. 1953 folgte ein Kolloquium zu Rechenanlagen in Göttingen, nachdem dort der erste deutsche Elektronenrechner, die G1, in Betrieb ging. Die TU München entwickelte unter Leitung von Hans Piloty und Robert Sauer ebenfalls einen Röhrenrechner, die PERM, die 1956 in Betrieb ging, und lud 1954 zu einem Rundtischgespräch ein. Am Institut für praktische Mathematik (IPM) der Technischen Hochschule Darmstadt (TH Darmstadt), das der Mathematiker Alwin Walther seit 1928 aufbaute, konnten sich dann 1956 die ersten Studenten am Darmstädter Elektronischen Rechenautomaten mit den Problemen von Rechenautomaten befassen. Zeitgleich wurden an der TH Darmstadt die ersten Programmiervorlesungen- und praktika angeboten. Aufgrund des Renommees, das die TH Darmstadt zu dem Zeitpunkt in der Rechenautomatenforschung hatte, fand ein Kongress zum Fachgebiet Informatik (elektronische Rechenmaschinen und Informationsverarbeitung) mit internationaler Beteiligung im Oktober 1955 an der TH Darmstadt statt, der als Geburtsstätte der Programmiersprache ALGOL gilt.

Der Bundesausschuss für wissenschaftliche Forschung verabschiedete am 26. April 1967 das Programm für die Förderung der Forschung und Entwicklung auf dem Gebiet der Datenverarbeitung für öffentliche Aufgaben. Für die Umsetzung war der sogenannte „Fachbeirat für Datenverarbeitung“ zuständig, der überwiegend aus Vertretern der Hochschulen und außeruniversitären Forschungseinrichtungen bestand. Auf der siebten Sitzung des Fachbeirates am 15. November 1967 signalisierte Karl Ganzhorn, der zu dem Zeitpunkt für Forschung und Entwicklung bei IBM Deutschland zuständig war, die Probleme der Industrie, Fachpersonal zu finden. Der Direktor des Instituts für Nachrichtenverarbeitung an der TH Darmstadt, Robert Piloty, wies darauf hin, dass die deutschen Hochschulen dafür zuständig seien, qualifiziertes Personal auszubilden. Daraufhin bildete sich der Ausschuss „DV-Lehrstühle und -Ausbildung“. Den Vorsitz übernahm Piloty. Der Ausschuss formulierte Empfehlungen für die Ausbildung von Informatikern, welche die Einrichtung eines Studiengangs der Informatik an mehreren Universitäten und Technischen Hochschulen vorsahen.

1967 bot die TU München mit dem Studienzweig Informationsverarbeitung den ersten Informatikstudiengang in Deutschland im Rahmen des Mathematikstudiums auf Initiative Friedrich Ludwig Bauers an. 1968 führte die TH Darmstadt einen Studienplan „Informatik“ an der Fakultät für Elektrotechnik ein. 1969 folgte der Studiengang „Datentechnik (Technische Informatik)“ des Fachbereiches Regulierungs- und Datentechnik und 1970 ein Mathematikstudiengang, der mit dem Grad „Diplomingenieur im Fach Mathematik mit Schwerpunkt Informatik“ abschloss. Am 1. September 1969 begann die Technische Universität Dresden als erste Hochschule der DDR mit der Ausbildung von Dipl.-Ing. für Informationsverarbeitung. Ebenfalls 1969 begann die Ingenieurschule Furtwangen (später Fachhochschule Furtwangen) mit der Ausbildung, hier noch Informatorik genannt. Im Wintersemester 1969/70 bot die Universität Karlsruhe (heute Karlsruher Institut für Technologie) als erste bundesdeutsche Hochschule ein Informatikstudium an, der mit dem Grad „Diplom-Informatiker“ abschloss.

Die Johannes Kepler Universität (JKU) Linz startete im Wintersemester 1969/70 als erste österreichische Universität mit der Studienrichtung Informatik und der Ausbildung zum Diplomingenieur. Im Wintersemester 1970/71 folgte die Technische Universität Wien. Wenige Jahre darauf gründeten sich die ersten Fakultäten für Informatik.

Entwicklungen in den USA und in Großbritannien

1937 veröffentlichte der Brite Alan Turing seine Arbeit On Computable Numbers with an application to the Entscheidungsproblem, in welcher die nach ihm benannte Turingmaschine vorgestellt wird, ein mathematisches Maschinenmodell, das bis heute für die Theoretische Informatik von größter Bedeutung ist. Dem Begriff der Berechenbarkeit liegen bis heute universelle Modelle, wie die Turingmaschine und die Komplexitätstheorie zu Grunde, die sich ab den 1960er Jahren zu entwickeln begann. Die Berechenbarkeit greift bis in die Gegenwart auf Varianten dieser Modelle zurück.

In englischsprachigen Ländern wird die Einzelwissenschaft als computer science bezeichnet. Der erste universitäre Abschluss war das Diploma in Numerical Analysis and Automatic Computing an der britischen University of Cambridge. Das einjährige postgraduale Studium konnte ab Oktober 1953 aufgenommen werden. Seit 1962 bestand an der Purdue University in den USA ein Department of Computer Science.

Organisationen und Turing Award

Die Gesellschaft für Informatik (GI) wurde 1969 gegründet und ist die größte Fachvertretung im deutschsprachigen Raum. International bedeutend sind vor allem die beiden großen amerikanischen Vereinigungen Association for Computing Machinery (ACM) seit 1947 und das Institute of Electrical and Electronics Engineers (IEEE) seit 1963. Die bedeutendste deutschsprachige Organisation, die sich mit ethischen und gesellschaftlichen Effekten der Informatik auseinandersetzt, ist das Forum InformatikerInnen für Frieden und gesellschaftliche Verantwortung. Die Association for Computing Machinery vergibt jährlich den Turing Award, der vom Rang her in der Informatik vergleichbar mit dem Nobelpreis ist.

Rechenmaschinen – Vorläufer des Computers

Ein japanischer Soroban

Als erste Vorläufer der Informatik jenseits der Mathematik können die Bestrebungen angesehen werden, zwei Arten von Maschinen zu entwickeln: solche, mit deren Hilfe mathematische Berechnungen ausgeführt oder vereinfacht werden können („Rechenmaschinen“), und solche, mit denen logische Schlüsse gezogen und Argumente überprüft werden können („Logische Maschinen“). Als einfache Rechengeräte leisteten Abakus und später der Rechenschieber unschätzbare Dienste. 1641 konstruierte Blaise Pascal eine mechanische Rechenmaschine, die Additionen und Subtraktionen inklusive Überträgen durchführen konnte. Nur wenig später stellte Gottfried Wilhelm Leibniz eine Rechenmaschine vor, die alle vier Grundrechenarten beherrschte. Diese Maschinen basieren auf ineinandergreifenden Zahnrädern. Einen Schritt in Richtung größerer Flexibilität ging ab 1838 Charles Babbage, der eine Steuerung der Rechenoperationen mittels Lochkarten anstrebte. Erst Herman Hollerith war dank dem technischen Fortschritt ab 1886 in der Lage, diese Idee gewinnbringend umzusetzen. Seine auf Lochkarten basierenden Zählmaschinen wurden unter anderem bei der Auswertung einer Volkszählung in den USA eingesetzt.

Die Geschichte der logischen Maschinen wird oft bis ins 13. Jahrhundert zurückverfolgt und auf Ramon Llull zurückgeführt. Auch wenn seine rechenscheibenähnlichen Konstruktionen, bei denen mehrere gegeneinander drehbare Scheiben unterschiedliche Begriffskombinationen darstellen konnten, mechanisch noch nicht sehr komplex waren, war er wohl derjenige, der die Idee einer logischen Maschine bekannt gemacht hat. Von diesem sehr frühen Vorläufer abgesehen, verläuft die Geschichte logischer Maschinen eher sogar zeitversetzt zu jener der Rechenmaschinen: Auf 1777 datiert ein rechenschieberähnliches Gerät des dritten Earl Stanhope, dem zugeschrieben wird, die Gültigkeit von Syllogismen (im aristotelischen Sinn) zu prüfen. Eine richtige „Maschine“ ist erstmals in der Gestalt des „Logischen Pianos“ von Jevons für das späte 19. Jahrhundert überliefert. Nur wenig später wurde die Mechanik durch elektromechanische und elektrische Schaltungen abgelöst. Ihren Höhepunkt erlebten die logischen Maschinen in den 1940er und 1950er Jahren, zum Beispiel mit den Maschinen des englischen Herstellers Ferranti. Mit der Entwicklung universeller digitaler Computer nahm – im Gegensatz zu den Rechenmaschinen – die Geschichte selbständiger logischen Maschinen ein jähes Ende, indem die von ihnen bearbeiteten und gelösten Aufgaben zunehmend in Software auf genau jenen Computern realisiert wurden, zu deren hardwaremäßigen Vorläufern sie zu zählen sind.

Entwicklung moderner Rechenmaschinen

Siehe auch: Der Siegeszug des elektronischen Digitalrechners im Artikel Computer

Konrad Zuse

Eine der ersten größeren Rechenmaschinen ist die von Konrad Zuse erstellte, noch immer rein mechanisch arbeitende Z1 von 1937. Zu dieser Zeit waren in großen Verwaltungen Tabelliermaschinen die herrschende Technik, wobei Zuse der Einsatz im Ingenieursbereich vorschwebte. Vier Jahre später realisierte Zuse seine Idee mittels elektrischer Relais: Die Z3 von 1941 trennte als weltweit erster funktionsfähiger frei programmierbarer Digitalrechner bereits Befehls- und Datenspeicher und Ein-/Ausgabepult.

Etwas später wurden in England die Bemühungen zum Bau von Rechenmaschinen zum Entschlüsseln von deutschen militärischen Geheimbotschaften unter maßgeblicher Leitung von Alan Turing (Turingbombe) und von Thomas Flowers (Colossus) mit großem Erfolg vorangetrieben. Parallel entwickelte Howard Aiken mit Mark I (1944) den ersten programmgesteuerten Relaisrechner der USA, wo die weitere Entwicklung maßgeblich vorangetrieben wurde. Weitere Relaisrechner entstanden in den Bell-Labors (George Stibitz). Als erster Röhrenrechner gilt der Atanasoff-Berry-Computer. Einer der Hauptakteure ist hier John von Neumann, nach dem die bis heute bedeutende Von-Neumann-Architektur benannt ist. 1946 erfolgte die Entwicklung des Röhrenrechners ENIAC, 1949 wurde der EDSAC gebaut – mit erstmaliger Implementation der Von-Neumann-Architektur.

Ab 1948 stieg IBM in die Entwicklung von Computern ein und wurde innerhalb von zehn Jahren Marktführer. Einen Meilenstein in der Firmengeschichte stellte 1964 die Einführung des System/360 dar. Der Großrechner ist der Urahn der heutigen Z-Systems-Mainframes und folgte zeitlich den IBM 700/7000-Serien. Bereits 1959 wurde mit der IBM 1401 ein Rechner auch für mittelgroße Unternehmen eingeführt, der oftmals wegen seiner Verkaufszahlen als der Ford Modell T der Computerindustrie bezeichnet wird. Mit der Entwicklung der Transistortechnik und der Mikroprozessortechnik wurden Computer immer leistungsfähiger und preisgünstiger. Im Jahre 1982 öffnete die Firma Commodore schließlich mit dem C64 den Massenmarkt speziell für Heimanwender, aber auch weit darüber hinaus.

Programmiersprachen

→ Hauptartikel: Programmiersprachen

Konrad Zuse entwickelte bereits während des Zweiten Weltkriegs zwischen 1942 und 1945 die höhere Programmiersprache Plankalkül, die niemals praktisch eingesetzt wurde. Bedeutsam für die Entwicklung der Programmiersprachen war die Erfindung der „automatischen Programmierung“ durch Heinz Rutishauser (1951). 1956 beschrieb Noam Chomsky eine Hierarchie formaler Grammatiken, mit denen formale Sprachen und jeweils spezielle Maschinenmodelle korrespondieren. Diese Formalisierungen erlangten für die Entwicklung der Programmiersprachen große Bedeutung. Wichtige Meilensteine waren die Entwicklung von Fortran (aus Englisch: „FORmula TRANslation“, Formelübersetzung; erste höhere Programmiersprache, 1957), ALGOL (aus englisch: „ALGOrithmic Language“, Algorithmensprache; strukturiert/imperativ; 1958/1960/1968), Lisp (aus englisch: „LISt Processing“, Verarbeitung von Listen; funktional, 1959), COBOL (aus englisch: „COmmon Business Orientated Language“, Programmiersprache für kaufmännische Anwendungen, 1959), Smalltalk (objektorientiert, 1971), Prolog (logisch, 1972) und SQL (Relationale Datenbanken, 1976). Einige dieser Sprachen stehen für typische Programmierparadigmen ihrer jeweiligen Zeit. Weitere über lange Zeit in der Praxis eingesetzte Programmiersprachen sind BASIC (seit 1960), C (seit 1970), Pascal (seit 1971), Objective-C (objektorientiert, 1984), C++ (objektorientiert, generisch, multi-paradigma, seit 1985), Java (objektorientiert, seit 1995) und C# (objektorientiert, um 2000). Sprachen und Paradigmenwechsel wurden von der Informatik-Forschung intensiv begleitet oder vorangetrieben.

Wie bei anderen Wissenschaften gibt es auch einen zunehmenden Trend zur Spezialisierung.

Disziplinen der Informatik

Alan-Turing-Gedenkstatue im Sackville Park in Manchester

Die Informatik unterteilt sich in die Teilgebiete der Theoretischen Informatik, der Praktischen Informatik und der Technischen Informatik.

Die Anwendungen der Informatik in den verschiedenen Bereichen des täglichen Lebens sowie in anderen Fachgebieten, wie beispielsweise der Wirtschaftsinformatik, Geoinformatik und Medizininformatik werden unter dem Begriff der Angewandten Informatik geführt. Auch die Auswirkungen auf die Gesellschaft werden interdisziplinär untersucht.

Architektur der Informatik

Die Theoretische Informatik bildet die theoretische Grundlage für die anderen Teilgebiete. Sie liefert fundamentale Erkenntnisse für die Entscheidbarkeit von Problemen, für die Einordnung ihrer Komplexität und für die Modellierung von Automaten und Formalen Sprachen.

Auf diese Erkenntnisse stützen sich Disziplinen der Praktischen und der Technischen Informatik. Sie beschäftigen sich mit zentralen Problemen der Informationsverarbeitung und suchen anwendbare Lösungen.

Die Resultate finden schließlich Verwendung in der Angewandten Informatik. Diesem Bereich sind Hardware- und Software-Realisierungen zuzurechnen und damit ein Großteil des kommerziellen IT-Marktes. In den interdisziplinären Fächern wird darüber hinaus untersucht, wie die Informationstechnik Probleme in anderen Wissenschaftsgebieten lösen kann, wie beispielsweise die Entwicklung von Geodatenbanken für die Geographie, aber auch die Wirtschafts- oder Bioinformatik.

Theoretische Informatik

→ Hauptartikel: Theoretische Informatik

Als Rückgrat der Informatik befasst sich das Gebiet der Theoretischen Informatik mit den abstrakten und mathematikorientierten Aspekten der Wissenschaft. Das Gebiet ist breit gefächert und beschäftigt sich unter anderem mit Themen aus der theoretischen Linguistik (Theorie formaler Sprachen bzw. Automatentheorie), Berechenbarkeits- und Komplexitätstheorie. Ziel dieser Teilgebiete ist es, fundamentale Fragen wie „Was kann berechnet werden?“ und „Wie effizient kann man etwas berechnen?“ umfassend zu beantworten.

• 
  Automatentheorie
• 
  Berechenbarkeitstheorie
• 
  Komplexitätstheorie
• 
  Quantencomputer

Automatentheorie und Formale Sprachen

→ Hauptartikel: Automatentheorie und Formale Sprache

Ein DFA, gegeben als Zustandsübergangsdiagramm

Kellerautomat

1-Band-Turingmaschine

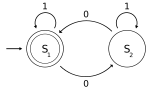
Automaten sind in der Informatik „gedachte Maschinen“, die sich nach bestimmten Regeln verhalten. Ein endlicher Automat hat eine endliche Menge von inneren Zuständen. Er liest ein „Eingabewort“ zeichenweise ein und führt bei jedem Zeichen einen Zustandsübergang durch. Zusätzlich kann er bei jedem Zustandsübergang ein „Ausgabesymbol“ ausgeben. Nach Ende der Eingabe kann der Automat das Eingabewort akzeptieren oder ablehnen.

Der Ansatz der formalen Sprachen hat seinen Ursprung in der Linguistik und eignet sich daher gut zur Beschreibung von Programmiersprachen. Formale Sprachen lassen sich aber auch durch Automatenmodelle beschreiben, da die Menge aller von einem Automaten akzeptierten Wörter als formale Sprache betrachtet werden kann.

Kompliziertere Modelle verfügen über einen Speicher, zum Beispiel Kellerautomaten oder die Turingmaschine, welche gemäß der Church-Turing-These alle durch Menschen berechenbaren Funktionen nachbilden kann.

Berechenbarkeitstheorie

→ Hauptartikel: Berechenbarkeitstheorie

Im Rahmen der Berechenbarkeitstheorie untersucht die theoretische Informatik, welche Probleme mit welchen Maschinen lösbar sind. Ein Rechnermodell oder eine Programmiersprache heißt Turing-vollständig, wenn damit eine universelle Turingmaschine simuliert werden kann. Alle heute eingesetzten Computer und die meisten Programmiersprachen sind Turing-vollständig, das heißt man kann damit dieselben Aufgaben lösen. Auch alternative Berechnungsmodelle wie der Lambda-Kalkül, WHILE-Programme, μ-rekursive Funktionen oder Registermaschinen stellten sich als Turing-vollständig heraus. Aus diesen Erkenntnissen entwickelte sich die Church-Turing-These, die zwar formal nicht beweisbar ist, jedoch allgemein akzeptiert wird.

Den Begriff der Entscheidbarkeit kann man veranschaulichen als die Frage, ob ein bestimmtes Problem algorithmisch lösbar ist. Ein entscheidbares Problem ist zum Beispiel die Eigenschaft eines Texts, ein syntaktisch korrektes Programm zu sein. Ein nicht-entscheidbares Problem ist zum Beispiel die Frage, ob ein gegebenes Programm mit gegebenen Eingabeparametern jemals zu einem Ergebnis kommt, was als Halteproblem bezeichnet wird.

Komplexitätstheorie

→ Hauptartikel: Komplexitätstheorie

Die Komplexitätstheorie befasst sich mit dem Ressourcenbedarf von algorithmisch behandelbaren Problemen auf verschiedenen mathematisch definierten formalen Rechnermodellen sowie der Güte der sie lösenden Algorithmen. Insbesondere werden die Ressourcen „Laufzeit“ und „Speicherplatz“ untersucht und ihr Bedarf wird üblicherweise in der Landau-Notation dargestellt. In erster Linie werden die Laufzeit und der Speicherplatzbedarf in Abhängigkeit von der Länge der Eingabe notiert. Algorithmen, die sich höchstens durch einen konstanten Faktor in ihrer Laufzeit bzw. ihrem Speicherbedarf unterscheiden, werden durch die Landau-Notation derselben Klasse, d. h. einer Menge von Problemen mit äquivalenter vom Algorithmus für die Lösung benötigter Laufzeit, zugeordnet.

Ein Algorithmus, dessen Laufzeit von der Eingabelänge unabhängig ist, arbeitet „in konstanter Zeit“, man schreibt ${\mathcal {O}}(1)$. Beispielsweise wird das Programm „gib das erste Element einer Liste zurück“ in konstanter Zeit arbeiten. Das Programm „prüfe, ob ein bestimmtes Element in einer unsortierten Liste der Länge n enthalten ist“ braucht „lineare Zeit“, also ${\mathcal {O}}(n)$, denn die Eingabeliste muss schlimmstenfalls genau einmal gelesen werden.

Die Komplexitätstheorie liefert bisher fast nur obere Schranken für den Ressourcenbedarf von Problemen, denn Methoden für exakte untere Schranken sind kaum entwickelt und nur von wenigen Problemen bekannt (so zum Beispiel für die Aufgabe, eine Liste von Werten mit Hilfe einer gegebenen Ordnungsrelation durch Vergleiche zu sortieren, die untere Schranke $\Omega (n\log(n))$). Dennoch gibt es Methoden, besonders schwierige Probleme als solche zu klassifizieren, wobei die Theorie der NP-Vollständigkeit eine zentrale Rolle spielt. Demnach ist ein Problem besonders schwierig, wenn man durch dessen Lösung auch automatisch die meisten anderen natürlichen Probleme lösen kann, ohne dafür wesentlich mehr Ressourcen zu verwenden.

Die größte offene Frage in der Komplexitätstheorie ist die Frage nach „P = NP?“. Das Problem ist eines der Millennium-Probleme, die vom Clay Mathematics Institute mit einer Million US-Dollar ausgeschrieben sind. Wenn P nicht gleich NP ist, können NP-vollständige Probleme nicht effizient gelöst werden.

Theorie der Programmiersprachen

Dieser Bereich beschäftigt sich mit der Theorie, Analyse, Charakterisierung und Implementierung von Programmiersprachen und wird sowohl in der praktischen als auch der theoretischen Informatik aktiv erforscht. Das Teilgebiet beeinflusst stark angrenzende Fachbereiche wie Teile der Mathematik und der Linguistik.

• 
  Typentheorie
• 
  Compilerbau
• 
  Programmiersprachen

Theorie der formalen Methoden

Die Theorie der formalen Methoden beschäftigt sich mit einer Vielzahl an Techniken zur formalen Spezifikation und Verifikation von Software- und Hardwaresystemen. Die Motivation für dieses Gebiet entstammt dem ingenieurwissenschaftlichen Denken – eine strenge mathematische Analyse hilft, die Zuverlässigkeit und Robustheit eines Systems zu verbessern. Diese Eigenschaften sind insbesondere bei Systemen, die in sicherheitskritischen Bereichen arbeiten, von großer Bedeutung. Die Erforschung solcher Methoden erfordert unter anderem Kenntnisse aus der mathematischen Logik und der formalen Semantik.

Praktische Informatik

→ Hauptartikel: Praktische Informatik

Die Praktische Informatik entwickelt grundlegende Konzepte und Methoden zur Lösung konkreter Probleme in der realen Welt, beispielsweise der Verwaltung von Daten in Datenstrukturen oder der Entwicklung von Software. Einen wichtigen Stellenwert hat dabei die Entwicklung von Algorithmen. Beispiele dafür sind Sortier- und Suchalgorithmen.

Eines der zentralen Themen der praktischen Informatik ist die Softwaretechnik (auch Softwareengineering genannt). Sie beschäftigt sich mit der systematischen Erstellung von Software. Es werden auch Konzepte und Lösungsvorschläge für große Softwareprojekte entwickelt, die einen wiederholbaren Prozess von der Idee bis zur fertigen Software erlauben sollen.

C-Quelltext		Maschinencode (schematisch)
/** * Berechnung des ggT zweier Zahlen * nach dem Euklidischen Algorithmus */ int ggt(int zahl1, int zahl2) { int temp; while(zahl2 != 0) { temp = zahl1%zahl2; zahl1 = zahl2; zahl2 = temp; } return zahl1; }	→ Compiler →	… 0010 0100 1011 0111 1000 1110 1100 1011 0101 1001 0010 0001 0111 0010 0011 1101 0001 0000 1001 0100 1000 1001 1011 1110 0001 0011 0101 1001 0111 0010 0011 1101 0001 0011 1001 1100 …

Skizze eines B-Baums

Ein wichtiges Thema der Praktischen Informatik ist der Compilerbau, der auch in der Theoretischen Informatik untersucht wird. Ein Compiler ist ein Programm, das andere Programme aus einer Quellsprache (beispielsweise Java oder C++) in eine Zielsprache übersetzt. Ein Compiler ermöglicht es einem Menschen, Software in einer abstrakteren Sprache zu entwickeln als in der von der CPU verwendeten Maschinensprache.

Ein Beispiel für den Einsatz von Datenstrukturen ist der B-Baum, der in Datenbanken und Dateisystemen das schnelle Suchen in großen Datenbeständen erlaubt.

Technische Informatik

→ Hauptartikel: Technische Informatik

Die Technische Informatik befasst sich mit den hardwareseitigen Grundlagen der Informatik, wie etwa Mikroprozessortechnik, Rechnerarchitektur, eingebetteten und Echtzeitsystemen, Rechnernetzen samt der zugehörigen systemnahen Software, sowie den hierfür entwickelten Modellierungs- und Bewertungsmethoden.

Wirkungsspektrum der Technischen Informatik

Mikroprozessortechnik, Rechnerentwurfsprozess

Die Mikroprozessortechnik wird durch die schnelle Entwicklung der Halbleitertechnik dominiert. Die Strukturbreiten im Nanometerbereich ermöglichen die Miniaturisierung von hochkomplexen Schaltkreisen mit mehreren Milliarden Einzelbauelementen. Diese Komplexität ist nur mit ausgereiften Entwurfswerkzeugen und leistungsfähigen Hardwarebeschreibungssprachen zu beherrschen. Der Weg von der Idee zum fertigen Produkt führt über viele Stufen, die weitgehend rechnergestützt sind und ein hohes Maß an Exaktheit und Fehlerfreiheit sichern. Werden wegen hoher Anforderungen an die Leistungsfähigkeit Hardware und Software gemeinsam entworfen, so spricht man auch von Hardware-Software-Codesign.

Architekturen

Die Rechnerarchitektur bzw. Systemarchitektur ist das Fachgebiet, das Konzepte für den Bau von Computern bzw. Systemen erforscht. Bei der Rechnerarchitektur wird z. B. das Zusammenspiel von Prozessoren, Arbeitsspeicher sowie Steuereinheiten (Controller) und Peripherie definiert und verbessert. Das Forschungsgebiet orientiert sich dabei sowohl an den Anforderungen der Software als auch an den Möglichkeiten, die sich über die Weiterentwicklung von Integrierten Schaltkreisen ergeben. Ein Ansatz ist dabei rekonfigurierbare Hardware wie z. B. FPGAs (Field Programmable Gate Arrays), deren Schaltungsstruktur an die jeweiligen Anforderungen angepasst werden kann.

Aufbauend auf der Architektur der sequentiell arbeitenden Von-Neumann-Maschine, bestehen heutige Rechner in der Regel aus einem Prozessor, der selbst wieder mehrere Prozessorkerne, Speicher-Controller und eine ganze Hierarchie von Cache-Speichern enthalten kann, einem als Direktzugriffsspeicher (Random-Access Memory, RAM) ausgelegten Arbeitsspeicher (Primärspeicher) und Ein/Ausgabe-Schnittstellen unter anderem zu Sekundärspeichern (z. B. Festplatte oder SSD-Speicher). Durch die vielen Einsatzgebiete ist heute ein weites Spektrum von Prozessoren im Einsatz, das von einfachen Mikrocontrollern, z. B. in Haushaltsgeräten über besonders energieeffiziente Prozessoren in mobilen Geräten wie Smartphones oder Tabletcomputern bis hin zu intern parallel arbeitenden Hochleistungsprozessoren in Personal Computern und Servern reicht. Parallelrechner gewinnen an Bedeutung, bei denen Rechenoperationen auf mehreren Prozessoren gleichzeitig ausgeführt werden können. Der Fortschritt der Chiptechnik ermöglicht heute schon die Realisierung einer großen Zahl (gegenwärtige Größenordnung 100…1000) von Prozessorkernen auf einem einzigen Chip (Mehrkernprozessoren, Multi/Manycore-Systeme, „System-on-a-Chip“ (SoCs)).

Ist der Rechner in ein technisches System eingebunden und verrichtet dort weitgehend unsichtbar für den Benutzer Aufgaben wie Steuerung, Regelung oder Überwachung, spricht man von einem eingebetteten System. Eingebettete Systeme sind in einer Vielzahl von Geräten des Alltags wie Haushaltsgeräten, Fahrzeugen, Geräten der Unterhaltungselektronik, Mobiltelefonen, aber auch in industriellen Systemen z. B. in der Prozessautomation oder der Medizintechnik im Einsatz. Da eingebettete Computer immerzu und überall verfügbar sind, spricht man auch von allgegenwärtigem oder ubiquitärem Rechnen (Ubiquitous computing). Immer häufiger sind diese Systeme vernetzt, z. B. mit dem Internet („Internet of Things“). Netzwerke von interagierenden Elementen mit physikalischer Eingabe von und Ausgabe zu ihrer Umwelt werden auch als Cyber-Physical Systems bezeichnet. Ein Beispiel sind drahtlose Sensornetze zur Umweltüberwachung.

Heimrouter

Echtzeitsysteme sind darauf ausgelegt, dass sie auf bestimmte zeitkritisch ablaufende Prozesse der Außenwelt mit angemessener Reaktionsgeschwindigkeit rechtzeitig antworten können. Dies setzt voraus, dass die Ausführungszeit der Antwortprozesse entsprechende vorgegebene Zeitschranken garantiert nicht überschreitet. Viele eingebettete Systeme sind auch Echtzeitsysteme.

Eine zentrale Rolle bei allen Mehrrechnersystemen spielt die Rechnerkommunikation. Diese ermöglicht den elektronischen Datenaustausch zwischen Computern und stellt damit die technische Grundlage des Internets dar. Neben der Entwicklung von Routern, Switches oder Firewalls, gehört hierzu auch die Entwicklung der Softwarekomponenten, die zum Betrieb dieser Geräte nötig ist. Dies schließt insbesondere die Definition und Standardisierung von Netzwerkprotokollen, wie TCP, HTTP oder SOAP, ein. Protokolle sind dabei die Sprachen, in denen Rechner untereinander Information austauschen.

Bei Verteilten Systemen arbeitet eine große Zahl von Prozessoren ohne gemeinsamen Speicher zusammen. Üblicherweise regeln Prozesse, die über Nachrichten miteinander kommunizieren, die Zusammenarbeit von einzelnen weitgehend unabhängigen Computern in einem Verbund (Cluster). Schlagworte in diesem Zusammenhang sind beispielsweise Middleware, Grid-Computing und Cloud Computing.

Modellierung und Bewertung

Als Basis für die Bewertung der genannten Architekturansätze sind – wegen der generellen Komplexität solcher Systemlösungen – spezielle Modellierungsmethoden entwickelt worden, um Bewertungen bereits vor der eigentlichen Systemrealisierung durchführen zu können. Besonders wichtig ist dabei zum einen die Modellierung und Bewertung der resultierenden Systemleistung, z. B. anhand von Benchmark-Programmen. Als Methoden zur Leistungsmodellierung sind z. B. Warteschlangenmodelle, Petri-Netze und spezielle verkehrstheoretische Modelle entwickelt worden. Vielfach wird insbesondere bei der Prozessorentwicklung auch Computersimulation eingesetzt.

Neben der Leistung können auch andere Systemeigenschaften auf der Basis der Modellierung studiert werden; z. B. spielt gegenwärtig auch der Energieverbrauch von Rechnerkomponenten eine immer größere, zu berücksichtigende Rolle. Angesichts des Wachstums der Hardware- und Softwarekomplexität sind außerdem Probleme der Zuverlässigkeit, Fehlerdiagnose und Fehlertoleranz, insbesondere bei sicherheitskritischen Anwendungen, von großer Bedeutung. Hier gibt es entsprechende, meist auf Verwendung redundanter Hardware- bzw. Softwareelemente basierende Lösungsmethoden.

Beziehungen zu anderen Informatikgebieten und weiteren Fachdisziplinen

Die Technische Informatik hat enge Beziehungen zu anderen Gebieten der Informatik und den Ingenieurwissenschaften. Sie baut auf der Elektronik und Schaltungstechnik auf, wobei digitale Schaltungen im Vordergrund stehen (Digitaltechnik). Für die höheren Softwareschichten stellt sie die Schnittstellen bereit, auf denen wiederum diese Schichten aufbauen. Insbesondere über eingebettete Systeme und Echtzeitsysteme gibt es enge Beziehungen zu angrenzenden Gebieten der Elektrotechnik und des Maschinenbaus wie Steuerungs-, Regelungs- und Automatisierungstechnik sowie zur Robotik.

Informatik in interdisziplinären Wissenschaften

Unter dem Sammelbegriff der Angewandten Informatik „fasst man das Anwenden von Methoden der Kerninformatik in anderen Wissenschaften … zusammen“. Rund um die Informatik haben sich einige interdisziplinäre Teilgebiete und Forschungsansätze entwickelt, teilweise zu eigenen Wissenschaften. Beispiele:

Computational sciences

Dieses interdisziplinäre Feld beschäftigt sich mit der computergestützten Analyse, Modellierung und Simulation von naturwissenschaftlichen Problemen und Prozessen. Entsprechend den Naturwissenschaften wird hier unterschieden:

• Die Bioinformatik (englisch bioinformatics, auch computational biology) befasst sich mit den informatischen Grundlagen und Anwendungen der Speicherung, Organisation und Analyse biologischer Daten. Die ersten reinen Bioinformatikanwendungen wurden für die DNA-Sequenzanalyse entwickelt. Dabei geht es primär um das schnelle Auffinden von Mustern in langen DNA-Sequenzen und die Lösung des Problems, wie man zwei oder mehr ähnliche Sequenzen so übereinander legt und gegeneinander ausrichtet, dass man eine möglichst optimale Übereinstimmung erzielt (sequence alignment). Mit der Aufklärung und weitreichenden Funktionsanalyse verschiedener vollständiger Genome (z. B. des Fadenwurms Caenorhabditis elegans) verlagert sich der Schwerpunkt bioinformatischer Arbeit auf Fragestellungen der Proteomik, wie z. B. dem Problem der Proteinfaltung und Strukturvorhersage, also der Frage nach der Sekundär- oder Tertiärstruktur bei gegebener Aminosäuresequenz.
  • Die Biodiversitätsinformatik umfasst die Speicherung und Verarbeitung von Informationen zur biologischen Vielfalt. Während die Bioinformatik sich mit Nucleinsäuren und Proteinen beschäftigt, sind die Objekte der Biodiversitätsinformatik Taxa, biologische Sammlungsbelege und Beobachtungsdaten.
  • Künstliches Leben (englisch Artificial life) wurde 1986 als interdisziplinäre Forschungsdisziplin etabliert. Die Simulation natürlicher Lebensformen mit Software- (soft artificial life) und Hardwaremethoden (hard artificial life) ist ein Hauptziel dieser Disziplin. Anwendungen für künstliches Leben gibt es heute unter anderem in der synthetischen Biologie, im Gesundheitssektor und der Medizin, in der Ökologie, bei autonomen Robotern, im Transport- und Verkehrssektor, in der Computergrafik, für virtuelle Gesellschaften und bei Computerspielen.

• Die Chemoinformatik (englisch chemoinformatics, cheminformatics oder chemiinformatics) bezeichnet einen Wissenschaftszweig, der das Gebiet der Chemie mit Methoden der Informatik verbindet und umgekehrt. Sie beschäftigt sich mit der Suche im chemischen Raum, welcher aus virtuellen (in silico) oder realen Molekülen besteht. Die Größe des chemischen Raumes wird auf etwa 10⁶² Moleküle geschätzt und ist weit größer als die Menge der bisher real synthetisierten Moleküle. Somit lassen sich unter Umständen Millionen von Molekülen mit Hilfe solcher Computer-Methoden in silico testen, ohne diese explizit mittels Methoden der Kombinatorischen Chemie oder Synthese im Labor erzeugen zu müssen.

Ingenieurinformatik, Maschinenbauinformatik

Die Ingenieurinformatik, englisch auch als Computational Engineering Science bezeichnet, ist eine interdisziplinäre Lehre an der Schnittstelle zwischen den Ingenieurwissenschaften, der Mathematik und der Informatik an den Fachbereichen Elektrotechnik, Maschinenbau, Verfahrenstechnik, Systemtechnik.
Die Maschinenbauinformatik beinhaltet im Kern die virtuelle Produktentwicklung (Produktionsinformatik) mittels Computervisualistik sowie die Automatisierungstechnik.

Wirtschaftsinformatik, Informationsmanagement

→ Hauptartikel: Wirtschaftsinformatik

Die Wirtschaftsinformatik (englisch (business) information systems, auch management information systems) ist eine „Schnittstellen-Disziplin“ zwischen der Informatik und den Wirtschaftswissenschaften, besonders der Betriebswirtschaftslehre. Sie hat sich durch ihre Schnittstellen zu einer eigenständigen Wissenschaft entwickelt und kann sowohl an Wirtschafts- als auch an Informatik-Fakultäten studiert werden. Ein Schwerpunkt der Wirtschaftsinformatik liegt auf der Abbildung von Geschäftsprozessen und der Buchhaltung in relationalen Datenbanksystemen und Enterprise-Resource-Planning-Systemen. Das Information Engineering der Informationssysteme und das Informationsmanagement spielen im Rahmen der Wirtschaftsinformatik eine gewichtige Rolle. Entwickelt wurde dies an der Fachhochschule Furtwangen bereits 1971. Ab 1974 richteten die damalige TH Darmstadt, die Johannes-Kepler-Universität Linz und die TU Wien einen Studiengang Wirtschaftsinformatik ein.

Sozioinformatik

Die Sozioinformatik befasst sich mit den Auswirkungen von IT-Systemen auf die Gesellschaft, wie sie z. B. Organisationen und Gesellschaft in ihrer Organisation unterstützen, aber auch wie die Gesellschaft auf die Entwicklung von sozial eingebetteten IT-Systemen einwirkt, sei es als Prosumenten auf kollaborativen Plattformen wie der Wikipedia, oder mittels rechtlicher Einschränkungen, um beispielsweise Datensicherheit zu garantieren.

Sozialinformatik

Die Sozialinformatik befasst sich zum einen mit dem IT-Betrieb in sozialen Organisationen, zum anderen mit Technik und Informatik als Instrument der Sozialen Arbeit, wie zum Beispiel beim Ambient Assisted Living.

Medieninformatik

Die Medieninformatik hat die Schnittstelle zwischen Mensch und Maschine als Schwerpunkt und befasst sich mit der Verbindung von Informatik, Psychologie, Arbeitswissenschaft, Medientechnik, Mediengestaltung und Didaktik.

Computerlinguistik

In der Computerlinguistik wird untersucht, wie natürliche Sprache mit dem Computer verarbeitet werden kann. Sie ist ein Teilbereich der Künstlichen Intelligenz, aber auch gleichzeitig Schnittstelle zwischen Angewandter Linguistik und Angewandter Informatik. Verwandt dazu ist auch der Begriff der Kognitionswissenschaft, die einen eigenen interdisziplinären Wissenschaftszweig darstellt, der u. a. Linguistik, Informatik, Philosophie, Psychologie und Neurologie verbindet. Anwendungsgebiete der Computerlinguistik sind die Spracherkennung und -synthese, automatische Übersetzung in andere Sprachen und Informationsextraktion aus Texten.

Umweltinformatik, Geoinformatik

Die Umweltinformatik beschäftigt sich interdisziplinär mit der Analyse und Bewertung von Umweltsachverhalten mit Mitteln der Informatik. Schwerpunkte sind die Verwendung von Simulationsprogrammen, Geographische Informationssysteme (GIS) und Datenbanksysteme.
Die Geoinformatik (englisch geoinformatics) ist die Lehre des Wesens und der Funktion der Geoinformation und ihrer Bereitstellung in Form von Geodaten und mit den darauf aufbauenden Anwendungen auseinander. Sie bildet die wissenschaftliche Grundlage für Geoinformationssysteme (GIS). Allen Anwendungen der Geoinformatik gemeinsam ist der Raumbezug und fallweise dessen Abbildung in kartesische räumliche oder planare Darstellungen im Bezugssystem.

Andere Informatikdisziplinen

Weitere Schnittstellen der Informatik zu anderen Disziplinen gibt es in der Informationswirtschaft, Medizinischen Informatik, Logistikinformatik, Pflegeinformatik und der Rechtsinformatik, Informationsmanagement (Verwaltungsinformatik, Betriebsinformatik), Architekturinformatik (Bauinformatik) sowie der Agrarinformatik, Archäoinformatik, Sportinformatik, sowie neue interdisziplinäre Richtungen wie beispielsweise das Neuromorphic Engineering. Die Zusammenarbeit mit der Mathematik oder der Elektrotechnik wird aufgrund der Verwandtschaft nicht als interdisziplinär bezeichnet. Mit dem Informatikunterricht, besonders an Schulen, befasst sich die Didaktik der Informatik. Die Elementarinformatik beschäftigt sich mit der Vermittlung von grundlegenden Informatikkonzepten im Vorschul- und Grundschulbereich.

Künstliche Intelligenz

→ Hauptartikel: Künstliche Intelligenz

Eine Kohonenkarte beim Lernen

Die Künstliche Intelligenz (KI) ist ein großes Teilgebiet der Informatik mit starken Einflüssen aus Logik, Linguistik, Neurophysiologie und Kognitionspsychologie. Dabei unterscheidet sich die KI in der Methodik zum Teil erheblich von der klassischen Informatik. Statt eine vollständige Lösungsbeschreibung vorzugeben, wird in der Künstlichen Intelligenz die Lösungsfindung dem Computer selbst überlassen. Ihre Verfahren finden Anwendung in Expertensystemen, in der Sensorik und Robotik.

Im Verständnis des Begriffs „Künstliche Intelligenz“ spiegelt sich oft die aus der Aufklärung stammende Vorstellung vom Menschen als Maschine wider, dessen Nachahmung sich die sogenannte „starke KI“ zum Ziel setzt: eine Intelligenz zu erschaffen, die wie der Mensch nachdenken und Probleme lösen kann und die sich durch eine Form von Bewusstsein beziehungsweise Selbstbewusstsein sowie Emotionen auszeichnet.

Die Umsetzung dieses Ansatzes erfolgte durch Expertensysteme, die im Wesentlichen die Erfassung, Verwaltung und Anwendung einer Vielzahl von Regeln zu einem bestimmten Gegenstand (daher „Experten“) leisten.

Im Gegensatz zur starken KI geht es der „schwachen KI“ darum, konkrete Anwendungsprobleme zu meistern. Insbesondere sind dabei solche Anwendungen von Interesse, zu deren Lösung nach allgemeinem Verständnis eine Form von „Intelligenz“ notwendig scheint. Letztlich geht es der schwachen KI somit um die Simulation intelligenten Verhaltens mit Mitteln der Mathematik und der Informatik; es geht ihr nicht um Schaffung von Bewusstsein oder um ein tieferes Verständnis der Intelligenz. Ein Beispiel aus der schwachen KI ist die Fuzzylogik.

Neuronale Netze gehören ebenfalls in diese Kategorie – seit Anfang der 1980er Jahre analysiert man unter diesem Begriff die Informationsarchitektur des (menschlichen oder tierischen) Gehirns. Die Modellierung in Form künstlicher neuronaler Netze illustriert, wie aus einer sehr einfachen Grundstruktur eine komplexe Mustererkennung geleistet werden kann. Gleichzeitig wird deutlich, dass diese Art von Lernen nicht auf der Herleitung von logisch oder sprachlich formulierbaren Regeln beruht – und somit etwa auch die besonderen Fähigkeiten des menschlichen Gehirns innerhalb des Tierreichs nicht auf einen regel- oder sprachbasierten „Intelligenz“-Begriff reduzierbar sind. Die Auswirkungen dieser Einsichten auf die KI-Forschung, aber auch auf Lerntheorie, Didaktik und andere Gebiete werden noch diskutiert.

• 
  Maschinelles Lernen
• 
  Bildverarbeitung
• 
  Mustererkennung
• 
  Kognitionswissenschaft
• 
  Data-Mining

• 
  Evolutionary computation
• 
  Information Retrieval
• 
  Wissensrepräsentation
• 
  Natural language processing
• 
  Robotik

Während die starke KI an ihrer philosophischen Fragestellung bis heute scheiterte, sind auf der Seite der schwachen KI Fortschritte erzielt worden.

Informatik und Gesellschaft

→ Hauptartikel: Informatik und Gesellschaft

„Informatik und Gesellschaft“ (IuG) ist ein Teilbereich der Wissenschaft Informatik und erforscht die Rolle der Informatik auf dem Weg zur Informationsgesellschaft. Die dabei untersuchten Wechselwirkungen der Informatik umfassen die unterschiedlichsten Aspekte. Ausgehend von historischen, sozialen, kulturellen Fragen betrifft dies ökonomische, politische, ökologische, ethische, didaktische und selbstverständlich technische Aspekte. Die entstehende global vernetzte Informationsgesellschaft wird für die Informatik als zentrale Herausforderung gesehen, in der sie als technische Grundlagenwissenschaft eine definierende Rolle spielt und diese reflektieren muss. IuG ist dadurch gekennzeichnet, dass eine interdisziplinäre Herangehensweise, insbesondere mit den Geisteswissenschaften, aber auch z. B. mit den Rechtswissenschaften notwendig ist.

Siehe auch

• Liste bedeutender Personen für die Informatik
• Gesellschaft für Informatik, Österreichische Computer Gesellschaft, Schweizer Informatik Gesellschaft
• Informatikstudium

Literatur

• Theo Bro: Lexikon der Informatik, Datenverarbeitung und Kryptographie – Knoff-Hoff a Niffi, Niffum et Niffo: Mit über 1000 Übungs-Aufgaben für Lernende, Gebundene Ausgabe, Norderstedt 2024, ISBN 978-3-7583-6815-8.
• Herbert Bruderer: Meilensteine der Rechentechnik. Band 1: Mechanische Rechenmaschinen, Rechenschieber, historische Automaten und wissenschaftliche Instrumente, 2., stark erw. Auflage, Walter de Gruyter, Berlin/Boston 2018, ISBN 978-3-11-051827-6.
• A. K. Dewdney: Der Turing Omnibus: Eine Reise durch die Informatik mit 66 Stationen. Übersetzt von P. Dobrowolski. Springer, Berlin 1995, ISBN 3-540-57780-7.
• Les Goldschlager, Andrew Lister: Informatik – Eine moderne Einführung. Carl Hanser, Wien 1986, ISBN 3-446-14549-4.
• Heinz-Peter Gumm, Manfred Sommer: Einführung in die Informatik. 10. Auflage. Oldenbourg, München 2012, ISBN 978-3-486-70641-3.
• Hans Dieter Hellige (Hrsg.): Geschichten der Informatik. Visionen, Paradigmen, Leitmotive. Berlin, Springer 2004, ISBN 3-540-00217-0.
• Jan Leeuwen: Theoretical Computer Science. Springer, Berlin 2000, ISBN 3-540-67823-9.
• Peter Rechenberg, Gustav Pomberger (Hrsg.): Informatik-Handbuch. 3. Auflage. Hanser 2002, ISBN 3-446-21842-4.
• Vladimiro Sassone: Foundations of Software Science and Computation Structures. Springer, Berlin 2005, ISBN 3-540-25388-2.
• Uwe Schneider, Dieter Werner (Hrsg.): Taschenbuch der Informatik. 6. Auflage. Fachbuchverlag, Leipzig 2007, ISBN 978-3-446-40754-1.
• Gesellschaft für Informatik: Was ist Informatik? Positionspapier der Gesellschaft für Informatik. (PDF, ca. 600 kB) Bonn 2005., oder Was ist Informatik? Kurzfassung. (PDF; rund 85 kB).

Weblinks

Wiktionary: Informatik – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Informatik – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Regal:EDV – Lern- und Lehrmaterialien

Wikiversity: Fachbereich Informatik – Kursmaterialien

• Literatur von und über Informatik im Katalog der Deutschen Nationalbibliothek
• Linkkatalog zum Thema Informatik-Fachbereiche an Hochschulen bei curlie.org (ehemals DMOZ)
• Gesellschaft für Informatik (GI)
• Schweizer Informatik Gesellschaft (SI)
• Informatik für Lehrerinnen und Lehrer im ZUM-Wiki
• “Einstieg Informatik” www.einstieg-informatik.de