Gauge-Integral
Das Gauge-Integral (auch: Eichintegral, Henstock-Integral, Henstock-Kurzweil-Integral, Denjoy-Perron-Integral) ist ein Integraltyp deskriptiver Natur, dessen heutige Formulierung erst Mitte des 20. Jahrhunderts von dem Mathematiker Jaroslav Kurzweil (1926–2022)[1] entdeckt wurde. Ralph Henstock widmete sich der Entwicklung der Theorie dieses Integraltyps. Eine zentrale Abschätzung, das sog. Henstock-Lemma, ist nach ihm benannt. Vorläufer ist das (äquivalente) Denjoy-Perron-Integral, das allerdings auf einer sehr technischen und unanschaulichen Definition beruht.
Die Besonderheit des Gauge-Integrals besteht darin, dass jede Ableitungsfunktion automatisch (das heißt ohne Zusatzvoraussetzungen) integrabel ist mit . Daneben treten in der Theorie des Gauge-Integrals bedingt integrable Funktionen auf. Darunter versteht man Funktionen, die zwar integrabel sind, nicht aber deren Betrag. Sowohl bei der Riemann- als auch bei der Lebesgue-Definition folgt aus der Integrierbarkeit einer Funktion stets die Integrierbarkeit ihres Betrags.
Das Gauge-Integral enthält sowohl das Riemann- als auch das Lebesgue-Integral als Spezialfälle, d. h., jede Riemann- bzw. Lebesgue-integrable Funktion ist Gauge-integrabel; da es jedoch Funktionen gibt, die weder Riemann- noch Lebesgue-integrabel, aber dennoch Gauge-integrabel sind, stellt das Gauge-Integral eine echte Erweiterung des Lebesgue-Integrals dar.
Den Namen „Eichintegral“ („gauge“ ist der englische Ausdruck für Eichung) verdankt das Integral seiner Definition: Ähnlich wie das Riemann-Integral kommen auch beim Eichintegral Zerlegungen und Riemann-Summen zum Einsatz, die Feinheit einer Zerlegung wird allerdings mit einer speziellen intervallwertigen Funktion, genannt Eichfunktion, beurteilt.
Einleitung
[Bearbeiten | Quelltext bearbeiten]Der Hauptsatz
[Bearbeiten | Quelltext bearbeiten]Der Hauptsatz der Differenzial- und Integralrechnung (in der gängigen Zählung sein 1. Teil) ist ein zentraler Satz in der Theorie des Riemann- und des Lebesgue-Integrals. Er lautet:
- Satz: Ist eine Ableitungsfunktion von über dem Intervall Riemann- (bzw. Lebesgue-) -integrierbar, so gilt: .
Der Hauptsatz liefert in der Praxis eine der wichtigsten Methoden, den Wert eines Integrals konkret und exakt zu bestimmen. Möchte man etwa die Funktion mit über integrieren, so fasst man f als Ableitungsfunktion einer Funktion , genannt Stammfunktion, auf. Offenbar ist durch eine Stammfunktion von gegeben, sodass folgt:
Sowohl beim Riemann- als auch beim Lebesgue-Integral muss allerdings die Integrierbarkeit von als Voraussetzung angeführt werden – nicht jede Ableitungsfunktion ist unbedingt auch integrabel. Vielmehr zeigt sich, dass es Ableitungsfunktionen gibt, die weder Riemann- noch Lebesgue-integrabel sind. Ein Beispiel ist die Funktion mit

(vgl. Abb. 1). Ihre Ableitung ist durch
gegeben. Da nicht beschränkt ist, ist auch nicht Riemann-integrabel. Man kann zeigen, dass auch nicht Lebesgue-integrierbar ist.
Eine (anschauliche) Analyse der Gründe, aus denen nicht Riemann-integrabel ist, führt zu einer entscheidenden Verbesserung der Riemann-Definition. Dazu überlegt man sich zunächst, woher die Formel überhaupt kommt.
Das Straddle-Lemma und die Probleme des Riemann-Integrals
[Bearbeiten | Quelltext bearbeiten]Nach dem Mittelwertsatz der Differenzialrechnung gibt es zu einer differenzierbaren Funktion auf einem Intervall ein mit
Wählt man zu einer Zerlegung Zwischenstellen nach dem Mittelwertsatz, so erhält man als Ergebnis für Riemannsummen :
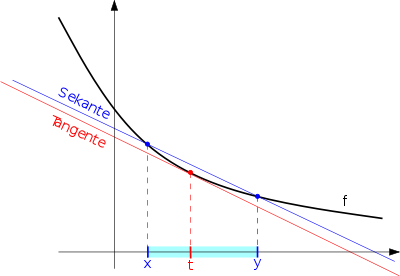
Die letzte Summe stellte dabei eine Teleskopsumme dar. Für andere Zwischenstellen gilt in der obigen Rechnung i. A. keine Gleichheit, doch für den Nachweis von ist es auch nicht erforderlich, dass alle Riemannsummen exakt gleich sind. Es genügt, dass sich die Riemannsummen der Zahl für irgendwelche Zwischenstellen beliebig nähern, sofern man die betrachteten Zerlegungen nur hinreichend fein wählt. Dies wäre etwa dann der Fall, wenn eine Funktion auf jedem Intervall für alle die Näherung
erfüllt, wobei der durch die Näherung entstehende Fehler beliebig klein wird, sofern das Intervall nur hinreichend klein ist (Abb. 2).
Nun gibt es aber Funktionen, die genau dieses Verhalten nicht zeigen. Eine solche Funktion ist die Funktion aus dem vorherigen Abschnitt. Man betrachte etwa das Intervall für irgendein (auch beliebig kleines) : oszilliert nahe 0 „wild hin und her“, daher lässt sich auf jedem Intervall dieser Form (egal, wie klein es auch sei) eine Stelle finden, sodass eine beliebig große positive oder negative Zahl ist. Die durchschnittliche Steigung über dem Intervall hingegen strebt gegen 0, wenn gegen 0 tendiert. Schließlich ist und die durchschnittliche Steigung von g über dem Intervall gerade der Differenzenquotient von an der Stelle 0:
kann also beliebig stark von der durchschnittlichen Steigung auf dem Intervall abweichen. Da jede Zerlegung Z ein Intervall dieser Form „enthält“, gibt es für jede Zerlegung ein Teilintervall und bestimmte Zwischenstellen, für die die Näherung verletzt ist. Dies kann – wie im Fall der Funktion g – dazu führen, dass nicht Riemann-integrabel ist, denn nach der Riemannschen Definition müssen ja alle Zwischenstellen zu einer Zerlegung Z untersucht werden. Wünschenswert wäre eine Integraldefinition, bei der zu bestimmten Teilintervallen auch nur bestimmte Zwischenstellen betrachtet zu werden brauchen. Zwecks Integration der Funktion wäre es z. B. hilfreich, für das Teilintervall nur die Zwischenstelle 0 zuzulassen, denn nach wäre Näherung damit erfüllt.
Eine Integrationstheorie, die auf Riemannsummen basiert und in der jede Ableitungsfunktion integrabel ist, sollte nach den vorherigen Überlegungen nur solche Paare von Zerlegungen und Zwischenstellen berücksichtigen, für die
gilt. Der folgende Satz eröffnet eine Möglichkeit, solche Paare zu identifizieren:
- Satz (Straddle-Lemma): Sei differenzierbar in . Dann gibt es zu jedem ein mit für alle mit und .
Wenn man die Ungleichung des Straddle-Lemmas durch dividiert, wird seine Kernaussage offenbar: Zu jedem Punkt gibt es ein abgeschlossenes Intervall , für das
gilt. Die Zahl gibt den Fehler dieser Näherung an. Da beliebig, also insbesondere beliebig klein sein darf, kann sogar stets ein Intervall gefunden werden, auf dem die obige Näherung beliebig gut ist. Voraussetzung ist lediglich, dass sich die Intervallgrenzen und hinreichend nahe bei befinden, oder anders formuliert: Voraussetzung ist, dass das Intervall in einer hinreichend kleinen Umgebung von liegt:
Wählt man nun nur solche Paare aus der Zerlegung zusammen mit Zwischenstellen aus, für die die Bedingung
zutrifft (wobei nach dem Straddle-Lemma gewählt ist), so ist die Näherung stets erfüllt, und alle zugehörigen Riemann-Summen liegen nahe bei , wie gewünscht.

Es stellt sich nun die Frage, wie man aus allen möglichen Kombinationen von Zwischenstellen und Zerlegungen solche „geeigneten“ Kombinationen auswählt. Der Riemannsche Feinheitsbegriff, d. h. die Betrachtung der größten Intervalllänge , taugt dazu nicht. Offensichtlich gehen die gewählten Zwischenstellen und damit die Positionen der Teilintervalle gar nicht in die Bewertung der Feinheit der Zerlegung ein. Die maßgebliche Zahl aus dem Straddle-Lemma wird jedoch i. A. vom Ort abhängen! Man wird z. B. erwarten, dass umso kleiner ist, desto stärker in der Nähe dieses Punktes oszilliert. Deswegen kann es durchaus passieren, dass für eine Zerlegung und Zwischenstellen die Bedingung erfüllt ist, für eine genauso feine Zerlegung jedoch nicht (vgl. Abbildung 3) – sogar dann nicht, wenn die gleiche Zwischenstelle betrachtet wird. Ziel wird es also sein, einen verbesserten Feinheitsbegriff zu schaffen, der die Position der Teilintervalle berücksichtigt.
Grundideen
[Bearbeiten | Quelltext bearbeiten]Zusammengefasst lauten die „Leitlinien“ für die Definition des Gauge-Integrals:
- Im Rahmen eines neuen Integraltyps sollte jede Ableitungsfunktion automatisch (d. h. ohne Zusatzvoraussetzungen) integrierbar sein mit .
- Dafür muss das Verhältnis zwischen Zwischenstellen und Zerlegungen neu geregelt werden, sodass es möglich wird, Zwischenstellen mit solchen Zerlegungen zu kombinieren, die „gut zusammenpassen“. Dazu muss ein Feinheitsbegriff geschaffen werden, der
- die Positionen der Teilintervalle , , berücksichtigt und
- der es erlaubt, zu bestimmten Teilintervallen auch nur bestimmte Zwischenstellen zuzulassen.
Die formale Definition
[Bearbeiten | Quelltext bearbeiten]Vorarbeiten
[Bearbeiten | Quelltext bearbeiten]Da für das neue Integral nur zueinander „passende“ Zerlegungen und Zwischenstellen betrachtet werden sollen, liegt es nahe, die beiden Begriffe zunächst in einem Begriff zusammenzufügen.
- Definition (markierte Zerlegung). Seien eine Zerlegung eines Intervalls und zu Z gehörige Zwischenstellen, d. h., es gelte für . Die Menge nennt man eine markierte Zerlegung (engl.: tagged partition) des Intervalls .
Eine markierte Zerlegung enthält also geordnete Paare der Form , wobei ein abgeschlossenes Intervall und eine Zahl mit ist. Riemannsummen bzgl. einer Funktion und einer markierten Zerlegung definiert man genau wie Riemannsche Zwischensummen durch:
Die folgende Definition legt den Grund für einen verbesserten Feinheitsbegriff:
- Definition (Eichfunktion): Eine intervallwertige Funktion auf dem Intervall heißt Eichfunktion, wenn und ein offenes Intervall ist.

Eine Eichfunktion ordnet also jedem Punkt ein offenes Intervall zu, das enthält. Über den Begriff der Eichfunktion lässt sich nun ein sehr flexibles Feinheitsmaß definieren, das nicht nur die Position der Teilintervalle einer Zerlegung berücksichtigt, sondern über das sich auch die Beziehung zwischen Zerlegung und Zwischenstellen regeln lässt: Eine markierte Zerlegung soll dann -fein heißen, wenn eine Eichfunktion ist und jedes Teilintervall innerhalb desjenigen offenen Intervalls liegt, das an der zu dem Teilintervall gehörenden Zwischenstelle liefert:
- Definition: Sei eine Eichfunktion auf dem Intervall [a,b] und eine markierte Zerlegung dieses Intervalls. heißt -fein, wenn für alle .
Beispiel
[Bearbeiten | Quelltext bearbeiten]Durch Beschränkung auf -feine Zerlegungen ist es – durch geschickte Wahl der Eichfunktion – möglich, nur passende Paare von Zerlegungen und Stützstellen auszuwählen. Sei etwa und eine Zerlegung dieses Intervalls. Soll (wie im Beispiel der Funktion ) die als einzige mögliche Zwischenstelle zum Teilintervall zugelassen werden, so definiert man wie folgt:
Dabei sei und beliebig. Dann ist das einzige durch gegebene offene Intervall, das die 0 enthält. Für jede markierte Zerlegung von muss aber gelten: . Wegen kann eine markierte Zerlegung nur dann -fein sein, wenn . Das Teilintervall tritt also in jeder -feinen markierten Zerlegung ausschließlich zusammen mit der Zwischenstelle 0 auf. Weiterhin kann aufgrund der -Abhängigkeit der Funktion die Kleinheit eines Teilintervalls einer markierten Zerlegung in Abhängigkeit von der Zwischenstelle und damit von der Position des Teilintervalls „eingestellt“ werden.
Definition des Gauge-Integrals
[Bearbeiten | Quelltext bearbeiten]
Das Gauge-Integral wird nun - ähnlich wie das Riemann-Integral - definiert als eine feste Zahl , der sich Riemannsummen bzgl. markierter Zerlegungen eines Intervalls beliebig nähern, sofern diese Zerlegungen fein bzgl. geeigneter Eichfunktionen gewählt werden:
- Definition (Gauge-Integral): Eine Funktion heißt Gauge-integrabel (eichintegrabel, Henstock- (Kurzweil-) integrabel) über , wenn es zu einer festen Zahl zu jedem eine Eichfunktion auf gibt, sodass für jede -feine markierte Zerlegung gilt. heißt Gauge-Integral (Eichintegral, Henstock- (Kurzweil-) Integral) von über , in Zeichen: .
Die Definition erinnert stark an die (ursprüngliche) Definition des Riemann-Integrals. Der wichtige Unterschied besteht darin, dass das grobe Riemannsche Feinheitsmaß (Betrachtung des längsten Teilintervalls der Zerlegung ) durch das neue, verbesserte Maß ersetzt wurde. Henstock spricht in seinem Werk Theories of Integration daher auch von einem „Integral of Riemann-Type“.
Eigenschaften des Gauge-Integrals
[Bearbeiten | Quelltext bearbeiten]Wie für jeden anderen Integraltyp gilt:
- Der Wert des Gauge-Integrals ist eindeutig bestimmt.
Weiterhin ist die Integralfunktion linear:
- Sind zwei Funktionen über Gauge-integrabel und , dann ist auch Gauge-integrabel über und es gilt: .
Das Riemann-Integral fügt sich zwanglos in den Rahmen des Gauge-Integrals:
- Jede Riemann-integrable Funktion ist auch Gauge-integrabel und die beiden Integrale stimmen überein.
Sei dazu das Riemann-Integral von über und so gewählt, dass für jede Zerlegung mit und beliebige Zwischenstellen . Wählt man die Eichfunktion zu
so gilt für jede -feine markierte Zerlegung per Definition: , also . Definiert man die Zerlegung durch , so ist und somit:
Auch gilt die vom Riemann- und Lebesgue-Integral bekannte Intervalladditivität:
- Seien und zwei nicht überlappende, abgeschlossene Intervalle (d. h., die beiden Intervalle haben höchstens einen Randpunkt gemeinsam) und über Gauge-integrabel. Dann ist auch über Gauge-integrabel und es gilt: .
Umgekehrt findet man:
- Sei über den nicht-überlappenden Intervallen Gauge-integrabel. Ist , so ist auch über integrabel und es gilt:
Das Gauge-Integral ist monoton:
- Ist Gauge-integrabel über und (d. h. ), dann gilt:
- Insbesondere ist , falls .
Besonders interessant ist, dass jede Ableitungsfunktion Gauge-integrabel ist:
- (Hauptsatz, Teil 1). Sei differenzierbar. Dann ist über Gauge-integrabel mit .
Das Ergebnis erhält man nach wenigen geschickten Umformungen, indem man zu die (symmetrische) Eichfunktion wählt, wobei nach dem Straddle-Lemma festgesetzt wird. Dann wertet man für eine beliebige -feine markierte Zerlegung den Ausdruck aus. Der 2. Teil des Hauptsatzes lautet für das Gauge-Integral:
- (Hauptsatz, Teil 2). Sei Gauge-integrabel über . Dann ist die Funktion mit fast überall in [a,b] differenzierbar mit .
Es ist also für das indefinite Integral einer Gauge-integrablen Funktion die Aussage „ ist nicht differenzierbar oder es gilt “ höchstens auf einer Lebesgue-Nullmenge richtig. Wichtig ist, dass nur die Integrierbarkeit von vorausgesetzt werden muss. Ist sogar stetig, so ist überall in differenzierbar mit .
Für das Gauge-Integral gelten die beiden zentralen, vom Lebesgue-Integral bekannten Konvergenztheoreme. Diese beschreiben, unter welchen Umständen die Grenzfunktion einer Funktionenfolge Gauge-integrabler Funktionen wiederum Gauge-integrabel ist und Integration und Grenzwertbildung vertauscht werden dürfen:
Man erhält:

- Satz über monotone Konvergenz: Sei ein Intervall, eine Folge von Funktionen , die über Gauge-integrabel sind und . Konvergiert monoton wachsend gegen , d. h., gilt und für alle , so ist genau dann Gauge-integrabel über , wenn . In diesem Falle gilt:
Konvergiert also eine Funktionenfolge punktweise gegen eine Grenzfunktion und ist die Folge für jedes monoton wachsend und jede Funktion über Gauge-integrabel, so ist die Grenzfunktion dann und nur dann über Gauge-integrabel, wenn die Folge beschränkt ist. In diesem Fall darf die Integration und die Grenzwertbildung vertauscht, dürfen die beiden Operationen also in umgekehrter Reihenfolge ausgeführt werden.
Auch gilt der
- Satz über majorisierte Konvergenz. Sei ein Intervall, eine Folge von Funktionen , die über Gauge-integrabel sind und . Konvergiert punktweise gegen und gibt es Gauge-integrable Funktionen mit fast überall in und alle , so ist über Gauge-integrabel und es gilt:
Gibt es also eine über Gauge-integrable Minorante und eine über Gauge-integrable Majorante für , so ist auch die Grenzfunktion der Funktionenfolge Gauge-integrabel über . Auch in diesem Fall dürfen Grenzwertbildung und Integration vertauscht werden.
Erweiterungen
[Bearbeiten | Quelltext bearbeiten]Im Folgenden ist unter dem Begriff Messbarkeit (und entsprechend verwandten Begriffen) stets Lebesgue-Messbarkeit zu verstehen. Das betrachtete Maß ist also das Lebesgue-Maß auf .
Erweiterungen in einer Dimension
[Bearbeiten | Quelltext bearbeiten]Das Gauge-Integral lässt sich auf unendliche Intervalle ausdehnen. Dies scheint zunächst verwunderlich. Betrachtet man das Intervall als Beispiel, so steht man zunächst vor dem Problem, dass das Intervall nicht abgeschlossen ist. Dieses Problem lässt sich einfach beheben, indem man nicht , sondern die erweiterten reellen Zahlen zugrunde legt. Entsprechend geht man bei der Integration über jedes offene Intervall vor: Man betrachtet dann stets den Abschluss des Intervalls in , also das abgeschlossene Intervall , wobei auch und/oder zugelassen sind. Damit sind aber die Probleme noch lange nicht behoben: Da das Gauge-Integral mit endlichen Zerlegungen arbeitet, ist im Falle eines unendlichen Integrationsbereiches mindestens ein Teilintervall jeder markierten Zerlegung von unendlich lang (entweder oder oder beide) und somit die Summe
bestenfalls unendlich, schlimmstenfalls noch nicht einmal definiert, sofern zwei unendlich lange Intervalle auftreten und f an den jeweiligen Zwischenstellen Werte mit unterschiedlichem Vorzeichen annimmt (dann tritt der undefinierte Ausdruck auf). Man könnte nun ähnlich wie beim Riemann-Integral uneigentliche Integrale definieren, doch es zeigt sich, dass dies durch die Verwendung eines Tricks nicht nötig ist: Dazu untersucht man im Falle eines unendlichen Definitionsintervalls nicht das Integral über , sondern über , gegeben durch:
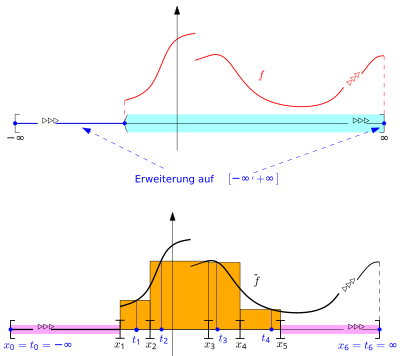
Unten: Die Flächenstücke zwischen und der -Achse über den beiden unendlich langen Intervallen (rot hinterlegt) entfallen, sofern für diese bzw. als Zwischenstellen gewählt werden.
Insbesondere gilt . Innerhalb der Riemannsumme soll dann die Konvention gelten. Demnach ist jede Riemannsumme auch dann definiert, wenn unendlich lange Intervalle enthält, insofern diese nur mit den Zwischenstellen zusammen auftreten. Dies lässt sich aber durch die folgende Definition erzwingen:
- Definition: Das Intervall mit heißt offenes Intervall, das enthält. Analog heißt mit offenes Intervall, das enthält.
Damit ist es nun möglich, Eichfunktionen so zu definieren, dass unendlich lange Teilintervalle ausschließlich zusammen mit als Zwischenstellen auftreten, z. B. für das Intervall :
Dabei können beliebige reelle Zahlen und beliebige positive reelle Funktionen sein. Da und die einzigen Intervalle aus dem Wertebereich von sind, die unendlich lang sind, kann das Teilintervall aus einer -feinen markierten Zerlegung aufgrund der Bedingung nur mit der Zwischenstelle zusammen auftreten. Entsprechendes gilt für das Teilintervall , das nur zusammen mit der Zwischenstelle auftreten kann. Am Beispiel der Zerlegung
und einer Funktion wird klar, warum dadurch das Problem der unendlichen/undefinierten Riemannsummen gelöst ist:
Die beiden potentiell unendlichen Summanden entfallen und die Riemannsumme ist endlich. Mit diesen neuen Definitionen kann das Gauge-Integral problemlos auf unendliche und/oder offene Teilintervalle ausgedehnt werden:
- Definition: Sei irgendein Intervall und sein Abschluss in (d. h., es sind auch und zugelassen). heißt Gauge-integrabel (Henstock- (Kurzweil-) -integrabel, eichintergrabel) über , wenn es zu einer festen Zahl zu jedem eine Eichfunktion auf gibt, sodass für jede -feine markierte Zerlegung Zerlegung von . Man nennt das Gauge-Integral von über , in Zeichen: .
Ist irgendeine messbare Teilmenge eines Intervalls , so nennt man Gauge-integrabel über , falls die Funktion über Gauge-Integrabel ist. Man definiert dann das Gauge-Integral von f über durch:
Ist eine messbare Menge und eine messbare Funktion, so heißt Gauge-integrabel über , wenn die Erweiterung von auf , also die Funktion mit
über Gauge-integrabel ist und man setzt
Es zeigt sich:
- Definiert man uneigentliche Gauge-Integrale ähnlich wie die uneigentlichen Integrale in der Riemann-Theorie, so ist genau dann uneigentlich Gauge-integrierbar über ein unendlich langes Definitionsintervall, wenn es im obigen Sinne eigentlich Gauge-integrabel ist, außerdem stimmen die Werte der Integrale überein.
- Alle im vorherigen Abschnitt genannten Eigenschaften übertragen sich sinngemäß auf das auf unendliche Definitionsintervalle erweiterte Gauge-Integral. Der 1. Teil des Hauptsatzes gilt dann auf jedem endlichen Teilintervall eines unendlich langen Integrationsbereiches , im 2. Teil ist ein beliebiger fester Punkt zu wählen. Der Inhalt des Satzes gilt dann für die Funktion , wobei möglich ist.
Aufgrund der Intervalladditivität fallen alle erweiterten Definitionen mit der ursprünglichen Definition des Gauge-Integrals über Intervalle zusammen, falls ein Intervall ist (jedes Intervall ist messbar). Mit diesen Definitionen gelingt der Anschluss an das Lebesgue-Integral. Es zeigt sich:
- Sei eine messbare Menge. Ist Lebesgue-integrabel über , so ist auch Gauge-integrabel über und die beiden Integrale stimmen überein. Insbesondere gilt: ist genau dann Lebesgue-integrabel über , wenn absolut Gauge-integrabel über ist, d. h. sowohl die Funktion als auch ihr Betrag über Gauge-integrabel sind.
Damit ist das auch Lebesgue-Integral als Spezialfall im Gauge-Integral enthalten.
Das mehrdimensionale Gauge-Integral
[Bearbeiten | Quelltext bearbeiten]Sinngemäß wird das Gauge-Integral auf beliebige Dimensionen fortgesetzt. Wie in einer Dimension definiert man dazu das Integral zunächst über Intervallen. Die Erweiterung auf unendlich große Intervalle soll darin bereits enthalten sein.
- Definition (n-dimensionales Intervall): Eine Menge heißt (n-dimensionales) Intervall, wenn es Intervalle gibt mit .
Ein Intervall in n Dimensionen ist somit als das kartesische Produkt n eindimensionaler Intervalle definiert und besitzt folglich die Gestalt eines n-dimensionalen Quaders. Dabei gilt:
- Definition (offen, abgeschlossen): Ein Intervall heißt offen [abgeschlossen] in , wenn alle offen [abgeschlossen] in sind.
Man beachte, dass auch ein Intervall der Form mit oder als abgeschlossen in bezeichnet wird.

Entsprechend erweitert man die Begriffe der markierten Zerlegung und der Eichfunktion auf Dimensionen:
- Definition (markierte Zerlegung): Sei ein abgeschlossenes Intervall. Eine Menge heißt markierte Zerlegung von , wenn alle Intervalle sind mit und .
Eine markierte Zerlegung eines abgeschlossenen Intervalls ist also eine Menge aus geordneten Paaren , deren erster Eintrag ein Punkt aus , deren zweiter Eintrag dagegen ein Intervall ist. Der zu dem Intervall gehörige Punkt muss dabei in liegen, die Vereinigung aller wiederum das zu zerlegende Intervall ergeben (vgl. Abb. 8).
- Definition (Eichfunktion): Sei ein Intervall. Eine intervallwertige Funktion heißt Eichfunktion auf , wenn ein offenes Intervall und für alle .
Wie im Eindimensionalen soll ein Intervall auch als offen gelten, wenn ein die Gestalt oder mit einer beliebigen reellen Zahl besitzt. Genau wie in einer Dimension definiert man nun mit Hilfe dieser Begriffe die Feinheit einer markierten Zerlegung:
- Definition: Sei eine Eichfunktion auf dem abgeschlossenen Intervall . Eine markierte Zerlegung heißt -fein, wenn für .
Das Volumen eines Intervalls sei gegeben durch
wobei die Länge des (eindimensionalen) Intervalls darstellt. Auch hier soll die Konvention gelten, d. h., besitzt eines der die Länge , so ist , auch wenn ein oder mehrere unendlich lange Intervalle unter den sind.
Jede Funktion wird auf fortgesetzt:
Insbesondere verschwindet in jedem Punkt , der mindestens eine unendliche Komponente aufweist. So ist etwa . Riemannsche Zwischensummen bzgl. einer Funktion und einer markierten Zerlegung werden definiert durch:
Auch hier sei die Konvention gültig. Das Gauge-Integral in Dimensionen kann dann wie folgt festgesetzt werden:
- Definition (n-dimensionales Gauge-Integral): Sei ein Intervall des , dessen Abschluss in . heißt Gauge-integrabel (Henstock- (Kurzweil-) -intergrabel, eichintegrabel) über , wenn es zu einer festen Zahl und zu jedem eine Eichfunktion auf gibt, sodass für jede -feine markierte Zerlegung gilt: . Man schreibt: .
Alle Erweiterungen auf beliebige messbare Teilmengen des geschehen genauso wie beim eindimensionalen Gauge-Integral. Die o. g. Eigenschaften des eindimensionalen Gauge-Integrals übertragen sich sinngemäß auf das mehrdimensionale Gauge-Integral. Weiterhin lassen sich Versionen der Sätze von Fubini und Tonelli für das n-dimensionale Gauge-Integral aufstellen.
Charakterisierung
[Bearbeiten | Quelltext bearbeiten]Das Eichintegral ist deskriptiver Natur, d. h., es beruht auf der Beobachtung, dass Differentiation und Integration üblicherweise vertauschbar sind. Diese Beobachtung in den Vordergrund stellend garantiert das Eichintegral die Vertauschbarkeit im Allgemeinen. Es ergeben sich daher unmittelbar (ohne pathologische Beispiele heranziehen zu müssen) Funktionen, die zwar nicht Riemann-, aber Gauge-integrabel sind, wie z. B. das Reziproke der Wurzelfunktion oder das obige Leitbeispiel.
Literatur und Weblinks
[Bearbeiten | Quelltext bearbeiten]- Ralph Henstock: Theories of Integration. London 1963.
- Douglas S. Kurtz, Charles W. Swartz: Theories of Integration. 2004.
- Internetseite über das Gauge-Integral (englisch)
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Zemřel vědec Jaroslav Kurzweil, významná osobnost české matematiky, tn.nova.cz, 18. März 2022
![{\displaystyle f'\colon {[a,b]}\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/18c5d70eca66486408f80c5f7b16e958ce7c33e5)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle f\colon [0,1]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/58e2f14ce47b691a2fe965e24496bd8931c06a0e)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle F\colon [0,1]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5834f2df268c26cd86dfeb02485aea935ea79dc9)


![{\displaystyle g\colon [0,1]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a73a35d3562faf7c34e57d4abc2b901c308ad741)



![{\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccf6eb823414cc4f75e408522881f3423c52534d)
![{\displaystyle [x,y]\subset [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43eaee652e85b22736388bc38d79b8d83b9b8c83)
![{\displaystyle c\in [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e776ac8bbc711eac38097a3924aa0218f0f706c)


![{\displaystyle c_{i}\in [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0a1f805a20dfe5d6c8ecee409509aa7c980b9dd)



![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)

![{\displaystyle t\in [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4524465ae12079725a45b58ec82830e34b306035)


![{\displaystyle [0,x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ff6e95d26708d1ef54d3bb46e9bfe9bf0cd6a0)










![{\displaystyle t\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f3050ace6dc0dd95250c418528da28eb477ffe)



![{\displaystyle x,y\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e14f38807bc231b9e43d45c8e909d463afb17b5)

![{\displaystyle [x,y]\subset (t-\delta (t),t+\delta (t))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1021717f19ba124fad3a36cc2affd271ed89dd)





![{\displaystyle (3)\ [x_{i-1},x_{i}]\subset (t_{i}-\delta (t_{i}),t_{i}+\delta (t_{i}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd87db82b88a0f38f99411d13a092a7a5b0df375)






![{\displaystyle [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09cb12a889d47020c8ce7046a2eb60785e00c0b6)



![{\displaystyle t_{i}\in [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82811fdf676362991070d2ed9c835e61f95590f6)
![{\displaystyle D=\{(t_{i},[x_{i-1},x_{i}]):i=1,\dots ,n\}=:\{(t_{i},I_{i}):i=1,\dots ,n\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baa2ff2c1d9213b7aeb4c9871c08214a3b6a7e4)









![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

![{\displaystyle D=\{(t_{i},[x_{i-1},x_{i}]):i=1,\dots ,n\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb6981b1f7632762060273035e7e1fdca4caac04)
![{\displaystyle [x_{i-1},x_{i}]\subset \gamma (t_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1264a11163fbca923bc1e8b16f398825bfed3c)
![{\displaystyle I_{i}=[x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a58aa0c124df75a387ac1c5e3edf8289b55c42ac)



![{\displaystyle [a,b]=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9de4d2b73008f49dd28f604a83a1e7423a8f7028)

![{\displaystyle I_{1}=[0,x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e85c7ec76b2bf9404da37ff0e0873da5113529f)









![{\displaystyle f\colon I=[a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a309fdd50f876ee113e6927cca7e41fa096290ea)















![{\displaystyle J_{1},J_{2}\subset [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0e89f2699c11243ea9de8198d8b81ca98364f16)



![{\displaystyle [a,b]=\cup _{j=1}^{m}J_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/703759a91e2a48ff065b9f17aa4caf3e56d664b6)


![{\displaystyle f(x)\geq g(x)\,\forall x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5946ff43886ce5d554236405a359e18bf9489eac)






![{\displaystyle F\colon [a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ce18ea6666c32276447809d9ec4db1f1b29137)

























![{\displaystyle {\overline {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,+\infty \}=[-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1d3b2d3d7d697bab581565d20af3fec8d9d98cb)




![{\displaystyle I=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6214bb3ce7f00e496c0706edd1464ac60b73b5)
![{\displaystyle [x_{0},x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec10faf54bec6a09b997bebef2b4417ec2ebc8b0)
![{\displaystyle [x_{n-1},x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94ddf41cafbd407ce65e95ad57444db64159daa8)


![{\displaystyle {\bar {f}}:[-\infty ,+\infty ]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3dc8c886899fbf5946e06281328a20974f9f28)







![{\displaystyle (a,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9033a825332cf3d1185658136c090d9c24eb837)



![{\displaystyle [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e13233867b861889693a36843d98e51d90d38f9f)
![{\displaystyle \gamma (t)={\begin{cases}[-\infty ,a)&{\text{ für }}t=-\infty \\(t-l(t),t+r(t))&{\text{ für }}t\in \mathbb {R} \\(b,\infty ]&{\text{ für }}t=\infty \end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dbba223f7c67ae20583b433ceffaf09b7eddbf1)




![{\displaystyle [-\infty ,x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186469dcfabf4403622204b8534a63006a7ff481)
![{\displaystyle [-\infty ,x_{1}]\subset \gamma (t_{1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d299a663058dad58501aad72bce08862e8aa8742)

![{\displaystyle [x_{n-1},\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf78892649eeadb75b71deedfd1316a31df39e2f)

![{\displaystyle D=\{(-\infty ,[-\infty ,1]),(1,[0,1]),(2,[1,3]),(\infty ,[3,\infty ])\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88404fc0f23e676e919e2f56b18ec213904c7c6a)

![{\displaystyle S({\bar {f}},D)=\underbrace {{\bar {f}}(-\infty )l([-\infty ,1])} _{=0\cdot \infty =0}+f(1)(2-0)+f(2)(3-1)+\underbrace {{\bar {f}}(\infty )l([3,\infty ])} _{=0\cdot \infty =0}=2f(1)+2f(2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e57e05185f7748a65ed708e09cd9a1284a70bfa9)

![{\displaystyle {\bar {I}}=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe99f89227eeb30337321e0812e95e0bbff7ffa0)

























![{\displaystyle J_{i}=(a,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12670452a662b03b1c72c71bba7300ef39278386)


![{\displaystyle l(J_{i})=l([b_{i},a_{i}])=b_{i}-a_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65b78f90e7a14f8e5750c6065348965fcff7db87)









