Rado-Graph
Der Rado-Graph (auch als Erdős-Rényi-Graph oder Zufallsgraph bezeichnet) ist ein spezieller abzählbar unendlicher Graph, der fast sicher entsteht, wenn jedes Knotenpaar unabhängig und mit Wahrscheinlichkeit durch eine Kante verbunden wird.
Eine wichtige Erkenntnis ist, dass ein Satz in der Prädikatenlogik erster Stufe genau dann für fast alle endlichen Graphen gilt, wenn vom Rado-Graphen erfüllt wird.
Er ist aufgrund von Arbeiten in den 1960er-Jahren nach Richard Rado[1] bzw. Rado, Paul Erdős und Alfréd Rényi[2] benannt, taucht aber schon 1937 bei Wilhelm Ackermann auf.[3]
Definition
[Bearbeiten | Quelltext bearbeiten]
Der Rado-Graph ist definiert als der (ungerichtete) Graph wobei zwei Zahlen mit genau dann durch eine Kante verbunden sind, also gilt, wenn d. h. wenn das -te Bit in der Binärdarstellung von gleich ist. Zum Beispiel hat die Binärdarstellung die an den Stellen und einen Einser hat; also gilt im Rado-Graphen und
Es gibt zahlreiche äquivalente Möglichkeiten, den Rado-Graphen zu definieren, unter anderem durch eine probabilistische Konstruktion: Man nimmt die natürlichen Zahlen als Knotenmenge und verbindet jedes Zahlenpaar mit unabhängig und mit Wahrscheinlichkeit mit einer Kante. Diese Konstruktion liefert fast sicher den Rado-Graphen.[4]
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Erweiterungseigenschaft
[Bearbeiten | Quelltext bearbeiten]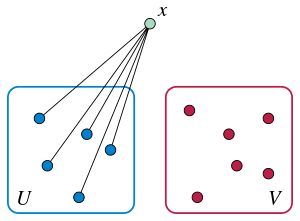
Der Rado-Graph besitzt folgende bemerkenswerte Eigenschaft, die sogenannte Erweiterungseigenschaft: Zu je zwei disjunkten, endlichen Knotenmengen und gibt es stets einen Knoten der zu allen Knoten in und zu keinem Knoten in adjazent ist. Formal erfüllt für alle mit die Formel
Das kann man wie folgt leicht einsehen: Seien und disjunkt, dann sei jene Zahl, die für alle erfüllt und deren andere Bits alle sind. Weil und disjunkt sind, ist wohldefiniert. Nach Konstruktion gilt für alle und für alle
Betrachte hierzu folgendes Beispiel: Sei und dann hat die Binärdarstellung d. h. wobei
Eindeutigkeit
[Bearbeiten | Quelltext bearbeiten]Der Rado-Graph ist bis auf Isomorphie der einzige abzählbare Graph, der die Erweiterungseigenschaft besitzt. Um das zu zeigen, seien und zwei abzählbare Graphen mit Knotenmengen bzw. die die Erweiterungseigenschaft haben. Dann kann man wie folgt einen Isomorphismus mit einer Back-and-forth-Konstruktion bauen: Seien und zwei endliche, zueinander vermöge eines Isomorphismus isomorphe Subgraphen von bzw. und sei jenes Element von mit kleinstem Index, das nicht in vorkommt. Weil die Erweiterungseigenschaft hat, gibt es ein Element , das zu den Elementen von genau dieselben Kanten hat, wie zu den entsprechenden Elementen (bezüglich ) in Ergo kann man zu einem Isomorphismus durch die Vorschrift erweitern, wobei und Anschließend verfährt man völlig analog, um zum Element mit kleinstem Index ein entsprechendes Element zu finden und zu einem Isomorphismus zu erweitern.
Wird abwechselnd jeweils das noch nicht verwendete Element aus bzw. mit kleinstem Index auf diese Art hinzufügt, ist schließlich ein Isomorphismus zwischen und .
Logische Theorie
[Bearbeiten | Quelltext bearbeiten]Offensichtlich folgt die Erweiterungseigenschaft bereits aus der Formelmenge Wie im vorigen Abschnitt gezeigt, ist (zusammen mit der Formel , die besagt, dass die Kantenrelation irreflexiv und symmetrisch ist) ω-kategorisch, d. h. hat bis auf Isomorphie nur ein abzählbares Modell (nämlich den Rado-Graphen). Aus dem Satz von Löwenheim-Skolem folgt daraus unmittelbar, dass eine vollständige Theorie ist. Weil sie des Weiteren axiomatisierbar ist (d. h. rekursiv aufzählbar), ist ihr deduktiver Abschluss aufgrund ihrer Vollständigkeit sogar entscheidbar.
Des Weiteren hat Quantorenelimination.[5]
Null-Eins-Gesetz der Prädikatenlogik erster Stufe
[Bearbeiten | Quelltext bearbeiten]Eng verwandt mit dem Rado-Graphen ist das Null-Eins-Gesetz der Prädikatenlogik erster Stufe:
Für jedes sei die Menge aller nummerierten ungerichteten Graphen mit Knotenmenge Betrachte eine Gleichverteilung auf . Für einen Satz in der Sprache der Graphen sei die Wahrscheinlichkeit, dass in einem zufällig ausgewählten Graphen aus gilt, d. h.
Das Null-Eins-Gesetz besagt nun, dass
Für den Beweis überlegt man sich zuerst Folgendes: Haben zwei Graphen und die Erweiterungseigenschaft , so folgt daraus unmittelbar, dass der Duplikator das -Runden-Ehrenfeucht-Fraïssé-Spiel auf und gewinnt. Nach dem Satz von Ehrenfeucht-Fraïssé bedeutet das, dass in und dieselben Sätze vom Quantorenrang gelten. Nun kann man mit einfachen kombinatorischen Überlegungen und Abschätzungen nachweisen, dass für alle gilt. Also gelten für jedes in fast allen Graphen dieselben Sätze vom Quantorenrang Daraus folgt sofort das Null-Eins-Gesetz, denn jeder Satz hat einen solchen Quantorenrang.
Weil insbesondere der Rado-Graph selbst für jedes die Erweiterungseigenschaft hat, gilt für jeden Satz
Da die Theorie von entscheidbar ist, ist also auch das Berechnungsproblem, welche Sätze in fast allen Graphen gelten, entscheidbar.
Das Null-Eins-Gesetz lässt sich leicht auf beliebige relationale Sprachen verallgemeinern.[6]
Literatur
[Bearbeiten | Quelltext bearbeiten]- Leonid Libkin: Elements of Finite Model Theory, Springer Verlag, 2004, ISBN 9783662070031.
- Wilfrid Hodges: Model Theory (Encyclopedia of Mathematics and its Applications), Cambridge University Press, 1993, ISBN 9780511551574.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Rado, Universal graphs and universal functions, Acta Arithmetica, Band 9, 1964, S. 331–340.
- ↑ Paul Erdős, Alfred Rényi, Asymmetric graphs, Acta Mathematica Academiae Scientiarum Hungaricae, Band 14, 1963, S. 295–315
- ↑ Ackermann, Die Widerspruchsfreiheit der allgemeinen Mengenlehre, Mathematische Annalen, Band 114, 1937, S. 305–315
- ↑ Hodges, S. 351 f.
- ↑ Hodges, S. 350
- ↑ Libkin, S. 240 f.



















































































