Normalenvektor
In der Geometrie ist ein Normalenvektor, auch Normalvektor, ein Vektor, der orthogonal (d. h. rechtwinklig, senkrecht) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Eine Gerade mit diesem Vektor als Richtungsvektor heißt Normale. Ein Normaleneinheitsvektor oder eine Einheitsnormale ist ein Normalenvektor der Länge 1.
In diesem Artikel wird zunächst der Fall von Geraden in der Ebene und von Ebenen im dreidimensionalen Raum behandelt (Lineare Algebra und analytische Geometrie), dann der Fall von Kurven in der Ebene und von Flächen im Raum (Differentialgeometrie).
Lineare Algebra und analytische Geometrie
[Bearbeiten | Quelltext bearbeiten]In diesem Abschnitt werden die Variablen für Vektoren, wie in der Schulmathematik üblich, durch Vektorpfeile gekennzeichnet.
Normale und Normalenvektor einer Geraden
[Bearbeiten | Quelltext bearbeiten]
Ein Normalenvektor einer Geraden in der Ebene ist ein vom Nullvektor verschiedener Vektor, der senkrecht auf dieser Geraden steht, also der Richtungsvektor einer Geraden, die senkrecht auf steht, sprich einer Orthogonalen oder Normalen zu .[1]
Hat den Richtungsvektor , so sind die beiden Vektoren und Normalenvektoren. Durchläuft man die Gerade in der Richtung von , so weist nach links und nach rechts.
Sei eine Gerade in der Ebene und ein Richtungsvektor der Geraden . Der Normalenvektor ist nicht eindeutig und kann mit Mengenschreibweise definiert werden:
Eine sprachliche Formulierung ist dieser Mengenschreibweise ist: Der Normalenvektor ist definiert als die Menge aller Vektoren (ohne den Nullvektor) für die gilt, dass das Skalarprodukt von und einem Richtungsvektor der Geraden gleich Null ist.
Wenn also für einen beliebigen Vektor , gilt, so ist ein Normalenvektor der Geraden .
Ist die Gerade in der Steigungsform durch die Gleichung
gegeben, so ist der Vektor ein Richtungsvektor der Geraden und und sind Normalenvektoren. Für hat also jede Normale die Steigung . Ist , also horizontal, so ist jede Normale vertikal, hat also eine Gleichung der Form .[1]
Ist die Gerade in der allgemeinen Form
gegeben, so ist ein Normalenvektor.[1]
Aus einem Normalenvektor lässt sich ein Normaleneinheitsvektor berechnen, indem durch seine Länge (Norm, Betrag) dividiert wird. Der Vektor wird mithin normiert.
Der zweite Normaleneinheitsvektor ergibt sich durch Multiplikation des obigen Normaleneinheitsvektors mit . Jeder Normalenvektor kann durch Multiplikation eines Normaleneinheitsvektores mit einer reellen Zahl ungleich null gebildet werden.
Normale und Normalenvektor einer Ebene
[Bearbeiten | Quelltext bearbeiten]
Ein Normalenvektor einer Ebene im dreidimensionalen Raum ist ein vom Nullvektor verschiedener Vektor, der senkrecht auf dieser Ebene steht, also der Richtungsvektor einer Geraden, die senkrecht auf steht, sprich einer Orthogonalen oder Normalen zu .[1]
Ist die Ebene in der Koordinatenform durch die Gleichung
gegeben, so ist ein Normalenvektor.[1]
Ist durch zwei aufspannende Vektoren und gegeben (Punkt-Richtungs-Form oder Parameterform), führt die Bedingung, dass der Normalenvektor senkrecht auf und steht, auf ein lineares Gleichungssystem für die Komponenten von :
Jede von verschiedene Lösung liefert einen Normalenvektor.[1]
Eine andere Möglichkeit, Normalenvektoren zu bestimmen, bietet das Kreuzprodukt:[1]
ist ein Vektor, der senkrecht auf und steht, und bilden in dieser Reihenfolge ein Rechtssystem.
Hat die Gleichung
- ,
so ist ein nach oben weisender und ein nach unten weisender Normalenvektor.
Wie im Fall der Gerade in der Ebene erhält man aus einem Normalenvektor einen Normaleneinheitsvektor, indem man ihn durch seine Länge dividiert, einen zweiten durch Multiplikation mit und alle andern Normalenvektoren durch Multiplikation mit reellen Zahlen ungleich 0.
Eine Ebene wird durch einen Normalenvektor sowie einen auf der Ebene liegenden Punkt eindeutig bestimmt, siehe Normalenform und hessesche Normalform.[1]
Normalenvektoren von Kurven und Flächen
[Bearbeiten | Quelltext bearbeiten]Ebene Kurven
[Bearbeiten | Quelltext bearbeiten]
In der Analysis und in der Differentialgeometrie ist der Normalenvektor zu einer ebenen Kurve (in einem bestimmten Punkt) ein Vektor, der auf dem Tangentialvektor in diesem Punkt orthogonal (senkrecht) steht. Die Gerade in Richtung des Normalenvektors durch diesen Punkt heißt Normale, sie ist orthogonal zur Tangente.[1]
Ist die Kurve als Graph einer differenzierbaren Funktion gegeben, so hat die Tangente im Punkt die Steigung , die Steigung der Normalen beträgt also
Die Normale im Punkt ist dann durch die Gleichung
also durch
gegeben.[1]
Ist die ebene Kurve in Parameterform gegeben, , so ist ein Tangentialvektor im Punkt und ein nach rechts weisender Normalenvektor. Hier bezeichnet, wie in der Differentialgeometrie üblich, der Punkt die Ableitung nach dem Kurvenparameter.[1]

Bei Raumkurven bilden die Normalenvektoren in einem Punkt (wie im Fall der Geraden im Raum) einen zweidimensionalen Untervektorraum, der zugehörige affine Unterraum durch , ist die zur Kurve in senkrechte Ebene. In der elementaren Differentialgeometrie wählt man einen Einheitsvektor aus, der in die Richtung zeigt, in die die Kurve gekrümmt ist. Diesen nennt man Hauptnormalen(einheits)vektor, siehe Frenetsche Formeln.
Flächen im dreidimensionalen Raum
[Bearbeiten | Quelltext bearbeiten]
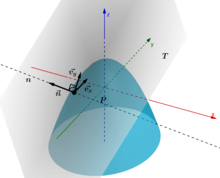
Normale:
Normalenvektor:
Entsprechend ist der Normalenvektor einer gekrümmten Fläche in einem Punkt der Normalenvektor der Tangentialebene in diesem Punkt.
Ist die Fläche durch die Parameterdarstellung
gegeben, so sind die beiden Vektoren
- und
Spannvektoren der Tangentialebene im Punkt . (Hier wird vorausgesetzt, dass die Fläche bei regulär ist, also dass und linear unabhängig sind.) Ein Normalenvektor im Punkt ist ein Vektor, der senkrecht auf und steht, z. B. der durch das Kreuzprodukt gegebene und dann normierte Hauptnormalenvektor
Hier bezeichnen die senkrechten Striche die euklidische Norm des Vektors.[2]
Ist die Fläche implizit durch eine Gleichung gegeben,
- ,
wobei eine differenzierbare Funktion ist, so ist der Gradient
ein Normalenvektor der Fläche im Punkt (vorausgesetzt, dass er dort nicht verschwindet).
Ist die Fläche als Graph einer differenzierbaren Funktion gegeben, so ist
ein nach oben weisender Normalenvektor im Punkt . Dies erhält man, indem man verwendet, dass die Abbildung eine Parametrisierung ist oder dass die Fläche durch die Gleichung
Verallgemeinerungen
[Bearbeiten | Quelltext bearbeiten]Der Begriff des Normalenvektors lässt sich verallgemeinern auf
- affine Unterräume (verallgemeinerte Ebenen) in euklidischen Räumen höherer Dimension (insbesondere auf Hyperebenen),
- Flächen, Hyperflächen und Untermannigfaltigkeiten in euklidischen Räumen höherer Dimension,
- Flächen, Hyperflächen und Untermannigfaltigkeiten von Riemannschen Mannigfaltigkeiten,
- Nichtglatte Objekte, wie konvexe Körper und rektifizierbare Mengen.
Anwendungen
[Bearbeiten | Quelltext bearbeiten]In der Analysis und Differentialgeometrie spielen Normalenvektoren eine zentrale Rolle bei der Berechnung von Oberflächeninhalten und Oberflächenintegralen. Im Bereich der Computergrafik werden Normalenvektoren unter anderem genutzt, um festzustellen, ob eine Fläche dem Benutzer zugewandt ist oder nicht, um letztere von der Bildberechnung auszuschließen (Back-Face Culling). Des Weiteren werden sie zur Berechnung von Lichteinfall und Reflexionen benötigt.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Eric W. Weisstein: normal vector. In: MathWorld (englisch).
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ a b c d e f g h i j k l Normale, Normalenform,Normalenvektor. Ebenengleichung, Geradengleichung In: Schülerduden – Mathematik II. Bibliographisches Institut & F.A. Brockhaus, 2004, ISBN 3-411-04275-3, S. 89–93, 154–156,299–300
- ↑ a b Kurt Endl, Wolfgang Luh: Analysis. Band 2. 7. überarbeitete Auflage. Aula-Verlag, Wiesbaden 1989, ISBN 3-89104-455-0, S. 375–387.









































































