HSV-Farbraum

Der HSV-Farbraum ist der Farbraum etlicher Farbmodelle. Der Farbraum wurde 1978 von A. R. Smith veröffentlicht.[1]
In HSV ist der Farbort einer Farbe definiert mit Hilfe der drei Koordinaten:
- Farbwert (englisch hue): Farbwinkel auf dem Farbkreis (0° für Rot, 120° für Grün, 240° für Blau)
- Farbsättigung (saturation): (0% = Neutralgrau, 50% = wenig gesättigte Farbe, 100% = gesättigte, reine Farbe)
- Hellwert (Helligkeit) (value; auch Dunkelstufe genannt): (0% = keine Helligkeit, 100% = volle Helligkeit)
Ähnliche Definitionen führen zu
- einem HSL-Farbraum mit der relativen Helligkeit (lightness) statt des Hellwertes
- einem HSB-Farbraum mit der absoluten Helligkeit (brightness)
- einem HSI-Farbraum mit der Lichtintensität (intensity).
HSV-Raum und Farbwahrnehmung
[Bearbeiten | Quelltext bearbeiten]
In Fragen der Farbnachstellung wird das HSV-Modell gegenüber den Alternativen RGB und CMYK bevorzugt, weil es der menschlichen Farbwahrnehmung stärker entspricht (beispielsweise ist es im RGB-Modell schwer, sich Gelb als Mischung von Rot und Grün vorzustellen). Für die Farbmischung kann man unmittelbar den gewünschten Farbton wählen und dann entscheiden, wie gesättigt und wie hell (oder dunkel) dieser sein soll, oder ob eine andere Farbnuance passender ist:
- Der Farbwinkel spezifiziert die dominante Wellenlänge der Farbe, mit Ausnahme des Bereiches zwischen Blauviolett und Rot (240° und 360°), wo er eine Position auf der Purpurlinie angibt.
- Die Sättigung entspricht der Zumischung von purem Weiß (d. h. Licht mit gleichen Intensitäten in allen Wellenlängen) zu einer simulierten Spektralfarbe (oder vielmehr der entsprechenden Spaltbreite um die dominante Wellenlänge herum); dabei entspricht stärkere Weiß-Zumischung einer geringeren Sättigung.
- Die Helligkeit ist ein Parameter für den Gesamtenergieinhalt bzw. für die maximale Amplitude des Lichts; die Dunkelstufe ergänzt diesen Wert im Gegensätzlichen. Nachteilig bei der Dunkelstufe ist, dass Weiß und ein beliebiger Farbton die gleiche Sättigung haben können. In diesem System wird Weiß als Buntfarbe behandelt. In der Praxis wiederum ist die Umwandlung eines Farbbildes in ein Schwarz-Weiß-Bild durch Ändern nur einer Koordinate nicht möglich.
RGB und CMYK hingegen sind Wahlmethoden, die an die vorhandenen (geräteabhängigen) Grundfarben gebunden sind, sodass weniger die freie Wahl, sondern das Farbergebnis im Vordergrund steht.
Die HSV-Koordinaten einer Körperfarbe – die notwendigerweise eine Mischfarbe ist – sind nicht unmittelbar aus den Parametern ihres physikalischen Lichtspektrums zu bestimmen, wie dies in der Radiometrie mit den Spektralwertkurven möglich ist. Dagegen wird aus den HSV-Koordinaten mittels geeigneter farbmetrischer Formelsätze auf die Parameter des Spektrums wie Wellenlänge und Amplitude rückgeschlossen. Begrenzend wirkt hier allerdings die Metamerie, da es nicht ohne Probleme möglich ist, aus drei Koordinaten die Vielheit eines Spektrums zu ermitteln; dies ist allerdings kein großes Problem, da das HSV-System meist auch nicht angewendet wird, um die Eigenschaften eines Spektrums zu ermitteln, sondern um Farben auszuwählen.
Visualisierung
[Bearbeiten | Quelltext bearbeiten]Modelle
[Bearbeiten | Quelltext bearbeiten] |
 |
Farbmodelle, die die HSV-Parameter anschaulich darstellen, sind:
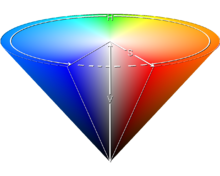
- der auf der Spitze stehende HSV-Kegel, bei dem die Helligkeit von oben (Farbkreis) nach unten (Spitze = Schwarz) abnimmt.
- ein Zylinder, bei dem die Helligkeit zu einer Fläche (anstatt zu einem Punkt) abnimmt.
- eine Halbkugel, das farbmetrisch korrekte Modell.
- eine Pyramide mit sechseckigem Grundriss, die präziser auf das Gamut-Problem eingeht. Allerdings sind die S-Werte nicht direkt ablesbar, oder sie ergeben nur bei den sechs Grundfarben eine Summe von 100%. Die hexagonale Pyramide ist kein Farbraum.
Für die unten beschriebenen HSL-, HSI- und HSB-Modelle ergeben sich Varianten als Doppelkegel, Doppelpyramide oder Kugel.
Aufgrund der vielfältigen Darstellungsformen weichen die HSV-Werte für denselben Farbort teilweise ab, wodurch die Angabe des genutzten Modells unabdingbar wird. Das macht die HSV-Modelle zwar für die Auswahl und Darstellung von Farben hilfreich, in Bezug auf Farbmetrik können jedoch Komplikationen auftreten.
Mit Angabe des verwendeten Modells können HSV-Werte in Lab-Koordinaten umgerechnet werden, die dann auf andere Farbmodelle transferierbar sind.
Farbwähler
[Bearbeiten | Quelltext bearbeiten]
Für Farbwähler in der Informatik ist eine Darstellung des Farbraums durch das HSV-Modell üblich. Um eine bestimmte Farbe mit Hilfe ihrer HSV-Parameter auszuwählen und die Werte zu bestimmen, benutzt man in einem getrennten Diagramm den HSV-Farbkreis, aus dem der Farbton H direkt ausgewählt wird. Danach werden die beiden anderen Parameter S und V gewählt. Dies kann auf einem Dreieck erfolgen, in welchem die Sättigung auf einer Dreiecksseite und auf deren Mittelsenkrechten die Helligkeit abgetragen ist. Eine Variante ist ein im Inneren des Farbkreises liegendes SV-Dreieck, dessen Spitze auf den Farbton im Farbkreis zeigt, die Dreiecksseite der Sättigung endet dabei in dieser Spitze. Darüber hinaus sind auch Varianten mit feststehender senkrechter Achse für S üblich. Ein Programm, das einen solchen Farbwähler verwendet, bestimmt jeweils den zum Farbton H passenden Schnitt durch den Farbkörper und stellt ihn im Dreieck dar. Der Schnitt ist dabei ein senkrecht stehender, radialer Schnitt entlang der Weiß-Schwarz-Achse.
Eine weitere Variante des Farbwählers auf Basis des HSV-Modells stellt eine HV-Ebene dar, neben der ein separater S-Regler zur Verfügung steht. Zur Unterstützung der Farbauswahl durch den Benutzer wird dabei die Sättigung der in der HV-Ebene dargestellten Farbtöne an den jeweiligen Wert des S-Reglers angepasst, sobald dieser verändert wird. Diese Darstellung entspricht einem kegelförmigen bzw. zylindrischen Schnitt durch den Farbraum, wobei die jeweilige Sättigung dem Radius des Schnitts gegenüber der Weiß-Schwarz-Achse entspricht.
Transformation von HSV/HSL und RGB
[Bearbeiten | Quelltext bearbeiten]
| Farbe | H | S | V | H | S | L | R | G | B |
|---|---|---|---|---|---|---|---|---|---|
| Rot | 0° | 100 % | 100 % | 0° | 100 % | 50 % | 100 % | 0 % | 0 % |
| Orangerot | 15° | 100 % | 100 % | 15° | 100 % | 50 % | 100 % | 25 % | 0 % |
| Orange | 30° | 100 % | 100 % | 30° | 100 % | 50 % | 100 % | 50 % | 0 % |
| Orangegelb | 45° | 100 % | 100 % | 45° | 100 % | 50 % | 100 % | 75 % | 0 % |
| Gelb | 60° | 100 % | 100 % | 60° | 100 % | 50 % | 100 % | 100 % | 0 % |
| Grüngelb | 75° | 100 % | 100 % | 75° | 100 % | 50 % | 75 % | 100 % | 0 % |
| Grasgrün | 90° | 100 % | 100 % | 90° | 100 % | 50 % | 50 % | 100 % | 0 % |
| Gelbgrün | 105° | 100 % | 100 % | 105° | 100 % | 50 % | 25 % | 100 % | 0 % |
| Hellgrün | 120° | 100 % | 100 % | 120° | 100 % | 50 % | 0 % | 100 % | 0 % |
| Leichtes Blaugrün | 135° | 100 % | 100 % | 135° | 100 % | 50 % | 0 % | 100 % | 25 % |
| Frühlingsgrün | 150° | 100 % | 100 % | 150° | 100 % | 50 % | 0 % | 100 % | 50 % |
| Grüncyan | 165° | 100 % | 100 % | 165° | 100 % | 50 % | 0 % | 100 % | 75 % |
| Cyan | 180° | 100 % | 100 % | 180° | 100 % | 50 % | 0 % | 100 % | 100 % |
| Blaucyan | 195° | 100 % | 100 % | 195° | 100 % | 50 % | 0 % | 75 % | 100 % |
| Grünblau | 210° | 100 % | 100 % | 210° | 100 % | 50 % | 0 % | 50 % | 100 % |
| Leichtes Grünblau | 225° | 100 % | 100 % | 225° | 100 % | 50 % | 0 % | 25 % | 100 % |
| Blau | 240° | 100 % | 100 % | 240° | 100 % | 50 % | 0 % | 0 % | 100 % |
| Indigo | 255° | 100 % | 100 % | 255° | 100 % | 50 % | 25 % | 0 % | 100 % |
| Violett | 270° | 100 % | 100 % | 270° | 100 % | 50 % | 50 % | 0 % | 100 % |
| Blaumagenta | 285° | 100 % | 100 % | 285° | 100 % | 50 % | 75 % | 0 % | 100 % |
| Magenta | 300° | 100 % | 100 % | 300° | 100 % | 50 % | 100 % | 0 % | 100 % |
| Rotmagenta | 315° | 100 % | 100 % | 315° | 100 % | 50 % | 100 % | 0 % | 75 % |
| Blaurot | 330° | 100 % | 100 % | 330° | 100 % | 50 % | 100 % | 0 % | 50 % |
| Leichtes Blaurot | 345° | 100 % | 100 % | 345° | 100 % | 50 % | 100 % | 0 % | 25 % |
| Kastanie | 0° | 100 % | 50 % | 0° | 100 % | 25 % | 50 % | 0 % | 0 % |
| Oliv | 60° | 100 % | 50 % | 60° | 100 % | 25 % | 50 % | 50 % | 0 % |
| Grün | 120° | 100 % | 50 % | 120° | 100 % | 25 % | 0 % | 50 % | 0 % |
| Blaugrün | 180° | 100 % | 50 % | 180° | 100 % | 25 % | 0 % | 50 % | 50 % |
| Marineblau | 240° | 100 % | 50 % | 240° | 100 % | 25 % | 0 % | 0 % | 50 % |
| Purpur | 300° | 100 % | 50 % | 300° | 100 % | 25 % | 50 % | 0 % | 50 % |
| Weiß | 0° | 0 % | 100 % | 0° | 0 % | 100 % | 100 % | 100 % | 100 % |
| Grau | 0° | 0 % | 50 % | 0° | 0 % | 50 % | 50 % | 50 % | 50 % |
| Schwarz | 0° | 0 % | 0 % | 0° | 0 % | 0 % | 0 % | 0 % | 0 % |
Die Umrechnung folgt dem Formelsatz von Gonzalez und Woods.[2][3]
- (R, G, B): Farbwerte nach RGB. R, G und B liegen dazu im Intervall .
- (H, S, V): Zugehörige HSV-Farbe. H liegt im halboffenen Intervall , um Eindeutigkeit zu gewährleisten, S und V wiederum im Intervall bzw. .
Diese Intervalle gelten für das hier vorgestellte Modell. Andere Formelsätze[4] mit selbem Ergebnis geben Foley und Van Dam[5][6] oder Travis.[7][6]
- Üblich sind auch farbmetrische Angaben von H, S und V, normiert auf , die dadurch denen des RGB-Modells gleichen. Der unten angegebene Formelsatz wäre dann entsprechend einfacher.
- Außerdem sind Werte in Intervallen gebräuchlich (hexadezimal als , oktal als ), die für 8-Bit-Angaben geeignet sind (diskretes Modell). Für die angegebenen Formeln sind solche Werte auf die hier benutzten Intervalle zu normieren. Weiterhin ist zu beachten, ob der Körper für das zugrunde gelegte Modell ein Würfel, eine Kugel, ein Kegel oder ein Doppelkegel ist.
Umrechnung RGB in HSV/HSL
[Bearbeiten | Quelltext bearbeiten]- Vorbedingung:
- Nachbedingung:
Diese Formeln spiegeln einige Eigenheiten der HSV-Werte wider:
- Wenn R = G = B, dann ist H ohne Bedeutung und es wird per Definition H = 0 gesetzt.
- Das ist offensichtlich. Denn wenn S = 0 ist (ungesättigte Farbe), dann liegt der Farbort auf der zentralen Grau-Linie (obige Kegelform), der Farbton ist so ohne Bedeutung und kann nicht sinnvoll angegeben werden.
- Wenn R = G = B = 0, dann ist S ohne Bedeutung und per Definition wird S = 0 gesetzt.
Undefinierte Werte werden aus rechentechnischen Gründen mit „Null“ besetzt.
Umrechnung HSV in RGB
[Bearbeiten | Quelltext bearbeiten]- Vorbedingung:
Es werden das Grundfarbenintervall , der Wert innerhalb dieses Intervalls in und noch drei Hilfswerte bestimmt, die bereits die jeweiligen Streckenlängen enthalten, aber entsprechend auf die Komponenten R, G und B zu verteilen sind:
- Nachbedingung:
Ist S = 0, dann ist die resultierende Farbe Neutralgrau, und die Formel vereinfacht sich zu R = G = B = V.
Abgewandelte Farbmodelle
[Bearbeiten | Quelltext bearbeiten]Teilweise sind andere Zuordnungen des Farbwinkels zum Farbkreis üblich, die sich dann in der Position des Nullpunktes auf der Buntwertskala unterscheiden. Umrechnungen für diese abgewandelten HSV-Räume finden sich bei Gonzalez und Woods[2] [8] oder Foley und Van Dam.[5][9]
HSL
[Bearbeiten | Quelltext bearbeiten] |
Der HSL-Farbraum (auch als HLS bezeichnet) hat die Parameter Farbwinkel H, Farbsättigung S und Farbhelligkeit L. Im Gegensatz zum HSV-Farbraum wird er jedoch auf den zwischen Weiß und Schwarz liegenden Graupunkt als neutrales Grau bezogen. Der Graupunkt liegt in der Mitte und die Buntwerte außen, der Farbkörper wird daher als Doppelkegel, (Doppel-)Zylinder oder sechsseitiges Prisma dargestellt.
Ähnlich aufgebaut ist das CIE-LCh°-Modell mit Farbhelligkeit L, Buntheit C (entspricht der Sättigung) und dem Bunttonwinkel h° (entspricht dem Farbwinkel), das gewissermaßen einem Lab-Farbraum in Zylinderkoordinaten entspricht.
HSB und HSI
[Bearbeiten | Quelltext bearbeiten]An den Bedürfnissen der Farbmetrik und der phototechnischen Reproduktion orientieren sich das HSB- und das HSI-Modell. Auch hierbei steht H für Buntwert (hue) und S für Sättigung. Der Unterschied bezieht sich auf die dritte Koordinate:
- HSB mit der Strahlungsgröße der absoluten Helligkeit B
- HSI mit der Lichtintensität I.
Weblinks
[Bearbeiten | Quelltext bearbeiten]Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Color Gamut Transform Pairs. (pdf) In: alvyray.com. 1978, abgerufen am 1. November 2023 (englisch).
- ↑ a b Rafael Gonzalez, Richard E. Woods: Digital Image Processing. Prentice Hall Press, 2002, ISBN 0-201-18075-8, S. 295.
- ↑ nach HSV color space – Englische Wikipedia, der Formelsatz ist hier etwas anders angegeben
- ↑ Adrian Ford, Alan Roberts: Colour Space Conversions. In: The Colour (color) Equations Document. September 1996, abgerufen am 30. August 2006 (englisch).
- ↑ a b James D. Foley, Andries van Dam, Steven K. Feiner, John F. Hughes: Computer Graphics: Principles and Practice in C. Addison-Wesley, München 1990.
- ↑ a b Adrian Ford, Alan Roberts: HSV: Hue Saturation Value. In: The Colour (color) Equations Document. September 1996, abgerufen am 30. August 2006 (englisch).
- ↑ D. Travis: Effective Color Displays. Theory and Practice. Academic Press, 1991, ISBN 0-12-697690-2.
- ↑ Adrian Ford, Alan Roberts: HSI: Hue Saturation Intensity. In: The Colour (color) Equations Document. September 1996, abgerufen am 30. August 2006 (englisch).
- ↑ Adrian Ford, Alan Roberts: HSL: Hue Saturation Lightness. In: The Colour (color) Equations Document. September 1996, abgerufen am 30. August 2006 (englisch).
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

![{\displaystyle [0,100\,\%]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/447113f999044f6959eb0f4a87ea5c242afcc354)
![{\displaystyle [0,255]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b92f49fdc420e36b9d62c711c3c6ebe7d9fcebc)
![{\displaystyle [0,FF]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a287ab8254e740d4333ae79f41cba354c3eca65)
![{\displaystyle [0,377]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d874bed204c4af0350c4ce433f99664bacd8927)
![{\displaystyle R,G,B\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df509b9bef4211262b8e7f03a4a22614d53245b)







![{\displaystyle H\in [0^{\circ },360^{\circ }],\;S,V,L\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfcb8934fd1bb4219edbe1d3e8df97b03449a880)
![{\displaystyle H\in [0^{\circ },360^{\circ }],\;S,V\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aebd3653a85cc77b76cc23b936a357296572061f)





