Dualismus (Musiktheorie)
Dualismus, auch harmonischer Dualismus, bezeichnet in der Musiktheorie die Ansicht, wonach der Dur- und der Moll-Dreiklang gleichrangige Kategorien sind.[1] Demgegenüber vertreten sog. „monistische“ Theorien eine Vorrangstellung des Durdreiklangs, von dem der Molldreiklang eine Ableitung sei, etwa durch „Trübung“[2] der Terz des Durdreiklangs.
Geprägt wurde der Begriff von Arthur von Oettingen, der „für das Harmoniesystem eine [...] duale, d. h. zweifältig-gegensätzliche Form der Entwickelung, die in einem symmetrischen Bau aller Tongebilde und Klangfolgen sich kund thut“ gegeben sah.[3] Demnach entstammen der Dur- und der Molldreiklang Prozessen, die einander entgegengesetzt sind. Dies begründet ihre Auffassung als Strukturen, die sich symmetrisch zueinander verhalten.[4]
Als wichtige Vertreter dualistischer Theorien gelten neben Oettingen auch Moritz Hauptmann, Hugo Riemann und Sigfrid Karg-Elert. Seit 1950 sind deren Ansätze in der deutschsprachigen Musiktheorie nur noch vereinzelt weiterverfolgt worden, u. a. von Martin Vogel. In der amerikanischen Musiktheorie hingegen gibt es in jüngerer Zeit ein verstärktes Interesse an dieser Tradition.[5]
Oettingen
[Bearbeiten | Quelltext bearbeiten]Nach Hermann von Helmholtz ist der Molldreiklang weniger konsonant als der Durdreiklang.[6] Dem hält Arthur von Oettingen entgegen, dass der Molldreiklang nicht weniger, sondern anders konsoniere. Der Durakkord sei „tonisch consonant“, wobei Oettingen „Tonicität“ eines Intervalls oder eines Akkords als deren Eigenschaft definiert, „als Klangbestandtheil eines Grundtons aufgefasst zu werden“. Der Mollakkord hingegen sei „phonisch consonant“, da sein „phonischer Oberton“ (definiert als tiefster gemeinsamer Oberton der Bestandteile eines Intervalls oder Akkords) mit dem Dreiklang konsoniere. Umgekehrt aber sei der Durdreiklang „phonisch dissonant“, da sein „phonischer Oberton“ dissoniere, während der Molldreiklang „tonisch dissonant“ sei.[7]
Mollakkorde bezeichnet Oettingen nach ihrem „phonischen Oberton“: c–es–g erhält bei ihm das Symbol g°, wobei g „Hauptton“, es „große Terz“ und c „Quinte“ ist. Einen Durakkord wie c–e–g bezeichnet er hingegen als c+:

- Der tonische Grundton von c+ im Beispiel ist C, da die Dreiklangstöne als 4., 5. und 6. Partialton dieses Tons aufgefasst werden.
- Die Töne von g° gelten als die Partialtöne 10, 12 und 15 des tonischen Grundtons As’.
- Der phonische Oberton von c+ ist h’’’’ als 15. Partialton von c’, 12. Partialton von e’ und 10. Partialton von g’.
- Der phonische Oberton von g° ist g’’’ als 6. Partialton von c’, 5. Partialton von es’ und 4. Partialton von g’.
Riemann
[Bearbeiten | Quelltext bearbeiten]Hugo Riemann leitet den Moll-Dreiklang aus einer Untertonreihe ab, die er als Spiegelung der Obertonreihe auffasst:
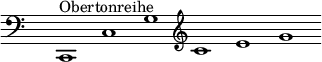
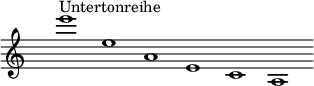
Lange hat Riemann die Überzeugung vertreten, dass eine solche Untertonreihe hörbar sei.[8] Gegen Ende seines Lebens hat er stattdessen eine psychologische Begründung für sie vorgelegt.[9]
Eine Konsequenz davon ist u. a., dass Riemann den Moll-Dreiklang als „Unterklang“ aus einer „Prim“, „Unterterz“ und „Unterquinte“ zusammengesetzt denkt. Den Klang a c e bezeichnet er somit als „e Unterklang“ und übernimmt von Oettingen das Symbol °e (der „c Oberklang“ wird ebenfalls wie bei Oettingen als c+ oder schlicht als c bezeichnet).[10] Die Unterquint eines Unterklangs gilt ihm aber trotzdem als dessen „Grundton“.[11]
Quellen und Literatur (chronologisch)
[Bearbeiten | Quelltext bearbeiten]- Moritz Hauptmann: Die Natur der Harmonik und Metrik. Breitkopf und Härtel, Leipzig 1853 (online).
- Hermann von Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Vieweg, Braunschweig 1863 (online).
- Arthur von Oettingen: Harmoniesystem in dualer Entwicklung. Studien zur Theorie der Musik. Gläser, Dorpat / Leipzig 1866 (online); überarbeitete zweite Auflage als: Das duale Harmoniesystem. Leipzig 1913.
- Hugo Riemann: Musikalische Syntaxis. Grundriß einer harmonischen Satzbildungslehre. Breitkopf und Härtel, Leipzig 1877.
- Hugo Riemann: Vereinfachte Harmonielehre oder die Lehre von den tonalen Funktionen der Akkorde. 1893, 2. Auflage Augener, London 1903 (online).
- Hugo Riemann: Das Problem des harmonischen Dualismus. Leipzig 1905.
- Hugo Riemann: Ideen zu einer ‚Lehre von den Tonvorstellungen‘. In: Jahrbuch der Musikbibliothek Peters 21, 1914, S. 1–26.
- Sigfrid Karg-Elert: Polaristische Klang- und Tonalitätslehre. Leipzig 1930.
- Dale Jorgenson: A Résumé of Harmonic Dualism. In: Music & Letters 44, 1963, S. 31–42.
- Martin Vogel (Hrsg.): Beiträge zur Musiktheorie des 19. Jahrhunderts. Gustav Bosse Verlag, Regensburg 1966.
- Daniel Harrison: Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of Its Precedents. University of Chicago Press 1994, ISBN 9780226318097.
- Henry Klumpenhouwer: Dualist tonal space and transformation in nineteenth-century musical thought. In: Thomas Christensen (Hrsg.): The Cambridge History of Western Music Theory. Cambridge University Press, Cambridge 2002, ISBN 978-0-521-62371-1, S. 456–476.
- Alexander Rehding: Hugo Riemann and the birth of modern musical thought. Cambridge University Press, Cambridge 2003, ISBN 978-0-521-09636-2.
- Edward Gollin: Neo-Riemannian Theory. In: Zeitschrift der Gesellschaft für Musiktheorie 2/2-3 (2005), S. 153–155 (online).
- Andreas Jakubczik: Der „harmonische Dualismus“ von Arthur von Oettingen bis Martin Vogel. GRIN, München 2005, ISBN 978-3-638-33969-8.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Klumpenhouwer 2002, S. 459.
- ↑ Helmholtz 1863, S. 451f.
- ↑ Oettingen 1866, IV.
- ↑ Siehe auch Jorgenson 1963, S. 31: "Harmonic dualism has been defined as a means of explaining the minor triad in a reverse sense from the explanation of the major triad."
- ↑ Siehe z. B. Harrison 1994 und Gollin 2005.
- ↑ Helmholtz 1863, S. 451f.
- ↑ Oettingen 1866, S. 32–33, 45.
- ↑ Riemann 1877, S. 121. Siehe dazu u. a. Rehding 2003, S. 16.
- ↑ Riemann 1914.
- ↑ Riemann 1903, S. 11.
- ↑ Riemann 1903, S. 14. Siehe auch Elmar Seidel: Die Harmonielehre Hugo Riemanns. In: Vogel (Hrsg.) 1966, S. 45: „Bezeichnenderweise nennt Riemann den Bezugston („Hauptton“) des Moll-akkordes nie Grundton.“