Hodograph
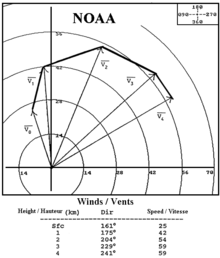
Der Hodograph (v. gr. hodós „Weg“) der Bewegung eines Teilchens ist die Abbildung des Geschwindigkeitsvektors als Funktion der Zeit, oder genauer: die Menge der Endpunkte der von einem festen Punkt aus abgetragenen Geschwindigkeitsvektoren.
Er wurde wahrscheinlich erstmals von James Bradley benutzt, doch seine praktische Entwicklung und Verbreitung ist hauptsächlich William Rowan Hamilton zuzuschreiben, der einen Bericht darüber 1846 in der Proceedings of the Royal Irish Academy veröffentlichte.
Die Definition des Hodographs besagt, dass der Abstand der Kurve vom Ursprung immer dem Betrag der Geschwindigkeit entspricht und die Verbindungslinie vom Ursprung zum Punkt auf der Kurve die Richtung der Geschwindigkeit des Teilchens angibt. Daraus folgt, dass die Tangente an die Hodograph-Kurve zu jeder Zeit die Richtung der Beschleunigung des Teilchens anzeigt.
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- David L. Goodstein, Judith R. Goodstein: Feynmans verschollene Vorlesung: Die Bewegung der Planeten um die Sonne, Piper Verlag GmbH, München 1998, ISBN 3-492-22994-8 – In diesem Buch wird der Hodograph benutzt, um die elliptischen (keplerschen) Orbits geometrisch aus den Newtonschen Bewegungs- und Gravitationsgesetzen abzuleiten.
- William R. Hamilton: The hodograph or a new method of expressing in symbolic language the Newtonian law of attraction Proc. Roy Irish Acad 3, 344–353, 1846.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Hodograph. In: Lexikon der Physik. Spektrum Akademischer Verlag, Heidelberg 1998 (spektrum.de [abgerufen am 23. Januar 2018]).
- J. B. Calvert: The Hodograph. 10. März 2003, abgerufen am 23. Januar 2018 (englisch).