Hohlleiter

Ein Hohlleiter ist ein Wellenleiter für elektromagnetische Wellen vorwiegend im Frequenzbereich von 1 bis 1500 GHz.^[1] Hohlleiter sind Metallrohre mit meist rechteckigem, kreisförmigem oder elliptischem Querschnitt. Mit ihnen lässt sich elektrische Leistung im genannten Frequenzbereich viel verlustärmer als mit elektrischen Kabeln wie Koaxialkabeln übertragen. Aufgrund der Bauweise sind Hohlleiter bevorzugt im Einsatz für hohe Leistungen oder sehr hohe Frequenzen, da auf einen leitenden Mittelleiter wie bei einem Koaxialkabel verzichtet werden kann. Da ein Hohlleiter in der Praxis allein aus Metall bestehen muss, ist dieser auch besonders robust gegenüber Umwelteinflüssen wie extreme Temperaturen, Vibrationen oder Kosmische Strahlung und findet daher häufig Anwendung in der Luft- und Raumfahrt, sowie in Sendeanlagen an Land und auf Schiffen.

Physikalischer Hintergrund

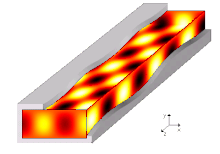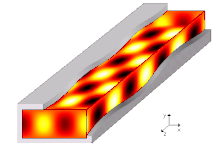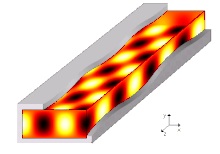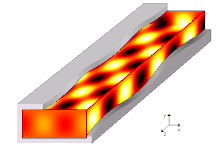
Trifft eine elektromagnetische Welle senkrecht auf eine elektrisch leitende Grenzfläche, wird sie in sich selbst reflektiert. Bei geeignetem Abstand einer parallelen zweiten Grenzfläche bildet sich eine Stehende Welle. Kommen seitliche Wände hinzu, entsteht ein Hohlraumresonator. Auch in diesem sind die elektromagnetischen Wellen stehende Wellen; es handelt sich um ein ortsfestes elektrisches und magnetisches Wechselfeld. Die möglichen Resonanzfrequenzen der stehenden Wellen hängen vom Abstand der Wände zueinander ab.

In einem Hohlleiter bewegt sich dagegen das elektrische und magnetische Wechselfeld fort:

Man stelle sich ein langes Rohr mit rechteckigem Querschnitt vor, in dem eine ebene Welle senkrecht auf eine Schmalseite trifft und zwischen beiden Wänden hin und her reflektiert wird. Die Wellenlänge ist doppelt so groß wie der Abstand der beiden Wände, sodass eine stehende Welle entsteht. Wird nun der Abstand zwischen den beiden Wänden etwas verkleinert, so kann sich die Welle nur in einem speziellen Winkel ausbreiten, bei dem zwischen den beiden Wänden wieder eine stehende Welle entsteht. Dazu muss die Wellenlänge entlang der längeren Wand wieder doppelt so groß wie der Abstand der beiden Wände sein. Die resultierende Wellenlänge in Längsrichtung führt zu einer Wellenausbreitung entlang des Hohlleiters. Man spricht daher zur Unterscheidung von stehenden Wellen auch von einer Wanderwelle.

Die Mindestbreite eines Rechteckhohlleiters entspricht etwa der halben Wellenlänge der übertragenen Frequenz – genau dann passt nur ein einziger Schwingungsbauch in Querrichtung hinein. Man kann daher aus der Breite eines Rechteck-Hohlleiters auf die im zugehörigen Gerät verwendete niedrigste Frequenz schließen. Die dazugehörige Wellenlänge nennt man die kritische Wellenlänge λ_k oder die Grenzwellenlänge λ_c (mit c für „cut-off“). Sie errechnet sich nach der Beziehung λ_k = 2 · a (wobei a die längere Seite des Rechteckhohlleiterquerschnitts ist, siehe Skizze oben). Durch die Erweiterung zum Hohlleiterfilter können gezielt bestimmte Frequenzbereiche unterdrückt werden.

Hohlleiter können auch mit erhöhtem Gas-Innendruck betrieben werden, um (dem Paschen-Gesetz entsprechend) höhere Leistungen übertragen zu können, ohne dass Überschläge beziehungsweise Luftdurchschläge auftreten. Das Phänomen Multipaction bedeutet in diesem Zusammenhang die konstruktive Überlagerung mehrerer verschiedener Wellenlängen, wodurch sehr hohe Feldstärken entstehen können.

Moden

Die beschriebene Art der Ausbreitung kann so erfolgen, dass ein ganzzahliges Vielfaches der halben Wellenlänge zwischen die Schmalseiten passt. Die verschiedenen möglichen Zustände sind die sogenannten Schwingungsmoden, kurz Moden, und werden mit den Zahlen bezeichnet, die diesem Vielfachen entsprechen; also: 1, 2, 3, …

Bei höheren Frequenzen gesellen sich zu den horizontalen transversalen Moden noch die vertikalen zwischen Ober- und Unterseite des Rohrs, wo unabhängig wiederum verschiedene Moden auftreten. Deshalb ist zur Beschreibung einer Mode im rechteckigen Hohlleiter jeweils die Angabe zweier Zahlen notwendig, der Modenordnung: z. B. (2,3)-Mode. Dabei steht je eine der Zahlen für eine der transversalen Moden in Richtung der elektrischen und der magnetischen Feldkomponente (E- und H-Richtung).

Die Feldlinien des elektrischen Feldes stehen immer senkrecht auf dem Außenleiter und verlaufen von einer Wandseite zur anderen. Je nachdem, wie viele Extremwerte der Feldverlauf über die gesamte Breite des Hohlleiters aufweist, erhält die Modenbezeichnung ihren ersten Index. Die Breite eines Hohlleiters wird mit a bezeichnet. Bei einem Maximum, der Mindestanzahl für die elektrische Feldverteilung, spricht man also von einer $H_{1m}$ - bzw. $E_{1m}$ Welle.

Analog bezeichnet die Anzahl an Maxima im Feldverlauf des elektrischen Felds über die gesamte Höhe des Hohlleiters den zweiten Index. Die Höhe eines Hohlleiters wird mit b bezeichnet. Die Feldstärke kann über die gesamte Hohlleiterhöhe konstant bleiben (es muss also kein Maximum geben), man spricht dann von einer $H_{n0}$ bzw. $E_{n0}$ Welle.

Vergleichbare Moden gibt es auch in runden Hohlleitern. Hier kommen jedoch noch Moden hinzu, die entlang des Rohrumfanges eine homogene Feldverteilung haben.

Die Ein- und Auskopplung der HF-Energie erfolgt durch Schlitze, Koppelschleifen, Stäbe, Trichter (Hornstrahler) oder Löcher – je nachdem, ob die Energie in einen anderen Hohlleiter, in ein Koaxialkabel oder ins Freie gelangen soll. Ort und Gestalt dieser Koppelelemente bestimmen die Mode und die Ausbreitungsrichtung der Wellen.

E-/H-Moden

Elektrisches und magnetisches Feld stehen bei elektromagnetischen Wellen immer senkrecht aufeinander. Damit die Welle sich in einer Raumrichtung fortpflanzen kann, müssen Wellenkomponenten in diese Raumrichtung existieren. Steht das elektrische Feld senkrecht zur Ausbreitungsrichtung z, spricht man von H-Moden. Steht das magnetische Feld senkrecht zur Ausbreitungsrichtung, spricht man von E-Moden. Die Abbildung zeigt einen Längsschnitt durch einen Hohlleiter (z-Richtung).

Hohlleiterwellenlänge und Grenzfrequenz

Während der Abstand der Maxima der Feldverteilung in x- bzw. y-Richtung von der Freiraumwellenlänge der Welle abhängt, ist für den Abstand der Maxima in z-Richtung, also in Ausbreitungsrichtung, die Hohlleiterwellenlänge entscheidend.

Die Hohlleiterwellenlänge $\lambda _{H,nm}$ hängt gemäß obiger Gleichung von der Modenordnung, der Freiraumwellenlänge $\lambda _{0}$ sowie von Breite $a$ und Höhe $b$ des Hohlleiters ab, nicht jedoch davon, ob die Mode elektrisch oder magnetisch ist. Sie ist immer größer als die Freiraumwellenlänge gleicher Frequenz und die Phasengeschwindigkeit in z-Richtung entsprechend größer als die Lichtgeschwindigkeit.

Der Zusammenhang ist nicht-linear, und es existiert für gegebene Modenordnung und Abmessungen eine Freiraumwellenlänge, für die die Hohlleiterwellenlänge gegen unendlich geht:

\lambda _{H,nm}={\frac {\lambda _{0}}{\sqrt {1-\lambda _{0}^{2}\left[\left({\frac {n}{2a}}\right)^{2}+\left({\frac {m}{2b}}\right)^{2}\right]}}}

Eine divergierende Hohlleiterwellenlänge bedeutet, dass die Welle nicht ausbreitungsfähig ist (Gruppengeschwindigkeit null). Da die Hohlleiterwellenlänge für einen Mode einer bestimmten Frequenz von den Abmessungen des Hohlleiters abhängt, sind in einem Hohlleiter nicht beliebige Moden ausbreitungsfähig. Je höherwertig ein Mode ist, desto größer ist seine Grenzfrequenz, bzw. desto kleiner ist die Grenzwellenlänge $\lambda _{\mathrm {grenz,} nm}$ .

\lambda _{\mathrm {grenz,} nm}={\frac {1}{\sqrt {\left({\frac {n}{2a}}\right)^{2}+\left({\frac {m}{2b}}\right)^{2}}}}={\frac {c}{f_{\mathrm {grenz} }}}

Die Grenzfrequenz teilt den Frequenzbereich in zwei Bereiche, den Dämpfungsbereich und den Ausbreitungsbereich. Entscheidend ist hierbei das Verhalten des Ausbreitungskoeffizienten γ über der Frequenz.

Im Dämpfungsbereich ist die Welle nicht ausbreitungsfähig. Der Ausbreitungskoeffizient ist als $\alpha _{\mathrm {max} }$ rein reell. Die Welle wird demnach aperiodisch gedämpft. Nicht ausbreitungsfähige Moden können angeregt werden und zumindest zeitweilig einen Teil der Wellenenergie binden. Ist die Frequenz der Welle gleich der Grenzfrequenz, so ist der Ausbreitungskoeffizient gleich Null. Die Welle wird im rechten Winkel zwischen den Seiten des Hohlleiters reflektiert, ohne dass ein Energietransport stattfindet.

Für Frequenzen oberhalb der Grenzfrequenz ist die Welle ausbreitungsfähig. Der Ausbreitungskoeffizient ist im Idealfall $\beta _{\infty }$ und damit rein imaginär. Die Welle wird demnach nicht gedämpft, sondern breitet sich im Hohlleiter mit einer frequenzabhängigen Phasenverschiebung aus. Im realen Hohlleiter wird auch eine ausbreitungsfähige Welle gedämpft. Dazu tragen die Verluste in der nur endlich leitfähigen Hohlleiterwand (Oberflächenströme) bei. Der (Verlust)anteil der Oberflächenströme am Leistungstransport ist modenabhängig, sinkt tendenziell mit höheren Moden und steigt tendenziell aufgrund des Skineffektes. Da Hohlleiter in der Regel luft- oder gasgefüllt sind, treten keine dielektrischen Verluste auf. Das ist ein wesentlicher Faktor für ihren Einsatz bei sehr hohen Frequenzen.

Wellenimpedanz

Die Wellenimpedanz verknüpft die Amplituden der elektrischen und magnetischen Feldstärken einer elektromagnetischen Welle. Im Hohlleiter ist sie frequenzabhängig und unterscheidet sich für TM- und TE-Modus, besitzt aber überall im Hohlleiter den gleichen Wert.

Z={\frac {Z_{w0}}{\sqrt {1-\left({\frac {f_{\text{grenz}}}{f}}\right)^{\!2}}}}\qquad {\text{(TE-Mode)}},

wobei f_grenz die cut-off Frequenz des jeweiligen Modes bedeutet und $Z_{w0}\approx 376{,}73\,\Omega$ der Freiraumwellenwiderstand ist.

Z=Z_{w0}\ {\sqrt {1-\left({\frac {f_{\text{grenz}}}{f}}\right)^{\!2}}}\qquad {\text{(TM-Mode)}}

Oberhalb der Grenzfrequenz (f > f_grenz) ist die Impedanz reellwertig und im Hohlleiter pflanzt sich Energie fort. Unterhalb der Grenzfrequenz ist die Impedanz dagegen imaginär und die Welle wird im Hohlleiter gedämpft und verliert schnell an Amplitude.

Verschiedene Hohlleiter und ihre Moden

Viele charakteristische Eigenschaften sind allen Hohlleitertypen gemeinsam. Dazu gehört eine cut-off-Frequenz, unterhalb der keine Wellenausbreitung stattfindet.

Während sich in einem Koaxialkabel TEM-Wellen ausbreiten (elektrische und magnetische Felder sind stets senkrecht zur Ausbreitungsrichtung), finden sich in einem Hohlleiter ausschließlich sogenannte H-Wellen (auch TE-Wellen) und E-Wellen (TM-Wellen), bei denen die magnetischen beziehungsweise die elektrischen Feldkomponenten in Ausbreitungsrichtung weisen.

Hohlleiter weisen ein Hochpassverhalten auf, mit $f_{c}=c/\lambda _{c}$ als Grenzfrequenz. Rechteck- wie Rundhohlleiter zeigen die unten genannten Grundwellentypen. Haben diese Grundwellen (bezogen auf H- bzw. E-Wellen) aufgrund der Abmessungen der Hohlleiter keine Möglichkeit, sich auszubreiten, werden sich auch keine anderen Wellentypen ausbreiten. Siehe auch Hohlraumresonator. Oberhalb der Grenzfrequenz hängt die Ausbreitung der Wellen (beispielsweise Gruppengeschwindigkeit, Phasengeschwindigkeit und Wellenlänge) von der Frequenz ab. Die Wellenausbreitung im Hohlleiter ist somit prinzipiell dispersiv.

Folgende Regeln gelten für die Existenz von Moden:

Elektrische und magnetische Feldlinien stehen stets senkrecht aufeinander.
Magnetische Feldlinien sind immer geschlossen und können nicht auf Wände treffen – sie können Wände nur tangieren.
Elektrische Feldlinien können nicht entlang den Wänden auftreten, sondern nur senkrecht auf sie treffen.

Rechteckhohlleiter

Für einen Rechteckhohlleiter ist, wie vorangehend bereits erwähnt, die größte Abmessung ausschlaggebend. Das heißt, die Breite bestimmt die ausbreitungsfähigen Wellen in diesem Leiter.

Für die E-Welle in Ausbreitungsrichtung gilt:

E_{z}=E_{0}\cdot \sin \left({\frac {m\cdot \pi \cdot x}{a}}\right)\cdot \sin \left({\frac {n\cdot \pi \cdot y}{b}}\right)\cdot \mathrm {e} ^{\;\!\mathrm {j} (\omega t-\beta z)}\,

wobei m und n die Modenzahlen darstellen (m: x-Richtung (quer) und n: y-Richtung (vertikal) bzgl. Ausbreitung in Längsrichtung z). a ist die größere Abmessung des Hohlleiters. Siehe auch Maxwellsche Gleichungen.

Hieraus ergibt sich, dass der Grundwellentyp der E-Wellen die $E_{11}$ -Welle ist, da obige Gleichung mit den Werten m = 0 oder n = 0 zu $E_{z}=0$ führt und somit keine E-Komponente in Ausbreitungsrichtung besteht. Somit müssen im Rechteckhohlleiter mindestens $E_{11}$ -Wellen in Ausbreitungsrichtung entstehen können.

Typisch für Rechteckhohlleiter ist jedoch die $H_{\;\!\!10}$ -Welle.

Rundhohlleiter

Für den Rundhohlleiter ergeben sich die Schwingungsmoden über die Besselfunktion und deren Ableitungen sowie Nullstellen, mit welchen die ausbreitungsfähigen H- und E-Wellen für den Rundhohlleiter bestimmt werden können. Für den Rundhohlleiter erhält man mit dem Radius $R$ als Grundmode $H_{11}$ ; deren Grenzwellenlänge $\lambda _{c}$ berechnet sich über die erste Nullstelle der ersten Ableitung der Besselfunktion erster Ordnung, die an der Stelle 1,841 liegt:

\lambda _{c}={\frac {2\pi R}{1{,}841}}\,.

Die Dämpfung der $H_{11}$ -Welle ist höher als die der $H_{01}$ -Welle. Deshalb ist es oft wünschenswert, die Ausbreitung der $H_{11}$ -Welle zu verringern. Dazu wird die Innenseite eines Rundhohlleiters mit Rillen versehen. Diese stören nur die Ausbreitung der $H_{11}$ -Welle (siehe Bild unten, Hohlleiter mit elliptischem Querschnitt). Die Grenzwellenlänge der $H_{01}$ -Welle berechnet sich mit:

\lambda _{c}={\frac {2\pi R}{3{,}832}}\,.

Somit ist die Grenzwellenlänge der $H_{01}$ kleiner als die der Grundwelle $H_{11}$ , weswegen sich der Hohlleiter für die $H_{01}$ -Welle nicht mehr monomodig verhält.

Hohlleiter mit elliptischem Querschnitt

Neben Rechteck- und Rundhohlleitern finden auch Hohlleiter mit elliptischem Querschnitt Verwendung. Die Grenzwellenlänge entspricht auch bei ihnen grob der doppelten Querabmessung (λ_k ≈ 2·a). Als Faustregel gilt, dass elliptische Hohlleiter in ihren Querabmessungen etwas größer sind als ein Rechteckhohlleiter mit gleicher Grenzfrequenz.

Elliptische Hohlleiter lassen sich technisch günstig auch als flexible Leitungen gestalten. So können größere Längen davon in Rollen oder auf „Kabel“-trommeln aufbewahrt und transportiert werden. Auch lassen elliptische Hohlleiter kleinere Biegeradien zu als runde oder eckige.

Anschlüsse und Verbindungen eines Hohlleiters

Kapazitive Einspeisung in einen Hohlleiter; im rechten Bild Ansicht von oben

In einen Hohlleiter kann die Energie verschiedenartig ein- bzw. ausgekoppelt werden. Die für viele technische Anwendung bedeutende H₁₀-Welle wird durch eine im Abstand λ/4 vom geschlossenen Ende entfernten Einspeisepunkt angebrachte Stabantenne eingekoppelt. Bei der kapazitiven Einkopplung von einem Koaxialkabel aus, wie in der nebenstehenden Abbildung dargestellt, ist der Innenleiter ähnlich wie bei einer Stabantenne offen. Durch diese Anordnung erzwingt man ein Feldmaximum der eingekoppelten Welle am Einkopplungspunkt, womit sich die H₁₀-Welle nur in der einzig verbleibenden Richtung ausbreiten kann.

Bei der magnetischen Ankopplung einer Koaxialverbindung an den Hohlleiter ist der Innenleiter im Hohlleiter mit der hinteren Wandung kurzgeschlossen. Auch dabei wird ein Feldmaximum am Einspeisepunkt erzeugt.

Bei der Verbindung eines Hohlleiters mit anderen Geräten muss der elektrische Widerstand entlang des gesamten Umfangs sehr gering sein, da in der Wandung hohe Ströme fließen können. Ein einfacher Anpresskontakt kann den Übergangswiderstand nicht dauerhaft gering halten, deshalb verwendet man im Flansch eine λ/2-Transformationsleitung A-C, die einen Kurzschluss bei A in einen Kurzschluss bei C transformiert (siehe Sonderfall λ/2). Man wählt einen Hohlleitermodus, bei dem bei C ein Spannungsmaximum liegt (siehe mittleres Bild).

Da in der Mitte bei Punkt B nur geringe Ströme fließen, wirkt sich dort ein etwaiger Übergangswiderstand wenig aus. An dieser Stelle kann man sogar eine isolierende Gummiplatte einbauen, um den Hohlleiter mit Schutzgas füllen zu können. Dieses Prinzip der Resonanzdichtung wird auch eingesetzt, um die Tür eines Mikrowellenherdes hochfrequenztechnisch abzudichten.

Der Abschluss eines Hohlleiters kann reflexionsfrei mittels eines Wellensumpfes erfolgen.

Geschichte

Erste Ideen zu Hohlleitern und Koaxialkabeln gehen auf Joseph John Thomson und Oliver Lodge in den Jahren 1893 und 1894 zurück. Die erste mathematische Ausarbeitung der Vorgänge stammt von Lord Rayleigh, der um 1897 vorschlug, bei den damals schon bekannten Koaxialkabeln den Innenleiter zu entfernen, damit sich die elektromagnetische Welle, geführt nur durch die Außenwandung, darin ausbreiten könnte. Er beschrieb die Vorgänge durch Reflexionen der Welle an der Ummantelung, ähnlich wie es bei Lichtwellenleitern der Fall ist. Rayleigh war auch der Erste, der erkannte, dass jeder Hohlleiter eine untere Grenzfrequenz haben muss, die von seiner Abmessung bestimmt ist. Erste praktisch verwendete Hohlleiter, zunächst mit kreisförmigen Querschnitt, wurden 1932 von George Clark Southworth und J. F. Hargreaves gebaut.^[2] Größere Verbreitung erhielten Hohlleiter mit der aufkommenden militärischen Radartechnik im Zweiten Weltkrieg. Zivile Anwendungen, beispielsweise bei Nachrichtensatelliten, folgten in den Jahrzehnten danach.

Hohlleiter-Frequenzbänder

Ein Hohlleiter mit bestimmten Abmessungen wird jeweils nur in einem bestimmten Frequenzbereich mit weniger als einer Oktave Bandbreite sinnvoll benutzt. Unterhalb der unteren Grenzfrequenz ist keine Ausbreitung möglich und die elektromagnetische Welle wird blindgedämpft, oberhalb der oberen Frequenzgrenze sind neben der gewünschten Grundmode unerwünschte höhere Moden ausbreitungsfähig. Handelsübliche Rechteck-Hohlleiter sind unter anderem für die folgenden Frequenzbereiche erhältlich^[3]:

Mehrere Hohlleiter im Argonne National Laboratory

Frequenzbereich (GHz)	Band- bezeich- nung	Bezeichnung			Breite
Frequenzbereich (GHz)	Band- bezeich- nung	IEC 153 / DIN 47302	EIA	IEEE (WM)	(mm)	(Zoll)
0,77 … 1,14	UHF/L	R 9	WR 975		247,65	9,750
1,12 … 1,70	L	R 14	WR 650		165,10	6,500
1,7 … 2,6	LA	R 22	WR 430		109,22	4,300
2,2 … 3,3	LS	R 26	WR 340		086,36	3,400
2,60 … 3,95	S	R 32	WR 284		072,14	2,840
3,22 … 4,90	A	R 40	WR 229		058,17	2,290
3,95 … 5,85	G	R 48	WR 187		047,55	1,872
4,64 … 7,05	C	R 58	WR 159		040,39	1,590
5,85 … 8,20	J	R 70	WR 137		034,85	1,372
7,05 … 10,0	H	R 84	WR 112		028,50	1,122
8,20 … 12,4	X	R 100	WR 90		022,86	0,900
10,0 … 15,0	M	R 120	WR 75		019,05	0,750
12,4 … 18,0	P	R 140	WR 62		015,80	0,622
15,0 … 22,0	N	R 180	WR 51		012,95	0,510
18,0 … 26,5	K	R 220	WR 42		010,67	0,420
21,7 … 33,0		R 260	WR 34		008,64	0,340
26,5 … 40,0	R	R 320	WR 28		007,11	0,280
33,0 … 50,0	Q	R 400	WR 22		005,69	0,224
40,0 … 60,0	U	R 500	WR 19		004,78	0,188
50,0 … 75,0	V	R 620	WR 15		003,76	0,148
60,0 … 90,0	E	R 740	WR 12		003,048	0,120
75,0 … 110	W	R 900	WR 10	WM-2540	002,54	0,100
900 … 140	F	R 1200	WR 8	WM-2032	002,032	0,080
110 … 170	D	R 1400	WR 6	WM-1651	001,651	0,065
140 … 220		R 1800	WR 5	WM-1295	001,295	0,051
170 … 260		R 2200	WR 4	WM-1092	001,092	0,043
220 … 325		R 2600	WR 3	WM-864	000,864	0,034
260 … 400			WR 2.8	WM-710	000,710	0,02795
325 … 500	Y		WR 2.2	WM-570	000,570	0,02244
400 … 600			WR 1.9	WM-470	000,470	0,01850
500 … 750			WR 1.5	WM-380	000,380	0,01496
600 … 900			WR 1.2	WM-310	000,310	0,01220
750 … 1100			WR 1	WM-254	000,254	0,01000
900 … 1400				WM-200	000,200	0,007874
1100 … 1700			WR0.65	WM-164	000,164	0,006457
1400 … 2200				WM-130	000,130	0,005118
1700 … 2600				WM-106	000,106	0,004173
2200 … 3300				WM-86	000,086	0,003386
2600 … 4000				WM-71	000,071	0,002795
3300 … 5000				WM-57	000,057	0,002244

Dieser Tabelle liegt ein Breite-Höhe-Verhältnis von 2:1 zugrunde. Die unteren empfohlenen Übertragungsfrequenzen liegen im Mittel um das 1,26-fache über der sich aus der Breite ergebenden kritischen unteren Grenzfrequenzen, die oberen Übertragungsfrequenzen betragen im Mittel das 1,48fache der unteren empfohlenen Übertragungsfrequenzen. Der Faktor 1,86 (Mittelwert) der oberen Übertragungsfrequenzen zur jeweiligen kritischen unteren Grenzfrequenz sichert monomodige Ausbreitung (Wert < 2).

Zur WRxxx-Bezeichnung der Hohlleiter: Dabei wird die Breite des Hohlleiters in % eines Zolls (1 Zoll (inch) = 25,4 mm) ausgedrückt. Ein WR-28-Hohlleiter ist somit 28 % eines Zolls = 7,11 mm breit.

Hohlleiter in der Praxis

Hohlleiter werden verwendet:

im Mikrowellenherd (hier ist nur ein kurzes Stück zwischen Magnetron und Garraum vorhanden)
an Richtfunkanlagen und Radioteleskopen zur Antennenspeisung (siehe auch Hornstrahler)
in Satelliten zur Antennenspeisung und zur Speisung des Empfangsverstärkers
im Plasmagenerator als Verbindung zwischen den Magnetrons und der Plasmakammer
in Radargeräten zur Übertragung der hohen Sendeimpulsleistung zur Antenne und des empfangenen Echos zurück in den Empfänger
in Teilchenbeschleunigern zur Speisung der Hohlraumresonatoren.

Ein Leitungslüfter hält Feuchtigkeit aus der Umgebung fern, die die Anpassung des Hohlleiters verfälschen könnte.

Literatur

Horst Stöcker: Taschenbuch der Physik. 4. Auflage. Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4
Technik der Nachrichtenübertragung Teil 3 Drahtgebundene Nachrichtenübertragung – Leitungstechnik. Institut zur Entwicklung moderner Unterrichtsmethoden e. V., Bremen
Werner Bächtold: Lineare Elemente der Höchstfrequenztechnik. 2. überarbeitete Auflage, Hochschulverlag AG an der ETH Zürich, Zürich 1998, ISBN 3-7281-2611-X
Wilfried Plaßmann, Detlef Schulz (Hrsg.): Handbuch Elektrotechnik. 5. Auflage, Vieweg & Teubner Verlag, Wiesbaden 2009, ISBN 978-3-8348-0470-9.
Hans Fricke, Kurt Lamberts, Ernst Patzelt: Grundlagen der elektrischen Nachrichtenübertragung. B.G. Teubner Verlag, Stuttgart 1979.
Hans Heinrich Meinke, Friedrich-Wilhelm Gundlach: Taschenbuch der Hochfrequenztechnik. 5. überarbeitete Auflage. Bd. II. Springer Verlag, Berlin 1992, ISBN 3-540-54715-0.
Klaus W. Kark: Antennen und Strahlungsfelder. 6. Auflage, Springer Fachmedien, Wiesbaden 2017, ISBN 978-3-658-13964-3.

Weblinks

Commons: Hohlleiter – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Hohlleiter – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Quasioptische Ableitung der Felder der Hohlleiterwellen (abgerufen am 14. Juli 2017)
Übersicht Hohlleiter (abgerufen am 14. Juli 2017)
Hochfrequenztechnik I Hohlleiter (abgerufen am 14. Juli 2017)
Moden bei der Wellenausbreitung (abgerufen am 14. Juli 2017)

Einzelnachweise

↑ Vector Network Analyzer Extension Modules (VNAX), vadiodes.com, abgerufen am 17. Oktober 2022.
↑ T.K. Sarkar, Robert Mailloux, Arthur A. Oliner, M. Salazar-Palma, Dipak L. Sengupta: History of Wireless. John Wiley & Sons, 2006, ISBN 0-471-78301-3, S. 90 und 129.
↑ Waveguide standards. In: Flann Microwave. Abgerufen am 17. Oktober 2022 (britisches Englisch).

[1] Vector Network Analyzer Extension Modules (VNAX), vadiodes.com, abgerufen am 17. Oktober 2022.

[histwir1-2] T.K. Sarkar, Robert Mailloux, Arthur A. Oliner, M. Salazar-Palma, Dipak L. Sengupta: History of Wireless. John Wiley & Sons, 2006, ISBN 0-471-78301-3, S. 90 und 129.

[3] Waveguide standards. In: Flann Microwave. Abgerufen am 17. Oktober 2022 (britisches Englisch).

[1]

[2]

[3]

Hohlleiter

Inhaltsverzeichnis

Physikalischer Hintergrund