Karnaugh-Veitch-Diagramm

Das Karnaugh-Veitch-Diagramm (bzw. das Karnaugh-Veitch-Symmetrie-Diagramm, die Karnaugh-Tafel oder der Karnaugh-Plan), kurz KV-Diagramm, KVS-Diagramm oder K-Diagramm (englisch Karnaugh map), dient der übersichtlichen Darstellung und Vereinfachung Boolescher Funktionen in einen minimalen logischen Ausdruck. Es wurde 1952 von Edward W. Veitch [viːtʃ] entworfen und 1953 von Maurice Karnaugh [ˈkɑːɹnɔː] zu seiner heutigen Form weiterentwickelt.

Eigenschaften

Mit einem KV-Diagramm lässt sich jede beliebige disjunktive Normalform (DNF) in einen minimalen disjunktiven logischen Ausdruck umwandeln. Der Vorteil gegenüber anderen Verfahren ist, dass der erzeugte Term (meist) minimal ist. Sollte der Term noch nicht minimal sein, ist eine weitere Vereinfachung durch Anwenden des Distributivgesetzes (Ausklammern) möglich. Das Umwandeln beginnt mit dem Erstellen einer Wahrheitstafel, aus der dann die DNF abgeleitet wird, die dann wiederum direkt in ein KV-Diagramm umgewandelt wird.

Da sich die den benachbarten Feldern zugehörigen Minterme jeweils in nur einer Variablen A durch Negierung unterscheiden, wird diese (nach Ausklammern mit dem Distributivgesetz und Anwendung von $A\vee \neg A=1$ ) aus dem Term, der die zusammenzufassenden Nachbarfelder beschreibt, eliminiert. Auf dieser Regel basiert die Reduzierung der Gruppen.

Die inverse Funktion ${\bar {F}}$ findet man durch Vertauschen von „1“ und „0“ im KV-Diagramm.

Ein KV-Diagramm ist ebenfalls nützlich, um Hazards festzustellen und zu eliminieren.

Das Ausfüllen des KV-Diagramms

Ein KV-Diagramm für n Eingangsvariablen hat 2ⁿ Felder (siehe Beispiel). Das KV-Diagramm wird mit den Variablen an den Rändern beschriftet. Dabei kommt jede Variable in negierter und nicht-negierter Form vor. Die Zuordnung der Variablen zu den einzelnen Feldern kann dabei beliebig erfolgen, jedoch ist zu beachten, dass sich horizontal und vertikal benachbarte Felder nur in genau einer Variablen unterscheiden dürfen (Gray-Code). Mit Hilfe der Wahrheitstabelle der zu optimierenden Funktion wird in die einzelnen Felder eine 1 eingetragen, wenn ein Minterm der Funktion vorliegt, andernfalls eine 0. Ein Minterm $m$ der Funktion liegt dann vor, wenn gilt

m({\underline {X}})=1\Rightarrow F({\underline {X}})=1

,

wobei ${\underline {X}}$ der Vektor der Eingangsvariablen ist. In einer disjunktiven Normalform gilt dies für jeden Konjunktionsterm, der 1 liefert, da dann auch die Gesamtdisjunktion und folglich auch die Funktion 1 liefert.

KV-Diagramme eignen sich für die Vereinfachung von Funktionen mit maximal ca. 4–6 Eingangsvariablen; bis 4 Variablen sind sie übersichtlich.

Vereinfachung

Sind weniger Felder des KV-Diagramms mit 1 als mit 0 belegt, so wählt man die Minterm-Methode, andernfalls die Maxterm-Methode.

Minterm-Methode

Man versucht, möglichst viele horizontal und vertikal benachbarte Felder, die eine 1 enthalten (Minterme) zu rechteckigen zusammenhängenden Blöcken (Päckchen) zusammenzufassen. Als Blockgröße sind alle Potenzen von 2 erlaubt (1, 2, 4, 8, 16, 32, …). Dabei sind alle 1-Felder mit Blöcken zu erfassen.
Ein Block kann unter Umständen über den rechten bzw. unteren Rand des Diagramms fortgesetzt werden. Dies erklärt sich folgendermaßen: KV-Diagramme für drei Variablen müssen im Grunde als Zylinder verstanden werden. Die Felder ganz links und ganz rechts bzw. oben und unten sind also benachbart. KV-Diagramme für vier Variablen müssen im Grunde als Torus („Donut-Form“) verstanden werden; die vier Ecken des quadratisch gezeichneten KV-Diagrammes sind benachbart. Noch komplexere Nachbarschaftsbeziehungen gelten für 5 oder mehr Variablen. Da multidimensionale Gebilde zeichnerisch schwierig zu handhaben sind, wählt man die Darstellung in der Ebene, muss dann aber die Nachbarschaftsbeziehungen im Sinn behalten.
Von den ermittelten Blöcken sind so viele auszuwählen, dass alle 1-Felder überdeckt werden. Bei vielen Schaltfunktionen sind das alle zusammengefassten Blöcke, es kommt jedoch nicht selten vor, dass es Alternativen gibt. Dann besteht bei gleich großen Blöcken die freie Auswahl, andernfalls sind die größeren Blöcke zu wählen, da sie zu den kleineren (da stärker zusammengefassten) Termen führen.
Die gebildeten und ausgewählten Blöcke/Päckchen wandelt man nun in Konjunktionsterme um. Dabei werden Variablen innerhalb eines Blockes, die in negierter und nicht negierter Form auftreten, weggelassen.
Diese UND-Verknüpfungen werden durch ODER-Verknüpfungen zusammengefasst und ergeben eine disjunktive Minimalform.

Maxterm-Methode

Die Maxterm-Methode unterscheidet sich von der Minterm-Methode lediglich in folgenden Punkten:

Statt Einsen werden Nullen zu Päckchen zusammengefasst.
Ein Päckchen bildet einen Disjunktionsterm (ODER-Verknüpfungen statt eines Konjunktionsterms).
Die Disjunktionsterme werden konjunktiv (mit UND) verknüpft.
Die Variablen werden zusätzlich einzeln negiert.

Ringsummen-Methode

Es besteht auch die Möglichkeit, eine so genannte Ringsummen-Normalform aus einem KV-Diagramm abzulesen. Da bei der Ringsummen-Normalform nur Minterme ohne Negation auftreten, dürfen nur Blöcke gebildet werden, die keine Negation enthalten. Durch eine mehrfache Überdeckung der Blöcke muss erreicht werden, dass für alle Nullen eine gerade Anzahl Überdeckungen und für alle Einsen eine ungerade Anzahl Überdeckungen vorliegen. Hierbei wird die Regel $T\oplus T=0$ bzw. $T\oplus T\oplus T=T$ benutzt. Jeder Block liefert einen Minterm, die mittels XOR verknüpft werden. Die Ringsummen-Normalform ist bis auf die Reihenfolge der Minterme eindeutig.

Don’t-Care-Zustände

Häufig gibt es Boolesche Funktionen mit Wahrheitstabellen, in denen nicht für jede Kombination der Eingangsvariablen ein Wert der Ausgangsvariablen definiert sein muss. Man nennt solche Ausgangszustände Don’t-Care-Terme und bezeichnet sie mit $X$ , da sie sowohl den Wert 1 als auch 0 annehmen können. Diese $X$ -Felder dürfen als 1 oder 0 angesehen werden, um in der Minterm- oder Maxterm-Methode Blöcke von Einsen oder Nullen zu vervollständigen. Ein gutes Beispiel dafür ist die Dekodierung einer binär codierten Dezimalzahl (BCD). Hier spielen nur die Zahlen 0 bis 9 eine Rolle, die sogenannten Pseudotetraden dürfen ein beliebiges Ergebnis liefern, sind also Don’t-Care-Terme.

KV-Diagramm bei mehreren Ausgängen

Wenn eine Digitalschaltung mehrere Ausgänge hat, die Wahrheitstabelle also mehrere Ergebnisspalten hat, dann muss für jeden Ausgang ein eigenes KV-Diagramm erstellt werden.

Beispielsweise hat ein 1-aus-n-Decoder die nebenstehende Wahrheitstabelle und für seine 4 Ausgänge die 4 nebenstehenden KV-Diagramme.

Eingabe				Ausgabe
Zahl 1		Zahl 2		$A<B$	$A=B$	$A>B$
$A_{1}$	$A_{0}$	$B_{1}$	$B_{0}$	$X$	$Y$	$Z$
0	0	0	0	0	1	0
0	0	0	1	1	0	0
0	0	1	0	1	0	0
0	0	1	1	1	0	0
0	1	0	0	0	0	1
0	1	0	1	0	1	0
0	1	1	0	1	0	0
0	1	1	1	1	0	0
1	0	0	0	0	0	1
1	0	0	1	0	0	1
1	0	1	0	0	1	0
1	0	1	1	1	0	0
1	1	0	0	0	0	1
1	1	0	1	0	0	1
1	1	1	0	0	0	1
1	1	1	1	0	1	0

Ein weiteres Beispiel für mehrere Ausgänge ist ein 2+2-Bit-Komparator. Er hat vier Eingangsvariablen und drei Ausgangvariablen. Die Zahl A besteht aus 2 Bit ( $A_{1}$ und $A_{0}$ ) und die Zahl B besteht aus 2 Bit ( $B_{1}$ und $B_{0}$ ). Je nachdem, ob „ $A<B$ “, „ $A=B$ “ oder „ $A>B$ “ geben die drei Ausgänge $(X,Y,Z)$ eine 1 oder 0 aus.

Die dazugehörige Wahrheitstabelle ist rechts. Die Bilder 5-2 bis 5-4 zeigen die 3 KV-Diagramme für die 3 Ausgänge.

Normalformen

A	B	C	D	X
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	1

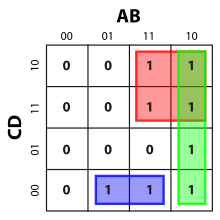
Üblicherweise werden Gruppen für die Einsen gebildet (Bild 6-2). Die Einsen leiten sich aus der Disjunktiven Normalform (DNF) ab. Es gibt aber auch die Möglichkeit, Gruppen aus den Nullen zu bilden (in Bild 6-1 und den nachfolgenden sind die Nullen nicht extra eingezeichnet, aber trotzdem vorhanden). Die Nullen stehen für die Konjunktive Normalform (KNF).

Die DNF lautet: ¬AB¬C¬D ∨ ¬AB¬CD ∨ ¬ABCD ∨ AB¬C¬D ∨ AB¬CD ∨ ABCD.

Die KNF lautet: (A∨B∨C∨D) ∧ (A∨B∨C∨¬D) ∧ (A∨B∨¬C∨D) ∧ (A∨B∨¬C∨¬D) ∧ (A∨¬B∨¬C∨D) ∧ (¬A∨B∨C∨D) ∧ (¬A∨B∨C∨¬D) ∧ (¬A∨B∨¬C∨D) ∧ (¬A∨B∨¬C∨¬D) ∧ (¬A∨¬B∨¬C∨D).

Die DNF wird aus der Tabelle ausgelesen, indem jede Zeile mit dem Ausgabewert „Eins“ aufgeschrieben wird. Die Eingangsvariablen für die eine Null steht, werden in negierter Form genommen. Alle Terme für die Zeilen (im vorliegenden Beispiel 6 Zeilen) werden durch „∨“ verbunden.

Für die KNF werden alle Zeilen mit dem Ausgabewert „Null“ rausgeschrieben, wobei Eingangsvariablen für die eine „Eins“ steht, in negierter Form genommen werden. Alle Terme für die Zeilen (im vorliegenden Beispiel 10 Zeilen) werden durch „∧“ verbunden, die Literale selber werden durch „∨“ verbunden.

Fehler in Bild 6-2: Das Minimalpolynom lautet: B (D ∨ ¬C), da das rote Zweier-Kästchen nach oben hin zu einem Vierer-Kästchen erweitert werden kann, wodurch mehr Literale wegfallen und das endgültige Minimalpolynom der Länge 4 (BD ∨ B¬C) entsteht. Wichtig hierbei zu beachten ist, dass dadurch zwar zwei einschlägige Indizes mehrfach verwendet werden, dies aber sowohl erlaubt, als auch nötig ist, um das Minimalpolynom zu bilden.

Gesetzmäßigkeiten bei der Reduzierung

Durch die Zusammenfassung zu einer Gruppe der Größe 2ⁿ reduziert sich der logische Ausdruck um n Variablen. Das ist unabhängig davon, welche Lage oder Form die Gruppe hat oder ob sie über die Ränder hinwegreicht. Das ist auch unabhängig davon, ob es sich um ein 2×2, 2×4, 4×4 oder 4x4x4 KV-Diagramm handelt.

Eine Achtergruppe (2³) reduziert sich um 3 Variablen (n = 3) – Bild 9-1.
Eine Vierergruppe (2²) reduziert sich um 2 Variablen (n = 2) – Bild 9-2 und 9-3.
Eine Zweiergruppe (2¹) reduziert sich um 1 Variable (n = 1) – Bild 9-4 und 9-5.
Eine Einergruppe (2⁰) reduziert sich um Null Variablen (n = 0) – Bild 9-6.

Regeln für die Gruppenbildung

Benachbarte Felder, in die eine Eins eingetragen ist, werden zu Gruppen zusammengefasst.
Eine Gruppe darf keine Felder mit Nullen enthalten. (Oft werden die Nullen nicht mitgeschrieben und die Felder leer gelassen. In diesem Fall darf eine Gruppe keine leeren Felder enthalten.)
Alle Einsen müssen in Gruppen zusammengefasst werden.
Benachbarte Felder mit Einsen werden zu einer Gruppe zusammengefasst. (Felder, die sich an den Ecken berühren, diagonal, zählen nicht als benachbart.)
Die Gruppen müssen so groß wie möglich sein.
Es müssen so wenig Gruppen wie möglich gebildet werden.
Die Gruppen dürfen nur Größen haben, die Zweierpotenzen entsprechen (1, 2, 4, 8, 16, 32, 64 …).
Die Gruppen müssen rechteckige Blöcke sein.
Die Gruppen dürfen sich überlappen.
Die Gruppen dürfen über die Ränder hinweggehen.
Zwei Gruppen dürfen nicht exakt die gleichen Einsen umfassen.
Es darf keine Gruppe vollständig von einer anderen Gruppe umschlossen werden.

Zusammenfassung: Man sucht eine vollständige Überdeckung der Einsen mit möglichst großen rechteckigen Blöcken.

KV-Tafeln für 2 und 4 Variablen

Wer häufig mit dem KV-Diagramm arbeitet, wünscht sich eine Methode, ein KV-Diagramm schnell ausfüllen zu können.

Dies wird bei oben dargestellter Anordnung bei den vier Eingangsvariablen A, B, C und D durch folgende Anordnung erreicht:

Bild 3: Verdeutlicht die logischen Werte der 16 Felder; wenn man aus einer Wahrheitstabelle zeilenweise die DNF in das KV-Diagramm überträgt, dann erfolgt die Eintragung in der Reihenfolge der roten Zahlen
Bild 4: Die roten Zahlen erleichtern die zeilenweise Zuordnung der Wahrheitstabelle zu den einzelnen Feldern; die Reihenfolge hängt von der konkreten Beschriftung des KV-Diagramms ab; die Nummerierung stellt eine Arbeitserleichterung bei umfangreicher Verwendung von KV-Diagrammen dar

Dabei wird jedem Feld ihre Wertigkeit zugeordnet. Bei 4 Signalen sind dies 16 Einträge:

0000 = 0, 0001 = 1, 0010 = 2, …, 1110 = 14, 1111 = 15

Auf diese Weise kann das KV-Diagramm sehr schnell ausgefüllt werden. Es sind neben oben dargestellter Anordnungen aber auch Variationen der Anordnung der Eingangsvariablen A, B, C und D möglich. Dadurch ergeben sich andere Aufteilungen der Wertigkeiten in der Matrix.

Insgesamt ergeben sich für KV-Diagramme mit 4 Eingängen die folgende Anzahl an unterschiedlichen Kombinationsmöglichkeiten zur Zusammenfassung von Gruppen/Blöcken:

16er Blöcke: max. 1

8er Blöcke: max. 8

4er Blöcke: max. 24

2er Blöcke: max. 32

1er Blöcke max. 16

Mengendiagramm

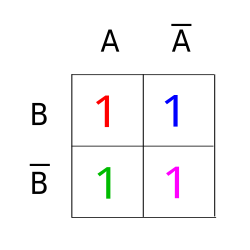
Das Karnaugh-Veitch-Diagramm ist eine abgewandelte, abstrakte Form des Venn-Diagramms, bei dem im Sinne der Mengenalgebra die Teilmengen von Mintermen betrachtet werden können, die an der Funktion beteiligt sind.

Die Bilder 1 bis 4 zeigen ein Venn-Diagramm und das äquivalente KV-Diagramm.

2 Variablen
Bild 1: KV-Diagramm
Bild 2: Venn-Diagramm

4 Variablen
Bild 3: KV-Diagramm
Bild 4: Venn-Diagramm

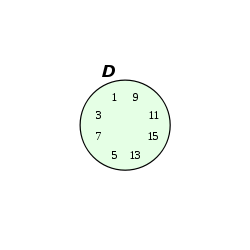
Die Bilder 5 bis 8 zeigen noch einmal die einzelnen Teilmengen, aus denen sich das Venn-Diagramm in Bild 4 zusammensetzt.

4 Variablen
Bild 5: Teilmenge im Venn-Diagramm
Bild 6: Teilmenge im Venn-Diagramm
Bild 7: Teilmenge im Venn-Diagramm
Bild 8: Teilmenge im Venn-Diagramm

Veranschaulichung durch Hyper-Einheitswürfel

Boolesche Funktionen mit n Variablen lassen sich grafisch mittels Einheitswürfeln der Dimension n veranschaulichen. Würfel beliebiger Dimension bezeichnet man auch als Hyperwürfel. Da Karnaugh-Diagramme selbst eine spezielle Darstellungsform für Boolesche Funktionen sind, überrascht es nicht, dass sich zwischen Hyper-Einheitswürfeln und Karnaugh-Diagrammen ein anschaulicher Zusammenhang herstellen lässt. Und zwar entsprechen Karnaugh-Diagramme für n Variablen umkehrbar eindeutig den Hyper-Einheitswürfeln der Dimension n. Die Ecken-Koordinaten des Hyperwürfels entsprechen dabei den dualen Nummern der Felder im Karnaugh-Diagramm.

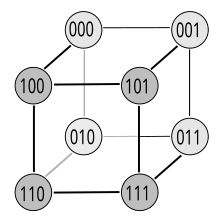
Bild 3-2 zeigt den Einheitswürfel für 3 Variablen. Das entspricht einem 2×4 KV-Diagramm. Das KV-Diagramm in Bild 3-3 ist in Bild 3-4 entsprechend markiert (grüne Ebene). Die Knoten (Eckpunkt oder Kreise) am Hyper-Einheitswürfel entsprechen jeweils einem Feld im KV-Diagramm. Die Übergänge (Nachbarschaft der Felder) sind durch die Kanten des Würfels symbolisiert. Beim Wandern auf der Kante entsteht ein Gray-Code. Auf jeder Kante ändert sich genau 1 Bit. Eine wesentliche Eigenschaft ist, dass sich die Gray-Codes für zwei benachbarte Zahlen nur um 1 Ziffer, bei Binärcode also 1 Bit, unterscheiden (Hamming-Distanz).

Das KV-Diagramm hat so viele Nachbarschaften, wie der Würfel Kanten hat. Bild 3-5 zeigt eine ebene Darstellung des Hyper-Einheitswürfels. Ohne seine innere Struktur der Übergänge zu ändern lässt sich der Würfel in beliebige Richtungen „umstülpen“, wie in der Animation in Bild 3-9 dargestellt ist. So ist zu erklären, warum es KV-Diagramme mit verschiedenen Anordnungen der Variablen gibt (Randbeschriftung). Sie wurden praktisch wie ein Würfel „umgestülpt“.

Für das KV-Diagramm mit 2 Variablen (2×2 Feld) ergibt sich ein einfacherer Hyper-Einheitswürfel (Bild 3-6). Bei 1 Variable ist der „Würfel“ trivial (Bild 3-7). Mit zunehmenden Variablen steigt die Anzahl der Kanten allerdings exponentiell an. So gibt es bei 4 Variablen (Bild 3-8) bereits 32 Kanten.

Bild 3-7

Erweiterung des Symmetriediagramms für mehr als 4 Eingangsvariablen

Ein Nachteil der ursprünglichen Variante des KV-Diagramms ist, dass es für mehr als 4 Eingangsvariablen nicht geeignet ist. Um mit einer beliebigen Zahl von Eingangsvariablen zu arbeiten, kann die verallgemeinerte Form des Symmetriediagramms verwendet werden.^[1]

Bei diesem Verfahren wird die Entstehung eines KV-Diagramms mit n Eingangsvariablen dadurch erklärt, dass ein KV-Diagramm mit n-1 Eingangsvariablen gespiegelt und dadurch verdoppelt wird. Daher die Bezeichnung „Symmetriediagramm“. Die neu entstehende Hälfte des KV-Diagramms entspricht dann der neu hinzugekommenen Eingangsvariable in nicht-negierter Form, während die bereits bestehende Hälfte der Eingangsvariable in negierter Form entspricht.

Durch Spiegelung eines Symmetriediagramms mit n Eingangsvariablen kann auf diese Art und Weise eines mit n+1 Eingangsvariablen erzeugt werden, so dass die Anzahl der Eingangsvariablen selbst im Zweidimensionalen nicht beschränkt ist.

Auch die Gruppenbildung aus zusammenhängenden, rechteckigen Blöcken im herkömmlichen KV-Diagramm wird über die Spiegelung erklärt:

Jede denkbare Gruppe aus Feldern in einem KV-Diagramm mit n Eingangsvariablen, die einen Minterm oder Maxterm darstellt, kann durch die Spiegelung und/oder das Beibehalten einer Gruppe im KV-Diagramm mit n-1 Eingangsvariablen erzeugt werden. So wird zum Beispiel der Minterm ¬AB (in der Zeichnung rot markiert) dadurch erzeugt, dass

bei der ersten Spiegelung die ursprüngliche Gruppe nicht mitgespiegelt (sondern beibehalten),
bei der zweiten Spiegelung die Gruppe mitgespiegelt und die bestehenden Felder nicht beibehalten und
bei der dritten Spiegelung die Gruppe mitgespiegelt und die bestehenden Felder gleichzeitig beibehalten werden.

Die Bedingung dafür, dass mehrere Felder eine Gruppe bilden können, ist daher nicht, dass es sich um zusammenhängende rechteckige Blöcke handelt, sondern ob es möglich ist, eine entsprechende Gruppe durch Spiegelung und Beibehalten zu erzeugen. Bei KV-Diagrammen mit bis zu 4 Eingangsvariablen führt diese Bedingung aber zu den gleichen Gruppen wie die Regel, dass es sich bei den Gruppen um zusammenhängende Rechtecke handeln muss. Dies ist allerdings ab 5 Eingangsvariablen nicht mehr der Fall, wie man anhand des folgenden Beispiels mit 6 Eingangsvariablen sehen kann.

Der blau markierte Block stellt keinen gültigen Block (der einen Minterm darstellt) dar, obwohl alle Regeln für eine Blockbildung in einem herkömmlichen KV-Diagramm erfüllt wären. Die rot markierte Gruppe aus Feldern entspricht dem Minterm ¬AB¬D; es ist somit eine gültige Gruppe. Es handelt sich dabei aber eindeutig nicht um einen zusammenhängenden Block.

Die Anwendung des Verfahrens für mehr als 4 Eingangsvariablen ist allerdings schwerer als die Anwendung mit maximal 4 Eingangsvariablen, da nicht zusammenhängende Gruppen von Einsen dem Anwender nicht so leicht auffallen wie zusammenhängende Rechtecke aus Einsen.

Siehe auch

Verfahren nach Quine und McCluskey – bei mehr als 5 Eingangsvariablen besser geeignet als das KV-Diagramm
Schaltalgebra
Buchberger-Algorithmus
Disjunktive Normalform
Konjunktive Normalform

Literatur

Maurice Karnaugh: The Map Method for Synthesis of Combinational Logic Circuits. Transactions of the AIEE, Vol. 72, No. 9 (1953), S. 593–599.
Edward W. Veitch: A chart method for simplifying truth functions. Proc. Assoc. for Computing Machinery, Pittsburgh Mai 1952, S. 127–133.
Klaus Beuth: Digitaltechnik. Vogel Buchverlag, 2001, ISBN 3-8023-1755-6 (Kapitel 5).
Günter Wellenreuther, Dieter Zastrow: Steuerungstechnik mit SPS: Von der Steuerungsaufgabe zum Steuerprogramm. Vieweg+Teubner Verlag, 1998, ISBN 3-528-44580-7 (Kapitel 4.5.2).
Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, 2002, ISBN 3-540-42849-6.
Manfred Seifart, Helmut Beikirch: Digitale Schaltungen. 5. Auflage. Technik, 1998, ISBN 3-341-01198-6.

Weblinks

Wikibooks: Karnaugh-Veitch-Diagramm: Beispiele (Teil 1) – Lern- und Lehrmaterialien

Commons: Karnaugh maps – Sammlung von Bildern, Videos und Audiodateien

Peter Fischer, Universität Heidelberg: Karnaugh - Diagramme
Heiko Falk, Universität Ulm: Grundlagen der Rechnerarchitektur, Seite 56 bis 80
Kostenloses Lernprogramm. Lernziele: Aufstellen von Wahrheitstabellen und der disjunktiven Normalform (DNF), Vereinfachen von Schaltnetzen mit KV-Tafeln für 2 bis 5 Variable.
JavaScript zum Bearbeiten von KV-Diagrammen der Universität Marburg

Einzelnachweise

↑ Hans Martin Lipp, Jürgen Becker: Grundlagen der Digitaltechnik. Oldenbourg-Verlag, München 2011, ISBN 978-3-486-59747-9.

[1] Hans Martin Lipp, Jürgen Becker: Grundlagen der Digitaltechnik. Oldenbourg-Verlag, München 2011, ISBN 978-3-486-59747-9.

[1]

Karnaugh-Veitch-Diagramm

Inhaltsverzeichnis

Eigenschaften