Reluktanzkraft


Die Reluktanzkraft oder auch Maxwellsche Kraft entsteht aufgrund der Änderung des magnetischen Widerstands, der auch als Reluktanz bezeichnet wird. Die Reluktanzkraft wirkt immer so, dass sich der magnetische Widerstand verringert und die Induktivität steigt und ist der Magnetostatik zuzurechnen.
Entdecker der Reluktanzkraft war 1981 K. Hanns Meyer mit seinem Artikel Reluktanzkraft in einem Lautsprecherantrieb.[1]
Diese Eigenschaft wird bei einigen Typen von elektrischen Maschinen benutzt, zum Beispiel bei geschalteten Reluktanzmaschinen, Transversalflussmaschinen, dem Synchron-Reluktanzmotor oder elektromagnetischen Lagern.
Eine verwandte Kraft ist die Lorentzkraft, welche die Kraftwirkung auf eine bewegte elektrische Ladung in einem äußeren elektromagnetischen Feld beschreibt.
Beweglicher Kern
[Bearbeiten | Quelltext bearbeiten]Die Reluktanzkraft kann hergeleitet werden aus der Änderung der Energie , die sich bei einer infinitesimalen Verschiebung des beweglichen Stücks zur Seite ergibt:
- ,
- .
Darin ist
- der elektrische Strom und
- die Induktivität.
Die Induktivität eines magnetischen Kreises mit Luftspalt ist gegeben durch
mit
- der Anzahl der Spulenwindungen
- dem magnetischen Widerstand , wobei für die Näherung der magnetische Widerstand des Kerns gegenüber demjenigen des Luftspalts vernachlässigt wird
- der magnetischen Feldkonstante
- der Stirnfläche des magnetischen Kreises am Luftspalt, durch welche die Feldlinien des magnetischen Feldes hindurchtreten
- der Summe der Größe beider Luftspalte.
Die (idealisierte) Fläche, die für den magnetischen Kreis zur Verfügung steht, ergibt sich zu
Dabei ist die Richtung der Auslenkung unerheblich, daher die Betragsstriche. Die Größe bezeichnet die Tiefe.
Einsetzen liefert
so dass auf den beweglichen Teil des ausgelenkten Kerns eine Kraft
wirkt, die ihn zur Mitte hin zieht. Diese ist unabhängig von der Größe der Auslenkung, außer wenn die obige Ableitung ihre Gültigkeit verliert. Dies ist der Fall, wenn zu groß wird.
Veränderlicher Luftspalt
[Bearbeiten | Quelltext bearbeiten]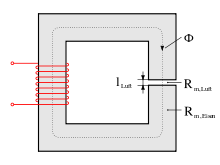
Analog zu oben gilt
- .
Für die Induktivität gilt auch hier näherungsweise
- .
Mit der Potenzregel erhält man
- .
Einsetzen in die Formel für liefert das Ergebnis:
- .
Da bei einer Verkleinerung des Luftspalts die Induktivität steigt, wirkt die Reluktanzkraft in diese Richtung. Die Kraft nimmt mit der Breite des Luftspalts ab. Das Maximum der Reluktanzkraft ist erreicht, wenn der Luftspalt gegen null geht. Allerdings gilt bei sehr kleinem Luftspalt die Näherungsformel für die Induktivität nicht mehr, da dann der magnetische Widerstand des Kerns nicht mehr vernachlässigt werden kann.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Hans-Dieter Stölting, Eberhard Kallenbach (Hrsg.): Handbuch Elektrische Kleinantriebe. 3. Auflage. Hanser, ISBN 3-446-40019-2, S. 460.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Maxwellkraft auf www.energie.ch
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Elektrotechnische Zeitschrift; 3/81; S. 284

























