Gemischt-ganzzahlige Optimierung
In der gemischt-ganzzahligen Optimierung (englisch mixed-integer optimization oder mixed-integer programming) werden Optimierungsprobleme untersucht, die kontinuierliche und ganzzahlige Entscheidungsvariablen besitzen. Sie ist ein Teilgebiet der mathematischen Optimierung mit Anwendungen in der Automobilindustrie, Chemieindustrie, Energiewirtschaft, Finanzindustrie, Gesundheitswesen, Lebensmittelindustrie, Papierindustrie, Supply Chain Management (insbes. Transport, Logistik und Produktion), Statistik, Machine Learning und der Telekommunikation.[1][2][3][4][5]
Mathematische Definition
[Bearbeiten | Quelltext bearbeiten]Ein gemischt-ganzzahliges (nichtlineares) Optimierungsproblem (engl.: mixed-integer (nonlinear) program oder mixed-integer (nonlinear) problem, kurz: MINLP) ist ein Optimierungsproblem, welches aus einer Zielfunktion, kontinuierlichen und ganzzahligen Entscheidungsvariablen und einer zulässigen Menge besteht. Die zulässige Menge wird durch Gleichungen und Ungleichungen beschrieben, wobei untere und obere Schranken an die Entscheidungsvariablen als besonders einfach zu handhabende Nebenbedingungen oft separat aufgeführt werden. Mathematisch formuliert lautet ein MINLP mit Entscheidungsvariablen
Die zu minimierende Zielfunktion sowie die die Restriktionen definierenden Funktionen und dürfen beliebige nichtlineare Funktionen sein, deren stetige Differenzierbarkeit jedoch in der Literatur meistens vorausgesetzt wird. Für die Schranken an die Entscheidungsvariable gilt bzw. . In der Menge sind die Indizes der ganzzahligen Variablen hinterlegt und die Mengen und dienen der Indizierung der auftretenden Ungleichungs- und Gleichungsrestriktionen. Natürlich können alle auftretenden Indexmengen auch leer sein.
Einfache Beispiele
[Bearbeiten | Quelltext bearbeiten]Die folgenden Beispiele sind der Literatur entnommen.[2]
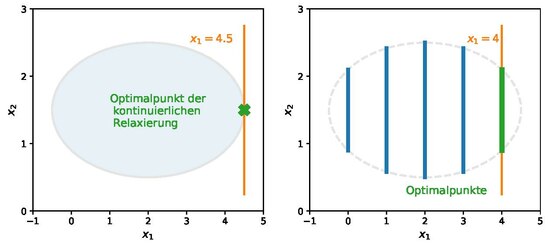
Minimierung über einer elliptischen gemischt-ganzzahligen zulässigen Menge
[Bearbeiten | Quelltext bearbeiten]Zu lösen ist folgendes MINLP mit einer linearen Zielfunktion und nichtlinearen Nebenbedingungen sowie einer Ganzzahligkeitsbedingung an , wohingegen eine kontinuierliche Entscheidungsvariable ist.Eine Minimierung auf der kontinuierlichen Relaxierung der zulässigen Menge – also der Menge die entsteht, wenn die Ganzzahligkeitsbedingung ignoriert wird – ergibt den eindeutigen Optimalpunkt . Wird jedoch berücksichtigt, dass ganzzahlig sein muss, so sind alle zulässigen Punkte mit optimal.
Gemischt-ganzzahlige Modellierung einer Menge mit disjunktiver Struktur
[Bearbeiten | Quelltext bearbeiten]Gesucht ist eine gemischt-ganzzahlige Beschreibung der Menge , die alle reellen Zahlen zwischen 0 und 10 enthält, deren Abstand zu 5 größer oder gleich 2 ist. Zunächst wird notiert, dass eine solche Zahl zwischen 0 und 3 oder zwischen 7 und 10 liegen muss. Es gilt also und das auftretende logische Oder, das auch unter dem Namen Disjunktion bekannt ist, ist eine logische Verknüpfung. Da sich logische Verknüpfungen durch Binärvariablen modellieren lassen, wird eine solche Variable eingeführt, um folgendes System linearer Ungleichungen zu erhalten:Durch Fallunterscheidungen lässt sich nun überprüfen, dass das Ungleichungssystem tatsächlich äquivalent zur Menge ist. Für gilt und , also insgesamt . Für hingegen reduziert sich das System zu und , also .
Ausgewählte Anwendungen
[Bearbeiten | Quelltext bearbeiten]- Alle kombinatorischen Optimierungsprobleme, wie etwa das Rucksackproblem, das Problem des Handlungsreisenden oder das Bin-Packing-Problem
- Zahlreiche Optimierungsprobleme in der Energiewirtschaft wie etwa die Kraftwerkseinsatzoptimierung (engl. unit commitment problem)[6]
- Scheduling-Probleme wie etwa die Maschinenbelegungsplanung in der Produktion[7]
- Transportlogistik, zum Beispiel das Fleet Assignment Problem in der Luftfahrtindustrie[8], und zahlreiche Varianten der Tourenplanung (engl. vehicle routing problem)[3]
- Das Sparse Regression Problem, robuste Regression und andere Probleme der Statistik und des Machine Learnings[9]
Klassifikation von gemischt-ganzzahligen Optimierungsproblemen
[Bearbeiten | Quelltext bearbeiten]Je nach mathematischer Struktur unterscheidet man zwischen verschiedenen Klassen gemischt-ganzzahliger Optimierungsprobleme. Der Vollständigkeit halber sei erwähnt, dass für , also im Fall ohne Ganzzahligkeitsbedingungen, das MINLP zu einem kontinuierlichen nichtlinearen Optimierungsproblem (NLP) wird. Im Folgenden gelte also stets .
- Falls die Zielfunktion , sowie alle die Nebenbedingungen beschreibenden Funktionen und für alle und linear sind, spricht man von einem gemischt-ganzzahligen linearen Optimierungsproblem (MILP oder nur MIP).
- Ein MILP ohne kontinuierliche Entscheidungsvariablen ist ein sogenanntes ganzzahliges lineares Optimierungsproblem (ILP).
- Falls und/oder beliebig viele der Nebenbedingungen beschreibenden Funktionen und quadratisch sind, spricht man von einem gemischt-ganzzahligen quadratischen Optimierungsproblem (MIQP). Manchmal wird dies in der Literatur noch weiter unterschieden, sodass Probleme mit quadratischer Zielfunktion und linearen Restriktionen als MIQP und Optimierungsprobleme mit (teilweise) quadratischen Restriktionen als MIQCP (engl.: mixed-integer quadratically constrained program) bezeichnet werden.
- Falls die Nichtlinearität eines gemischt-ganzzahligen Optimierungsproblems „schlimmer“ als quadratisch ist, so spricht man von einem MINLP (engl.: mixed-integer nonlinear program).
Gemischt-ganzzahlige lineare Optimierungsprobleme
[Bearbeiten | Quelltext bearbeiten]Einführung
[Bearbeiten | Quelltext bearbeiten]Gemischt-ganzzahlige lineare Optimierungsprobleme (MILP oder nur MIP) sind die wichtigsten Vertreter gemischt-ganzzahliger Optimierungsprobleme, da sich viele große Instanzen global optimal lösen lassen und es zahlreiche Anwendungsmöglichkeiten gibt.[10] Die Bedeutung wird dadurch verstärkt, dass sich viele nichtlineare gemischt-ganzzahlige Probleme linear umformulieren oder zumindest linear approximieren lassen.[1][2] Als jeweils wichtige Spezialfälle enthält die Klasse der gemischt-ganzzahligen linearen Optimierungsprobleme (MILP) die Klasse der kontinuierlichen linearen Optimierungsprobleme (LP) sowie die Klasse der ganzzahligen linearen Optimierungsprobleme (ILP).
Mathematische Definition
[Bearbeiten | Quelltext bearbeiten]Die mathematische Definition eins MILPs erfolgt nun sowohl in Summenschreibweise als auch in einer Matrix-Vektor-Formulierung, da sich die Summenschreibweise in der Regel an gängigen Modellierungsframeworks orientiert, die Matrix-Vektor-Schreibweise jedoch eine kompaktere Formulierung erlaubt.
Definition in Summen-Schreibweise
[Bearbeiten | Quelltext bearbeiten]Jedes MILP lässt sich in Summen-Schreibweise in folgender Form darstellen:
Dabei wurden die Entscheidungsvariablen wie üblich mit , , bezeichnet und alle sonstigen Parameter bezeichnen feste reelle Zahlen.
Definition in Matrix-Vektor-Schreibweise
[Bearbeiten | Quelltext bearbeiten]In Matrix-Vektor-Schreibweise gestaltet sich die Darstellung etwas übersichtlicher.
Hierbei wurden die unteren und oberen Schranken und in entsprechenden Vektoren und untergebracht und alle sonstigen Einträge ebenfalls in Vektoren und Matrizen passender Dimension verstaut.
Beispiel
[Bearbeiten | Quelltext bearbeiten]Das folgende Optimierungsproblem ist ein einfaches Beispiel für ein MILP.
Der eindeutige Optimalpunkt ist , da zunächst die wertvollere ganzzahlige Entscheidungsvariable höchstmöglich gewählt wird und anschließend mit der kontinuierlichen Variablen „aufgefüllt“ wird. Der Optimalwert lautet .
Theoretische Aspekte sowie Grundidee der Lösungsmethoden
[Bearbeiten | Quelltext bearbeiten]Lösungsmethoden für MILPs wie das Branch-and-Cut-Verfahren nutzen aus, dass die kontinuierliche Relaxierung des MILPs – also das Optimierungsproblem, welches entsteht, wenn keine Ganzzahligkeit gefordert wird – ein LP ist und somit effizient lösbar ist. Dadurch entsteht zwar in der Regel keine zulässige Lösung des MILPs, aber der Optimalwert lässt sich dadurch im Maximierungsfall nach oben abschätzen. Diese Schranke kann durch das Hinzufügen von Schnittebenen (engl. cutting planes) noch weiter verbessert werden. Gleichzeitig können etwa durch den Einsatz von Heuristiken gute zulässige Punkte berechnet werden, welche im Maximierungsfall in unteren Grenzen an den Optimalwert resultieren. Dadurch lassen sich worst-case Aussagen über die sogenannte MIP Lücke (engl. MIP gap) treffen, wie etwa William Cook und sein Forschungsteam, die eine Rundreise durch 49687 Pubs in UK berechneten und bewiesen, dass keine Tour existieren könne, die auch nur einen Meter kürzer sei.[11]
Optimierungsmethoden, Komplexität und praktische Lösbarkeit
[Bearbeiten | Quelltext bearbeiten]
Gemischt ganzzahlige Optimierungsprobleme werden durch Branch-and-Bound bzw. Branch-and-Cut-Methoden gelöst. Diese Verfahren besitzen eine theoretisch schlechte Worst-Case-Komplexität, können jedoch durch den Einsatz von Presolve-Techniken[13], Heuristiken, Schnittebenen und Parallelisierung deutlich beschleunigt werden.[14] Dies ermöglicht in vielen Fällen eine globale Lösung sehr großer Ausprägungen NP-schwerer Probleme, wie etwa das Lösen einer Instanz des Problem des Handlungsreisenden mit 85900 Stationen.[15] Es existieren zahlreiche professionelle Implementierungen von Branch-and-Cut-Methoden. Erwähnt seien die kommerziellen Implementierungen (in alphabetischer Reihenfolge) CPLEX, Gurobi und FICO XPress sowie die Open-Source-Pakete CBC, GLPK und SCIP. Darüber hinaus ist es natürlich auch möglich, (Meta)Heuristiken zur Bestimmung guter zulässiger Punkte von gemischt-ganzzahligen Optimierungsproblemen heranzuziehen.
Geschichte der gemischt-ganzzahligen Optimierung
[Bearbeiten | Quelltext bearbeiten]
Höhepunkte der Geschichte der gemischt-ganzzahligen Optimierung sind sicher die Erfindung der Branch-and-Bound-Methode von Alisa Land und Alison Doig im Jahre 1960[16] sowie deren erste professionelle kommerzielle Implementierungen Ende der 1980er Jahre.[10] Für weiterführende Informationen sei auf den nachfolgenden Teilartikel sowie die darin enthaltenen Referenzen verwiesen.
Weiterführende Literatur
[Bearbeiten | Quelltext bearbeiten]- J. Kallrath: Gemischt-ganzzahlige Optimierung: Modellierung in der Praxis, 2. Auflage. Springer Spektrum, Berlin, Heidelberg, 2013, ISBN 978-3-658-00689-1
- A. Schrijver: Theory of Linear and Integer Programming. Wiley, 1998, ISBN 0-471-98232-6.
- N. Sudermann-Merx: Einführung in Optimierungsmodelle. Springer Spektrum, Berlin, Heidelberg, 2023, ISBN 978-3-662-67380-5.
- H. P. Williams: Model Building in Mathematical Programming, 5. Auflage. John Wiley & Sons, Hoboken, New Jersey 2020, ISBN 978-1-118-44333-0.
- L. A. Wolsey: Integer Programming. 2. Auflage. John Wiley & Sons, Hoboken, New Jersey 2020, ISBN 978-1-119-60653-6.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ a b Josef Kallrath: Gemischt-ganzzahlige Optimierung: Modellierung in der Praxis (= Lehrbuch). 2. Auflage. Springer Spektrum, Wiesbaden 2013, ISBN 978-3-658-00689-1.
- ↑ a b c Nathan Sudermann-Merx: Einführung in Optimierungsmodelle. Springer Spektrum, Berlin / Heidelberg 2023, ISBN 978-3-662-67380-5, doi:10.1007/978-3-662-67381-2.
- ↑ a b Leena Suhl, Taïb Mellouli: Optimierungssysteme: Modelle, Verfahren, Software, Anwendungen. 3. Auflage. Springer Gabler, Berlin / Heidelberg 2013, ISBN 978-3-642-38936-8.
- ↑ Gurobi: Case Studies. Abgerufen am 20. Dezember 2023 (amerikanisches Englisch).
- ↑ FICO Xpress: Industries. Abgerufen am 20. Dezember 2023.
- ↑ Josef Kallrath, Panos M. Pardalos, Steffen Rebennack, Max Scheidt (Hrsg.): Optimization in the energy industry (= Energy Systems). Springer, Berlin Heidelberg 2010, ISBN 978-3-540-88965-6.
- ↑ Michael Pinedo: Scheduling: theory, algorithms, and systems. Softcover reprint of the hardcover 5th edition 2016 Auflage. Springer, Cham Heidelberg New York Dordrecht London 2018, ISBN 978-3-319-79973-5.
- ↑ Christopher A. Hane, Cynthia Barnhart, Ellis L. Johnson, Roy E. Marsten, George L. Nemhauser, Gabriele Sigismondi: The fleet assignment problem: Solving a large-scale integer program. In: Mathematical Programming. Band 70, Nr. 1-3, Oktober 1995, ISSN 0025-5610, S. 211–232, doi:10.1007/bf01585938.
- ↑ Dimitris Bertsimas, Angela King, Rahul Mazumder: Best subset selection via a modern optimization lens. In: The Annals of Statistics. Band 44, Nr. 2, 1. April 2016, ISSN 0090-5364, doi:10.1214/15-aos1388, arxiv:1507.03133.
- ↑ a b Robert E. Bixby: A brief history of linear and mixed-integer programming computation. In: Optimization Stories. EMS Press, 2012, ISBN 978-3-936609-58-5, S. 107–121 (uni-bielefeld.de [PDF; 177 kB; abgerufen am 19. Dezember 2023]).
- ↑ UK Pubs Traveling Salesman Problem. Abgerufen am 20. Dezember 2023 (englisch).
- ↑ William Cook: Solution of a 15,112-city TSP. Abgerufen am 19. Dezember 2023.
- ↑ Tobias Achterberg, Robert E. Bixby, Zonghao Gu, Edward Rothberg, Dieter Weninger: Presolve Reductions in Mixed Integer Programming. In: INFORMS Journal on Computing. Band 32, Nr. 2, April 2020, ISSN 1091-9856, S. 473–506, doi:10.1287/ijoc.2018.0857.
- ↑ Mixed-Integer Programming (MIP) – A Primer on the Basics. In: Gurobi Optimization. Abgerufen am 19. Dezember 2023 (amerikanisches Englisch).
- ↑ William Cook: Optimal 85,900-Point Tour. In: https://www.math.uwaterloo.ca/. Abgerufen am 19. Dezember 2023.
- ↑ A. H. Land, A. G. Doig: An Automatic Method of Solving Discrete Programming Problems. In: Econometrica. Band 28, Nr. 3, 1960, ISSN 0012-9682, S. 497, doi:10.2307/1910129.
















![{\displaystyle M\ =\ \{x\in [0,10]:\ |x-5|\geq 2\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6303605cccf1a1e13c43537bfb2dcbc70cfa3235)
![{\displaystyle M\ =\ \{x\in [0,10]:\ x\leq 3{\text{ oder }}x\geq 7\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d649cad4295796afb6038235787ee65865bb84)






![{\displaystyle x\in [7,10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfdd400a7aad60593482d75b72ebccb610135932)


![{\displaystyle x\in [0,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0dc6c3730c66e8211a6ad1aeb36a0dbf0900ef6)
















