Fünfzehneck

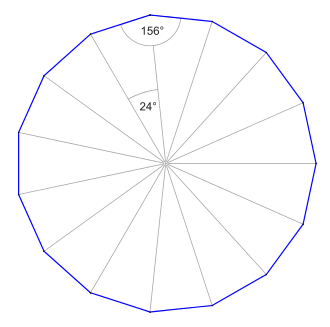
Regelmäßiges Fünfzehneck

Das Fünfzehneck oder Pentadekagon (von altgriechisch πεντεκαίδεκα pentekaídeka, deutsch ‚fünfzehn‘ und γωνία gōnía, deutsch ‚Winkel, Ecke‘) ist eine geometrische Figur und ein Vieleck (Polygon). Es ist bestimmt durch fünfzehn Eckpunkte und deren fünfzehn Verbindungen namens Strecken, Seiten oder Kanten.

Variationen

Das Fünfzehneck ist darstellbar als:

• konkaves Fünfzehneck, in dem mindestens ein Innenwinkel größer als 180° ist. Ein Fünfzehneck kann höchstens sieben solche Winkel haben.
• konvexes Fünfzehneck, in dem alle Innenwinkel kleiner als 180° sind. Ein konvexes Fünfzehneck kann regelmäßig oder unregelmäßig sein.
• Sehnenfünfzehneck, in dem alle Ecken auf einem gemeinsamen Umkreis liegen, aber die Seitenlängen möglicherweise ungleich sind.
• regelmäßiges Fünfzehneck: Es ist bestimmt durch fünfzehn Punkte auf einem virtuellen oder realen Kreis. Die benachbarten Punkte haben zueinander stets den gleichen Abstand und sind mittels aneinandergereihten Strecken, auch Seiten oder Kanten genannt, verbunden.
• regelmäßiges überschlagenes Fünfzehneck: Es ergibt sich, wenn beim Verbinden der fünfzehn Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen $\left\{n/k\right\}$, wobei $n$ die Anzahl der Eckpunkte angibt und jeder $k$-te Punkt verbunden wird.

Es gibt nur drei regelmäßige Fünfzehnstrahlsterne.

Die „Sterne“ mit den Symbolen {15/3} und {15/12} sind regelmäßige Fünfecke, {15/5} und {15/10} gleichseitige Dreiecke und {15/6} und {15/9} regelmäßige Pentagramme.

• Regelmäßige Fünfzehnstrahlsterne
• 
  $\left\{15/2\right\}{,}\ \left\{15/13\right\}$
• 
  $\left\{15/4\right\}{,}\ \left\{15/11\right\}$
• 
  $\left\{15/7\right\}{,}\ \left\{15/8\right\}$

Regelmäßiges Fünfzehneck

Das regelmäßige Fünfzehneck ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel ein konstruierbares Polygon, da die Anzahl seiner Seiten als Produkt paarweise voneinander verschiedener Fermatscher Primzahlen ($15=3\cdot 5$) darstellbar ist. Wie beim regelmäßigen Fünfeck ist der Goldene Schnitt der maßgebende Baustein für eine Konstruktion mit Zirkel und Lineal.

Größen

Größen eines regelmäßigen Fünfzehnecks
Innenwinkel	${\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {13}{15}}\cdot 180^{\circ }\\&=156^{\circ }\end{aligned}}$
Zentriwinkel (Mittelpunktswinkel)	${\begin{aligned}\mu &={\frac {360^{\circ }}{15}}\\\mu &=24^{\circ }\end{aligned}}$
Seitenlänge	${\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{15}}\right)=2\cdot R\cdot \sin(12^{\circ })\\&={\frac {1}{4}}\cdot R\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\approx 0{,}416\cdot R\end{aligned}}$
Umkreisradius	${\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{15}}\right)}}={\frac {a}{2\cdot \sin(12^{\circ })}}\\&={\frac {1}{2}}\cdot a\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)\approx 2{,}405\cdot a\end{aligned}}$
Inkreisradius	${\begin{aligned}r&=a\cdot {\frac {1}{2}}\cdot \cot \left({\frac {180^{\circ }}{15}}\right)=a\cdot {\frac {1}{2}}\cdot \cot(12^{\circ })\\&={\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\approx 2{,}352\cdot a\end{aligned}}$
Höhe	${\begin{aligned}h&=r+R\approx 4{,}757\cdot a\end{aligned}}$
Flächeninhalt	${\begin{aligned}A&={\frac {15}{4}}\cdot a^{2}\cdot \cot \left({\frac {180^{\circ }}{15}}\right)={\frac {15}{4}}\cdot a^{2}\cdot \cot(12^{\circ })\\&={\frac {15}{8}}\cdot a^{2}\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\approx 17{,}642\cdot a^{2}\end{aligned}}$

Mathematische Zusammenhänge

Innenwinkel

Die allgemeine Formel für Polygone liefert:

$\alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {15-2}{15}}\cdot 180^{\circ }={\frac {13}{15}}\cdot 180^{\circ }=156^{\circ }$

Dieser Wert lässt sich auch durch folgende Überlegungen herleiten:

Das Fünfzehneck lässt sich in fünfzehn Dreiecke teilen, deren Seiten jeweils eine Seite des Fünfzehnecks $a$ und die Verbindungsstrecken seines Mittelpunktes mit den zwei Endpunkten der Seite sind. Die Winkel am Mittelpunkt des Fünfzehnecks addieren sich zu $360^{\circ }{\text{,}}$ sein Zentriwinkel beträgt also $24^{\circ }{\text{.}}$ Da die Winkelsumme in einem Dreieck immer $180^{\circ }$ beträgt und das Dreieck gleichschenklig und damit symmetrisch zur Halbierenden des Zentriwinkels ist, schließen die beiden unbekannten Winkel jeweils ${\frac {180^{\circ }-24^{\circ }}{2}}=78^{\circ }$ ein. Da das für alle fünfzehn Dreiecke gilt, addieren sich die beiden Winkel an einem Eckpunkt zu $156^{\circ }$.

Zentriwinkel

Der Zentriwinkel oder Mittelpunktswinkel $\mu$ wird von zwei benachbarten Umkreisradien $R$ eingeschlossen. In der allgemeinen Formel ist für die Variable $n$ die Zahl $15$ einzusetzen.

$\mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{15}}=24^{\circ }$

Seitenlänge und Umkreisradius

Wieder wird das Fünfzehneck in 15 kongruente Dreiecke zerlegt. Nimmt man die Hälfte eines solchen Dreiecks, also ein rechtwinkliges Dreieck mit den Seiten ${\frac {a}{2}}$, $R$ und $r$ sowie mit dem halben Zentriwinkel ${\frac {24^{\circ }}{2}}=12^{\circ },$ so gilt

$\sin(12^{\circ })={\frac {\frac {a}{2}}{R}}={\frac {a}{2\cdot R}}.$

Aus dieser Beziehung folgt

$a=2\cdot R\cdot \sin(12^{\circ })\approx 0{,}416\cdot R.$

Löst man nach $R$ auf, so erhält man

$R={\frac {a}{2\cdot \sin(12^{\circ })}}\approx 2{,}405\cdot a.$

Algebraische Ausdrücke für $a$ bzw. $R$ finden sich in den Abschnitten Berechnung der Seitenlänge und Berechnung des Umkreisradius.

Inkreisradius

Auch der Inkreisradius $r$ lässt sich mithilfe eines halbierten Bestimmungsdreiecks ermitteln. Es ergibt sich

$\tan \left(12^{\circ }\right)={\frac {\frac {a}{2}}{r}}={\frac {a}{2\cdot r}}$.

Durch Multiplikation mit $2\cdot r$ erhält man

$2\cdot r\cdot \tan \left(12^{\circ }\right)=a$

und weiter

$r={\frac {a}{2\cdot \tan \left(12^{\circ }\right)}}$

wegen

${\frac {1}{\tan \left(12^{\circ }\right)}}=\cot \left(12^{\circ }\right)$

gilt auch

$r=a\cdot {\frac {1}{2}}\cdot \cot \left(12^{\circ }\right).$

Algebraische Ausdrücke für $\cot \left(12^{\circ }\right)$ bzw. $r$ finden sich im Abschnitt Berechnung des Inkreisradius.

Höhe

Die Höhe h eines regelmäßigen Fünfzehneckes ist die Summe aus In- und Umkreisradius, da die Verlängerung der Höhe eines Teilstückes über den Mittelpunkt des Fünfzehnecks hinaus auf einen Eckpunkt trifft.

$h=R+r={\frac {a}{2\cdot \sin(12^{\circ })}}+{\frac {a}{2\cdot \tan(12^{\circ })}}\approx 4{,}757\cdot a$

Flächeninhalt

Der Flächeninhalt eines Dreiecks berechnet sich zu $A_{\Delta }={\frac {1}{2}}\cdot a\cdot h_{a}$. Für eines der 15 Bestimmungsdreiecke ist die Höhe $h_{a}$ gleich dem Inkreisradius $r$. Der Flächeninhalt des gesamten Fünfzehnecks beträgt also

$A={\frac {15}{2}}\cdot a\cdot r.$

Zusammen mit dem in Berechnung des Inkreisradius hergeleiteten Ausdruck für $r$ folgt daraus

$A={\frac {15}{2}}\cdot a\cdot {\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)={\frac {15}{8}}\cdot a^{2}\cdot \left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\approx 17{,}642\cdot a^{2}$

Konstruktion mit Zirkel und Lineal bei gegebenem Umkreis

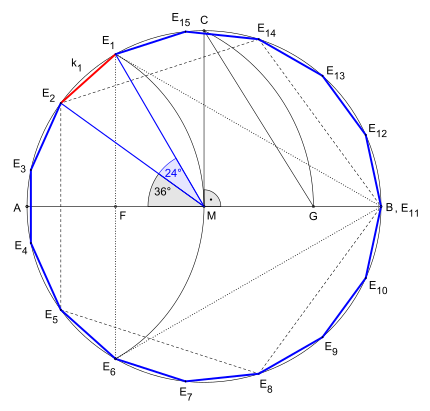
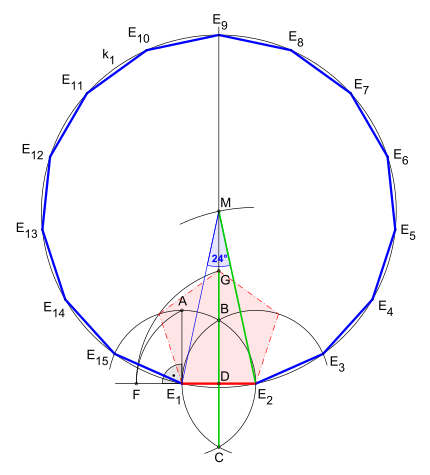
In der hier dargestellten Konstruktion werden ein gleichseitiges Dreieck $BE_{1}E_{6}$ (Schritte 1–3) und die ersten vier Punkte eines regelmäßigen Fünfecks $BE_{14}E_{2}E_{5}E_{8}$ (Schritte 4–6) in den gegebenen Umkreis eingepasst. ${\overline {E_{1}E_{2}}}$ ist dann die Seite eines regelmäßigen Fünfzehnecks im gegebenen Umkreis. Diese Art der Konstruktion beschrieb schon Euklid in seinem Werk Elemente (Die Stoicheia) im IV Buch; die Konstruktionsdetails des Dreiecks und Fünfecks weichen jedoch von seiner Konstruktion ab. Das Bestimmen der ersten Seite des Fünfzehnecks entspricht der Darstellung von Johannes Kepler.

${\overline {AB}}$ bezeichnet die Strecke zwischen den Punkten $A$ und $B{\text{.}}$

Konstruktionsskizze

Animation der Skizze

Ist ein Kreis $k_{1}$ (der Umkreis um das entstehende Fünfzehneck) um den Mittelpunkt $M$ gegeben, lässt sich ein regelmäßiges Fünfzehneck konstruieren durch:

1. Zeichnen eines Durchmessers; Schnittpunkte mit $k_{1}$ sind $A$ und $B$
2. Konstruktion eines Radius, der orthogonal zu ${\overline {AB}}$ steht; Schnittpunkt mit $k_{1}$ ist $C$
3. Konstruktion eines Kreisbogens um $A$ mit dem Radius ${\overline {AM}}$; Schnittpunkte mit $k_{1}$ sind $E_{1}$ und $E_{6}$
4. Zeichnen von ${\overline {E_{1}E_{6}}}$; Schnittpunkt mit ${\overline {AB}}$ ist $F$
5. Zeichnen eines Kreisbogens um $F$ mit dem Radius ${\overline {FC}}$; Schnittpunkt mit ${\overline {AB}}$ ist $G$
6. viermaliges Abtragen der Strecke ${\overline {CG}}$ auf $k_{1}$ ab $B$ entgegen dem Uhrzeigersinn; Schnittpunkte mit $k_{1}$ sind $E_{14}$, $E_{2}$, $E_{5}$, und $E_{8}$; die Verbindung der Eckpunkte $E_{1}$ mit $E_{2}$ ergibt die erste Seite des entstehenden Fünfzehnecks
7. achtmaliges Abtragen der Sehne ${\overline {E_{1}E_{2}}}$ von $k_{1}$ auf $k_{1}$ ab $E_{2}$ entgegen dem Uhrzeigersinn; die Schnittpunkte mit $k_{1}$ sind die restlichen Eckpunkte $E_{3}$, $E_{4}$, $E_{7}$, $E_{9}$, $E_{10}$, $E_{12}$, $E_{13}$ und $E_{15}$ des Fünfzehnecks
8. Verbinden der so gefundenen Punkte.

Berechnung der Seitenlänge

Die in obiger Tabelle angegebene Formel $a={\frac {1}{4}}\cdot R\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)$ für die Seitenlänge leitet sich wie folgt her:

${\mathsf {(1)}}$ Gleichseitiges Dreieck $AME_{1}$

${\mathsf {(1.1)}}\;{\overline {ME_{1}}}=R$ (Umkreisradius)

${\mathsf {(1.2)}}\;{\overline {AM}}={\overline {ME_{1}}}={\overline {AE_{1}}}=R$ nach Konstruktion, Schritt 3

${\mathsf {(1.3)}}\;{\overline {FM}}={\frac {1}{2}}\cdot R$

${\mathsf {(2)}}$ Rechtwinkliges Dreieck $\;FME_{1}$

Es gilt nach dem Satz des Pythagoras: ${\overline {ME_{1}}}^{2}={\overline {FM}}^{2}+{\overline {FE_{1}}}^{2}$

${\begin{aligned}(2.1)\;{\overline {FE_{1}}}&={\sqrt {{\overline {ME_{1}}}^{2}-{\overline {FM}}^{2}}}={\sqrt {R^{2}-\left({\frac {1}{2}}\cdot R\right)^{2}}}={\sqrt {R^{2}-{\frac {1}{4}}\cdot R^{2}}}\\&={\sqrt {{\frac {3}{4}}\cdot R^{2}}}=R\cdot {\sqrt {\frac {3}{4}}}=R\cdot {\frac {\sqrt {3}}{2}}\end{aligned}}$

${\mathsf {(3)}}$ Rechtwinkliges Dreieck $FMC$

Es gilt nach dem Satz des Pythagoras: ${\overline {FC}}^{2}={\overline {FM}}^{2}+{\overline {MC}}^{2}$

${\mathsf {(3.1)}}\;{\overline {FC}}={\sqrt {{{\overline {FM}}^{2}}+{{\overline {MC}}^{2}}}}={\sqrt {\left({\frac {1}{2}}\cdot R\right)^{2}+R^{2}}}={\sqrt {{\frac {5}{4}}\cdot R^{2}}}=R\cdot {\frac {\sqrt {5}}{2}}$

${\mathsf {(3.2)}}\;{\overline {FG}}={\overline {FC}}=R\cdot {\frac {\sqrt {5}}{2}}\;$ nach Konstruktion, Schritt 5

${\mathsf {(4)}}$ Rechtwinkliges Dreieck $ABE_{2}$

$\angle ABE_{2}$ bezeichnet den von ${\overline {AB}}$ und ${\overline {BE_{2}}}$ eingeschlossenen Winkel $\beta$:

${\mathsf {(4.1)}}\;{\overline {MG}}={\overline {FG}}-{\overline {FM}}=R\cdot {\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\cdot R=R\cdot {\frac {{\sqrt {5}}-1}{2}}$

${\mathsf {(4.2)}}\;{\overline {AE_{2}}}={\overline {MG}}=R\cdot {\frac {{\sqrt {5}}-1}{2}}\;$

Nach dem Satz des Thales ist das Dreieck $ABE_{2}$ rechtwinklig, wieder gilt nach dem Satz des Pythagoras: ${\overline {AB}}^{2}={\overline {AE_{2}}}^{2}+{\overline {BE_{2}}}^{2}$

${\begin{aligned}{\mathsf {(4.3)}}\;{\overline {BE_{2}}}&={\sqrt {{\overline {AB}}^{2}-{\overline {AE_{2}}}^{2}}}={\sqrt {{(2\cdot R)}^{2}-\left({R\cdot {\frac {{\sqrt {5}}-1}{2}}}\right)^{2}}}={\sqrt {4\cdot R^{2}-{R^{2}}\cdot {\frac {\left({\sqrt {5}}-1\right)^{2}}{4}}}}\\&=R\cdot {\sqrt {4-{\frac {\left({\sqrt {5}}-1\right)^{2}}{4}}}}=R\cdot {\sqrt {{\frac {16}{4}}-{\frac {\left(5-2\cdot {\sqrt {5}}+1\right)}{4}}}}=R\cdot {\sqrt {\frac {10+2\cdot {\sqrt {5}}}{4}}}\\&=R\cdot {\sqrt {{\frac {1}{4}}\cdot \left(10+2\cdot {\sqrt {5}}\right)}}=R\cdot {\frac {1}{2}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}\end{aligned}}$

${\begin{aligned}{\mathsf {(4.4)}}\;\sin \left(\beta \right)&={\frac {\overline {AE_{2}}}{\overline {AB}}}={\frac {R\cdot {\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)}{2\cdot R}}={\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)\;=\sin \left(18^{\circ }\right)\\&\Rightarrow \angle \;ABE_{2}=\beta =18^{\circ }\end{aligned}}$

${\begin{aligned}{\mathsf {(4.5)}}\;\cos \left(\beta \right)&={\frac {\overline {BE_{2}}}{\overline {AB}}}={\frac {R\cdot {\frac {1}{2}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}}{2\cdot R}}={\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}\;=\cos \left(18^{\circ }\right)\end{aligned}}$

${\mathsf {(5)}}$ Gleichschenkliges Dreieck $E_{1}E_{2}M$

${\mathsf {(5.1)}}\;{\overline {E_{1}E_{2}}}=a$ (Seitenlänge)

${\mathsf {(5.2)}}\;\angle {HME_{2}}={\frac {1}{2}}\cdot \mu =12^{\circ }$

${\mathsf {(5.3)}}\sin \left(18^{\circ }\right)={\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)$ aus (4.4)

${\mathsf {(5.4)}}\cos \left(18^{\circ }\right)={\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}$ aus (4.5)

Zur Berechnung der Seitenlänge benötigt man den Wert von $\sin(12^{\circ })$, der sich mithilfe der Additionstheoreme berechnen lässt:

${\begin{aligned}{\mathsf {(6)}}\;\sin(12^{\circ })&=\sin(30^{\circ }-18^{\circ })\\&=\sin(30^{\circ })\cdot \cos \left(18^{\circ }\right)-\cos \left(30^{\circ }\right)\cdot \sin \left(18^{\circ }\right)\\&={\frac {1}{2}}\cdot {\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}-{\frac {1}{2}}\cdot {\sqrt {3}}\cdot {\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)\\&={\frac {1}{8}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\end{aligned}}$

Damit ergibt sich für die Seitenlänge:

${\begin{aligned}{\mathsf {(7)}}\;a&=2\cdot R\cdot \sin \left(12^{\circ }\right)\\&=2\cdot R\cdot {\frac {1}{8}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\\&={\frac {1}{4}}\cdot R\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\end{aligned}}$

Berechnung des Inkreisradius

Die in obiger Tabelle angegebene Formel $r={\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)$ für den Inkreisradius leitet sich wie folgt her:

${\mathsf {(1)}}$ Rechtwinkliges Dreieck $MHE_{2}$

${\mathsf {(1.1)}}\;{\overline {MH}}=r=a\cdot {\frac {1}{2}}\cdot \cot \left(12^{\circ }\right)$ aus Mathematische Zusammenhänge, Inkreisradius

${\mathsf {(1.2)}}\;\angle {HME_{2}}={\frac {1}{2}}\cdot \mu =12^{\circ }$

${\mathsf {(1.3)}}\sin \left(12^{\circ }\right)={\frac {1}{8}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)$ aus Berechnung der Seitenlänge (6.1)

Zur Berechnung des Inkreisradius benötigt man für den Term $\cot(12^{\circ })={\frac {\cos(12^{\circ })}{\sin(12^{\circ })}}$ zuerst den Wert von $\cos(12^{\circ }),$ der sich mithilfe der Additionstheoreme berechnen lässt:

${\begin{aligned}{\mathsf {(2)}}\;\cos(12^{\circ })&=\cos(30^{\circ }-18^{\circ })\\&=\cos(30^{\circ })\cdot \cos \left(18^{\circ }\right)+\sin \left(30^{\circ }\right)\cdot \sin \left(18^{\circ }\right)\\&={\frac {1}{2}}\cdot {\sqrt {3}}\cdot {\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}+{\frac {1}{2}}\cdot {\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)\\&={\frac {1}{8}}\cdot \left({\sqrt {3}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}\right)\right)+{\frac {1}{8}}\cdot \left({\sqrt {5}}-1\right)\\&={\frac {1}{8}}\cdot \left({\sqrt {30+6{\sqrt {5}}}}+{\sqrt {5}}-1\right)\end{aligned}}$

Die folgende hergeleitete Beziehung lässt sich zur Umformung von Rechenausdrücken verwenden.

${\begin{aligned}{\mathsf {(3)}}\;{\sqrt {10+2{\sqrt {5}}}}&=({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}\end{aligned}}$   denn es gilt

${\begin{aligned}{\mathsf {(3.1)}}\;({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}&={\sqrt {({\sqrt {5}}-1)^{2}\,(5+2{\sqrt {5}})}}\\&={\sqrt {(5-2{\sqrt {5}}+1)\,(5+2{\sqrt {5}})}}\\&={\sqrt {(6-2{\sqrt {5}})\,(5+2{\sqrt {5}})}}\\&={\sqrt {30+12{\sqrt {5}}-10{\sqrt {5}}-20}}\\&={\sqrt {10+2{\sqrt {5}}}}\end{aligned}}$

${\begin{aligned}{\mathsf {(4)}}\;\sin \left(12^{\circ }\right)&={\frac {1}{8}}\,\left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\qquad {\mbox{(aus (1.3))}}\\&={\frac {1}{8}}\,\left(({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}\,({\sqrt {5}}-1)\right)\qquad {\mbox{(nach (3))}}\\&={\frac {1}{8}}\,({\sqrt {5}}-1)\left({\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}\right)\\\end{aligned}}$

${\begin{aligned}{\mathsf {(5)}}\;\cos \left(12^{\circ }\right)&={\frac {1}{8}}\,\left({\sqrt {30+6{\sqrt {5}}}}+{\sqrt {5}}-1\right)\qquad {\mbox{(aus (2))}}\\&={\frac {1}{8}}\,\left({\sqrt {3}}\,{\sqrt {10+2{\sqrt {5}}}}+{\sqrt {5}}-1\right)\\&={\frac {1}{8}}\,\left({\sqrt {3}}\,({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}+({\sqrt {5}}-1)\right)\qquad {\mbox{(nach (3))}}\\&={\frac {1}{8}}\,({\sqrt {5}}-1)\,\left({\sqrt {3}}\,{\sqrt {5+2{\sqrt {5}}}}+1\right)\\\end{aligned}}$

Zur abschließenden Berechnung des Inkreisradius wird nun der Wert von $\cot \left(12^{\circ }\right)$ ermittelt.

${\begin{aligned}{\mathsf {(6)}}\;\cot \left(12^{\circ }\right)&={\frac {\cos \left(12^{\circ }\right)}{\sin \left(12^{\circ }\right)}}\\&={\frac {{\frac {1}{8}}\,({\sqrt {5}}-1)\,\left({\sqrt {15+6{\sqrt {5}}}}+1\right)}{{\frac {1}{8}}\,({\sqrt {5}}-1)\,\left({\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}\right)}}\\&={\frac {{\sqrt {15+6{\sqrt {5}}}}+1}{{\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}}}\\\end{aligned}}$

• Aus Gründen der besseren Übersicht sind acht dazwischenliegende Berechnungsschritte nur im Bearbeitungsmodus sichtbar!

$\;{\begin{aligned}\cot \left(12^{\circ }\right)&={\frac {2{\sqrt {15}}+2{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}\,({\sqrt {5}}-1)}{4}}\\&={\frac {{\sqrt {15}}+{\sqrt {3}}+{\sqrt {10+2{\sqrt {5}}}}}{2}}\qquad {\mbox{(nach (3))}}\\&={\frac {1}{2}}\left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\end{aligned}}$

Damit ergibt sich für den Inkreisradius $r$

${\begin{aligned}{\mathsf {(7)}}\;r&=a\cdot {\frac {1}{2}}\cdot \cot \left(12^{\circ }\right)\\&=a\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\\&={\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\\\end{aligned}}$

Konstruktion mit Zirkel und Lineal bei gegebener Seitenlänge

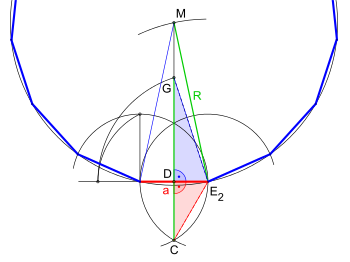
Die Konstruktion ist nahezu gleich mit der des Fünfecks bei gegebener Seitenlänge, auch darin gelingt die Darstellung mittels Verlängerung der Seite und einer damit generierten Strecke, hier ${\overline {FE_{2}}}{\text{,}}$ die nach dem Goldenen Schnitt, äußere Teilung geteilt ist.

${\overline {E_{1}E_{2}}}$ bezeichnet die Strecke zwischen den Punkten $E_{1}$ und $E_{2}{\text{.}}$

Konstruktionsskizze

Animation der Skizze

Ist eine Seite eines Fünfzehnecks gegeben, lässt sich ein regelmäßiges Fünfzehneck konstruieren durch:

1. Bezeichnen der Streckenenden mit $E_{1}$ und $E_{2}$; beide sind Eckpunkte des entstehenden Fünfzehnecks
2. Verlängern der Strecke ${\overline {E_{1}E_{2}}}$ ab $E_{1}$ um ca. einer Länge dieser Strecke
3. Zeichnen eines Kreisbogens um $E_{1}$ mit dem Radius ${\overline {E_{1}E_{2}}}$
4. Konstruktion einer Senkrechten zur Strecke ${\overline {E_{1}E_{2}}}$ ab $E_{1}$; Schnittpunkt mit dem Kreisbogen um $E_{1}$ ist $A$
5. Zeichnen eines Kreisbogens um $E_{2}$ mit dem Radius ${\overline {E_{1}E_{2}}}$; Schnittpunkte mit Kreisbogen um $E_{1}$ sind $B$ und $C$
6. Zeichnen einer geraden Linie ab $C$ durch $B$ (Mittelsenkrechte von ${\overline {E_{1}E_{2}}}$), die etwas mehr als dreimal so lang wie ${\overline {BC}}$ ist; Schnittpunkt mit ${\overline {E_{1}E_{2}}}$ ist $D$
7. Zeichnen eines Kreisbogens um $D$ mit dem Radius ${\overline {DA}}$; Schnittpunkt mit Verlängerung der Strecke ${\overline {E_{1}E_{2}}}$ ist $F$
8. Zeichnen eines Kreisbogens um $E_{2}$ mit dem Radius ${\overline {E_{2}F}}$; Schnittpunkt mit der geraden Linie (ab $C$ durch $B$) ist $G$
9. Zeichnen eines kurzen Kreisbogens um $E_{2}$ mit dem Radius ${\overline {CG}}$; Schnittpunkt mit Verlängerung der Strecke ${\overline {CB}}$ ist $M$, der Mittelpunkt des Umkreises des entstehenden Fünfzehnecks
10. Zeichnen des Umkreises $k_{1}$ um $M$ mit dem Radius ${\overline {ME_{2}}}$; Schnittpunkt mit dem Kreisbogen um $E_{2}$ ist Eckpunkt $E_{3}$
11. elfmaliges Abtragen der Sehne ${\overline {E_{1}E_{2}}}$ von $k_{1}$ auf $k_{1}$; Schnittpunkte mit $k_{1}$ sind die Eckpunkte $E_{3,\dotsc ,15}$ des Fünfzehnecks
12. Verbinden der so gefundenen Eckpunkte.

Berechnung des Umkreisradius

Die in obiger Tabelle angegebene Formel $R=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)$ für den Umkreisradius leitet sich wie folgt her:

${\mathsf {(1)}}\;{\overline {E_{1}E_{2}}}={\overline {E_{1}A}}={\overline {CE_{2}}}=a$ (Seitenlänge)

${\mathsf {(2)}}\;{\overline {DE_{1}}}={\overline {DE_{2}}}={\frac {1}{2}}\cdot a$

${\mathsf {(3)}}$ Rechtwinkliges Dreieck $AE_{1}D$

Es gilt nach dem Satz des Pythagoras: ${\overline {DA}}^{2}={\overline {E_{1}A}}^{2}+{\overline {DE_{1}}}^{2}$

${\mathsf {(3.1)}}\;{\overline {DA}}={\sqrt {{{\overline {E_{1}A}}^{2}}+{{\overline {DE_{1}}}^{2}}}}={\sqrt {a^{2}+\left({\frac {1}{2}}\right)^{2}\cdot a^{2}}}=a\cdot {\sqrt {1+{\frac {1}{4}}}}=a\cdot {\frac {\sqrt {5}}{2}}$

${\mathsf {(3.2)}}\;{\overline {DF}}={\overline {DA}}=a\cdot {\frac {\sqrt {5}}{2}}$ nach Konstruktion, Schritt 7

${\mathsf {(4)}}\;{\overline {E_{1}F}}={\overline {DF}}-{\overline {DE_{1}}}=a\cdot {\frac {\sqrt {5}}{2}}-a\cdot {\frac {1}{2}}=a\cdot \left({\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\right)=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)$

${\begin{aligned}{\mathsf {(5)}}\;{\overline {E_{2}F}}&=a+{\overline {E_{1}F}}=a+a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)=a\cdot \left(1+{\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)\right)\\&=a\cdot \left(1+{\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\right)=a\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)\end{aligned}}$

${\mathsf {(5.1)}}\;{\overline {E_{2}G}}={\overline {E_{2}F}}=a\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)$ nach Konstruktion, Schritt 8

${\mathsf {(6)}}$ Rechtwinkliges Dreieck $DE_{2}G$

Es gilt nach dem Satz des Pythagoras: ${\overline {E_{2}G}}^{2}={\overline {DE_{2}}}^{2}+{\overline {DG}}^{2}$

${\begin{aligned}(6.1)\;{\overline {DG}}\;&={\sqrt {{{\overline {E_{2}G}}^{2}}-{{\overline {DE_{2}}}^{2}}}}={\sqrt {a^{2}\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)^{2}-a^{2}\cdot \left({\frac {1}{2}}\right)^{2}}}=a\cdot {\sqrt {\left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)^{2}-\left({\frac {1}{2}}\right)^{2}}}\\&=a\cdot {\sqrt {{\frac {1}{4}}+{\frac {\sqrt {5}}{2}}+{\frac {5}{4}}-{\frac {1}{4}}}}=a\cdot {\sqrt {{\frac {5}{4}}+{\frac {2\cdot {\sqrt {5}}}{4}}}}=a\cdot {\sqrt {{\frac {1}{4}}\cdot \left(5+2\cdot {\sqrt {5}}\right)}}=a\cdot {\frac {1}{2}}\cdot {\sqrt {5+2\cdot {\sqrt {5}}}}\end{aligned}}$

${\mathsf {(7)}}$ Rechtwinkliges Dreieck ${DCE_{2}}$

Es gilt nach dem Satz des Pythagoras: ${\overline {CE_{2}}}^{2}={\overline {DE_{2}}}^{2}+{\overline {DC}}^{2}$

$(7.1)\;{\overline {DC}}={\sqrt {{\overline {CE_{2}}}^{2}-{\overline {DE_{2}}}^{2}}}={\sqrt {a^{2}-a^{2}\cdot \left({\frac {1}{2}}\right)^{2}}}=a\cdot {\sqrt {\left(1-{\frac {1}{4}}\right)}}=a\cdot {\sqrt {\frac {3}{4}}}=a\cdot {\frac {\sqrt {3}}{2}}$

Nach Konstruktion, Schritt 9 gilt für den Umkreisradius $R:$

${\begin{aligned}(8)\;R&={\overline {E_{2}M}}={\overline {CG}}\\&={\overline {DG}}+{\overline {DC}}=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}\right)+a\cdot {\frac {\sqrt {3}}{2}}\\&=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)\approx 2{,}405\cdot a\end{aligned}}$

Der Goldene Schnitt im Fünfzehneck

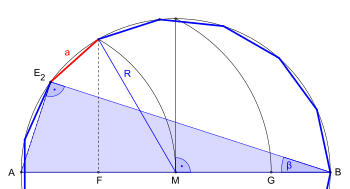
Sowohl in der Konstruktion bei gegebenem Umkreis als auch in der bei gegebener Seitenlänge wird der Goldene Schnitt zur Bestimmung von Konstruktionselementen verwendet.

Teil der Konstruktionsskizze bei gegebenem Umkreis

Teil der Konstruktionsskizze bei gegebener Seitenlänge

• In der Konstruktion bei gegebenem Umkreis teilt der Punkt $M$ die Strecke ${\overline {AG}}$ im Verhältnis des Goldenen Schnittes:

${\frac {\overline {AM}}{\overline {MG}}}={\frac {\overline {AG}}{\overline {AM}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1{,}618{\text{.}}$

• In der Konstruktion bei gegebener Seitenlänge wird die Seite derart verlängert, dass sie die längere Strecke des Verhältnisses ist:

${\frac {\overline {E_{1}E_{2}}}{\overline {E_{1}F}}}={\frac {\overline {E_{2}F}}{\overline {E_{1}E_{2}}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1{,}618{\text{.}}$

Siehe auch

• Sehnenvieleck
• Regelmäßiges Polygon

Literatur

• H. Maser: Die Teilung des Kreises ..., Artikel 365., in Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik, Verlag von Julius Springer, Berlin 1889; Göttinger Digitalisierungszentrum, Universität Göttingen; abgerufen am 15. März 2018.

Weblinks

• Eric W. Weisstein: Pentadecagon. In: MathWorld (englisch). abgerufen am 4. Oktober 2015.