Regressionsanalyse

Die Regressionsanalyse ist ein Instrumentarium statistischer Analyseverfahren, die zum Ziel haben, Beziehungen zwischen einer abhängigen (auch erklärte Variable, Kriterium[svariable], vorhergesagte Variable, Antwortvariable oder Regressand genannt) und einer oder mehreren unabhängigen Variablen (auch erklärende Variable, Prädiktor[variable], Kontrollvariable oder Regressor) zu modellieren. Regressionen werden verwendet, um Zusammenhänge quantitativ zu beschreiben oder Werte der abhängigen Variablen zu prognostizieren. Die häufigste Form der Regressionsanalyse ist die lineare Regression, bei der der Anwender eine Gerade (oder eine komplexere lineare Funktion) findet, die den Daten nach einem bestimmten mathematischen Kriterium am besten entspricht. Beispielsweise berechnet die gewöhnliche Methode der kleinsten Quadrate eine eindeutige Gerade (oder Hyperebene), die die Summe der Abweichungsquadrate zwischen den wahren Daten und dieser Linie (oder Hyperebene), d. h. die Residuenquadratsumme minimiert. Aus bestimmten mathematischen Gründen kann der Anwender den bedingten Erwartungswert der abhängigen Variablen schätzen, wenn die unabhängigen Variablen eine bestimmte Menge von Werten annehmen. Weniger gebräuchliche Formen der Regression verwenden geringfügig unterschiedliche Verfahren zum Schätzen alternativer Lageparameter (z. B. die Quantilsregression) oder zum Schätzen des bedingten Erwartungswertes für eine breitere Klasse nichtlinearer Modelle (z. B. nichtparametrische Regression).

Die Regressionsanalyse wird hauptsächlich zu zwei konzeptionell unterschiedlichen Zwecken verwendet. Erstens wird die Regressionsanalyse häufig für Schätzungen und Vorhersagen verwendet, bei denen sich ihre Verwendung erheblich mit dem Bereich des maschinellen Lernens überschneidet, siehe auch symbolische Regression. Zweitens kann in einigen Situationen eine Regressionsanalyse verwendet werden, um auf kausale Beziehungen zwischen den unabhängigen und abhängigen Variablen zu schließen. Wichtig ist, dass Regressionen für sich genommen nur Beziehungen zwischen einer abhängigen Variablen und einer oder mehrerer unabhängiger Variablen in einem gegebenen Datensatz aufzeigen. Um Regressionen für Vorhersagen zu verwenden oder Kausalzusammenhänge herzuleiten, muss der Anwender sorgfältig begründen, warum bestehende Beziehungen Vorhersagekraft für einen neuen Kontext haben oder warum eine Beziehung zwischen zwei Variablen eine Kausalzusammenhangsinterpretation hat (Korrelation und Kausalzusammenhang). Letzteres ist besonders wichtig, wenn Anwender mithilfe von Beobachtungsdaten kausale Zusammenhänge abschätzen möchten.

Durch die Ergänzung einer Entscheidungsregel wird eine Regression zu einem Klassifikationsverfahren.

Geschichte

Francis Galton

Carl Friedrich Gauß

Die früheste Form der Regression war die Median-Regression (auch Methode der kleinsten absoluten Abweichungen), die um 1760 von Rugjer Josip Bošković vorgeschlagen wurde. Später wurde die Methode der kleinsten Quadrate (französisch méthode des moindres carrés) 1805 von Legendre und 1809 von Gauß veröffentlicht. Beide verwendeten die Methode, um die Umlaufbahnen der Planeten um die Sonne anhand von astronomischen Beobachtungen zu bestimmen. Gauß veröffentlichte eine Weiterentwicklung der Theorie der kleinsten Quadrate im Jahr 1821, die eine theoretische Rechtfertigung seiner Methode der kleinsten Quadrate enthielt. Diese ist heute als Satz von Gauß-Markow bekannt.

Der Begriff Regression wurde im 19. Jahrhundert von Francis Galton, einem Cousin Charles Darwins, geprägt. Er beschrieb damit ein biologisches Phänomen, bekannt als Regression zur Mitte, wonach Nachfahren großer Eltern dazu tendieren, nur durchschnittlich groß zu werden. Für Galton hatte Regression nur diese biologische Bedeutung. Seine Arbeit wurde jedoch später durch Udny Yule und Karl Pearson in einen allgemeineren statistischen Kontext gesetzt. In deren Arbeiten wurde davon ausgegangen, dass die gemeinsame Verteilung der unabhängigen und der abhängigen Variablen normalverteilt ist. Diese Annahme konnte von R. A. Fisher später abgeschwächt werden. Dieser arbeitete mit der Voraussetzung, dass die bedingte Verteilung der abhängigen Variable normalverteilt ist, die gemeinsame Verteilung jedoch nicht notwendigerweise. In dieser Hinsicht war Fishers Ansatz ähnlicher zu Gauß’ Formulierung von 1821.

Regressionsverfahren sind weiterhin ein aktives Forschungsgebiet. In den letzten Jahrzehnten wurden in verschiedensten Bereichen Schätzmethoden entwickelt, etwa zur robusten Regression, zur nichtparametrischen Regression, im Bereich der bayesschen Statistik, bei fehlenden Daten und bei fehlerbehafteten unabhängigen Variablen.

Anwendungen

Regressionsverfahren haben viele praktische Anwendungen. Die meisten Anwendungen fallen in folgende Kategorien:

• Vorhersage: Schätzungen der einzelnen Regressionsparameter $\beta _{0},\beta _{1},\dotsc ,\beta _{k}$ sind weniger wichtig für die Vorhersage, als der Gesamteinfluss der $x$-Variablen auf die Zielgröße $y$. Dennoch sollten gute Schätzer eine hohe Vorhersagekraft haben.
• Datenbeschreibung und Erklärung: Der Statistiker verwendet das geschätzte Modell, um die beobachteten Daten zusammenzufassen und zu beschreiben.
• Parameterschätzung: Die Werte der geschätzten Parameter ${\hat {\beta }}_{0},{\hat {\beta }}_{1},\dotsc ,{\hat {\beta }}_{k}$ könnten theoretische Implikationen für das angenommene Modell haben.
• Variablenauswahl: Es soll herausgefunden werden wie wichtig jede einzelne Prädiktorvariable $x_{j}$ in der Modellierung der Zielgröße $y$ ist. Die Prädiktorvariablen, von denen angenommen wird, dass sie einen wichtigen Anteil an der Erklärung der Variation in $y$ leisten, werden beibehalten und diejenigen, die wenig zur Erklärung der Variation in $y$ beitragen (oder redundante Information über $y$ enthalten), werden ausgelassen.
• Für die Ausgangsvariable kontrollieren: Es wird ein Ursache-Wirkung-Zusammenhang (d. h. ein kausaler Zusammenhang) zwischen der Zielvariable und den Prädiktorvariablen angenommen. Das geschätzte Modell kann dann verwendet werden, um für die Ausgangsvariable eines Prozesses zu kontrollieren, indem die Eingangsvariablen variiert werden. Durch systematisches Herumexperimentieren kann es möglich sein den optimalen Ausstoß zu erzielen.

Schema einer Regressionsanalyse

Datenaufbereitung

Am Beginn jedes statistischen Verfahrens steht die Aufbereitung der Daten, insbesondere

• die Plausibilisierung. Hierbei wird geprüft, ob die Daten nachvollziehbar sind. Dies kann manuell oder automatisch anhand von Gültigkeitsregeln erfolgen.
• der Umgang mit fehlenden Daten. Häufig werden unvollständige Datensätze weggelassen, mitunter werden die fehlenden Daten auch nach bestimmten Verfahren aufgefüllt.
• die Transformation der Daten. Diese kann aus verschiedenen Gründen erfolgen. Sie kann beispielsweise zu einer besseren Interpretierbarkeit oder Visualisierbarkeit der Daten führen. Sie kann auch dazu dienen, die Daten in eine Form zu bringen, in der die Annahmen des Regressionsverfahrens erfüllt sind. Im Falle der linearen Regression werden etwa ein linearer Zusammenhang zwischen den unabhängigen und der abhängigen Variable sowie Homoskedastizität vorausgesetzt. Es gibt mathematische Hilfsmittel zum Finden einer geeigneten Transformation, im Beispiel der Linearisierung des Zusammenhanges etwa die Box-Cox-Transformation.
• die Berücksichtigung von Interaktionen (bei linearer Regression). Hierbei wird neben dem Einfluss der unabhängigen Variablen auch der Einfluss mehrerer Variablen gleichzeitig berücksichtigt.

Modellanpassung

In der Praxis wählt der Anwender zuerst ein Modell aus, das er schätzen möchte, und verwendet dann die gewählte Schätzmethode (z. B. die gewöhnliche Kleinste-Quadrate-Schätzung), um die Parameter dieses Modells zu schätzen. Regressionsmodelle umfassen im Allgemeinen die folgenden Komponenten:

• die unabhängigen Variablen, für die Daten vorliegen und oft im Vektor $\mathbf {x} _{i}$ zusammengefasst werden $\mathbf {x} _{i}^{\top }=(x_{i0},x_{i1},\dotsc ,x_{ik})$ (hierbei stellt $i$ eine Datenreihe dar).
• die abhängige Variable, für die Daten vorliegen und die häufig mit dem Skalar $y_{i}$ angegeben wird. Man sagt: „Variable $y_{i}$ wird auf Variable $x_{i0},x_{i1},\dotsc$ und $x_{ik}$ regressiert“ oder „Regression von $y_{i}$ auf $x_{i0},x_{i1},\dotsc$ und $x_{ik}$“.
• die unbekannten zu schätzenden Parameter $\beta _{0},\beta _{1},\dotsc ,\beta _{k}$: Sie stellen Skalare dar.
• die unbeobachtbaren Störgrößen (statistisches Rauschen), die nicht direkt beobachtet werden können und häufig als $\varepsilon _{i}$ angegeben werden.

In verschiedenen Anwendungsbereichen der Statistik werden unterschiedliche Terminologien anstelle von abhängige und unabhängige Variablen verwendet (siehe Abhängige und unabhängige Variable#Statistische Bezeichnungen und Konzepte).

In den allermeisten Regressionsmodellen ist $Y_{i}$ eine Funktion von $X_{i}$ und $\beta$, wobei diese Beziehung von einer additiven Störgröße $\varepsilon _{i}$ überlagert wird, die für nicht modellierte oder unbekannte Bestimmungsfaktoren von $Y_{i}$ stehen kann:

$Y_{i}=f(X_{i},\beta )+\varepsilon _{i}$.

Ziel des Anwenders ist es, diejenige Funktion $f(X_{i},\beta )$ zu schätzen, die am ehesten zu den vorliegenden Daten passt. Um eine Regressionsanalyse durchzuführen, muss die funktionale Form der Funktion $f(\cdot )$ angegeben werden. Manchmal basiert die Angabe der Form dieser Funktion auf nicht datenbasierten Erfahrungswissen über die Beziehung zwischen $Y_{i}$ und $X_{i}$ (die Lineare Regression etwa betrachtet nur lineare Funktionen $f$, logistische Regression betrachtet nur logistische Funktionen). Wenn kein solches Wissen vorhanden ist, kann eine flexiblere bzw. allgemeinere Form für $f(\cdot )$ gewählt werden. Beispielsweise kann eine einfache lineare Regression (lineare Einfachregression) $f(X_{i},\beta )=\beta _{0}+\beta _{1}X_{i}$ angewandt werden, was darauf hindeutet, dass der Forscher glaubt, dass $Y_{i}=\beta _{0}+\beta _{1}X_{i}+\varepsilon _{i}$ eine angemessene Annäherung für den wahren datengenerierenden Prozess sein könnte.

Sobald der Anwender sein bevorzugtes statistisches Modell festgelegt hat, bieten verschiedene Formen der Regressionsanalyse Werkzeuge zur Schätzung des Parameters $\beta$. Zum Beispiel findet die Kleinste-Quadrate-Schätzung (einschließlich seiner häufigsten Variante, der gewöhnlichen Kleinste-Quadrate-Schätzung) denjenigen Wert von $\beta$, der die Residuenquadratsumme $\sum (Y_{i}-f(X_{i},\beta ))^{2}$ minimiert. Eine gegebene Regressionsmethode liefert letztendlich eine Schätzung von $\beta$, die für gewöhnlich als ${\hat {\beta }}$ bezeichnet wird, um die Schätzung von dem wahren (unbekannten) Parameterwert $\beta$ zu unterscheiden, der die Daten generiert hat. Mit dieser Schätzung kann der Anwender dann den angepassten Wert bzw. vorhergesagten Wert (englisch fitted value) ${\hat {Y}}_{i}=f(X_{i},{\hat {\beta }})$ zur Vorhersage verwenden oder auch zur Beurteilung, wie genau das Modell die Daten erklären kann. Ob der Anwender grundsätzlich an der Schätzung ${\hat {\beta }}$ oder dem vorhergesagten Wert ${\hat {Y}}_{i}$ interessiert ist, hängt vom Kontext und den Zielen des Anwenders ab. Die gewöhnliche Kleinste-Quadrate-Schätzung wird oft verwendet, da die geschätzte Funktion ${\hat {Y}}_{i}=f(X_{i},{\hat {\beta }})$ eine Schätzung des bedingten Erwartungswertes $\operatorname {E} (Y_{i}\mid X_{i})$ darstellt.

Alternative Varianten (z. B. sogenannte robuste Schätzverfahren, die den Betrag der Abweichungen minimieren, wie die Median-Regression oder die Quantilsregression) sind jedoch nützlich, wenn Anwender andere Funktionen $f(X_{i},\beta )$ z. B. nichtlinearer Modelle modellieren möchte.

Es ist wichtig zu beachten, dass genügend Daten vorhanden sein müssen, um ein Regressionsmodell zu schätzen. Angenommen, ein Anwender hat Zugriff auf $n$ Datenzeilen mit einer abhängigen und zwei unabhängigen Variablen: $(Y_{i},X_{1i},X_{2i})$. Sei weiterhin angenommen, der Anwender möchte ein einfaches lineares Modell über die Kleinste-Quadrate-Schätzung schätzen. Das zu schätzende Modell lautet dann $Y_{i}=\beta _{0}+\beta _{1}X_{1i}+\beta _{2}X_{2i}+\varepsilon _{i}$. Wenn der Anwender nur Zugriff auf $n=2$ Datenpunkte hat, kann er unendlich viele Kombinationen $({\hat {\beta }}_{0},{\hat {\beta }}_{1},{\hat {\beta }}_{2})$ finden, die die Daten gleich gut erklären: Es kann eine beliebige Kombination ausgewählt werden, die ${\hat {Y}}_{i}={\hat {\beta }}_{0}+{\hat {\beta }}_{1}X_{1i}+{\hat {\beta }}_{2}X_{2i}$ erfüllt, die alle zu $\sum _{i}{\hat {e}}_{i}^{2}=\sum _{i}({\hat {Y}}_{i}-({\hat {\beta }}_{0}+{\hat {\beta }}_{1}X_{1i}+{\hat {\beta }}_{2}X_{2i}))^{2}=0$ führen und ist daher eine gültige Lösung, die diejenige, die die Summe der Residuenquadrate (Residuenquadratsumme) minimiert. Um zu verstehen, warum es unendlich viele Möglichkeiten gibt, ist zu beachten, dass das System der $n=2$-Gleichungen für 3 Unbekannte gelöst werden muss, wodurch das System unterbestimmt wird. Alternativ kann man unendlich viele dreidimensionale Ebenen visualisieren, die durch $n=2$ Fixpunkte verlaufen.

Ein allgemeinerer Ansatz ist ein Kleinste-Quadrate-Modell mit $k$ unterschiedlichen Parametern zu schätzen. Dazu müssen $N\geq k$ unterschiedliche Datenpunkte vorliegen. Wenn $N>k$ ist, gibt es im Allgemeinen keinen Satz von Parametern, der perfekt zu den Daten passt. Die Größe $N-k$ erscheint häufig in der Regressionsanalyse und wird im Modell als Anzahl der Freiheitsgrade bezeichnet. Um ein Kleinste-Quadrate-Modell zu schätzen, müssen außerdem die unabhängigen Variablen $(X_{1i},X_{2i},...,X_{ki})$ linear unabhängig sein, d. h. man muss keine der unabhängigen Variablen rekonstruieren können, indem man die verbleibenden unabhängigen Variablen addiert und multipliziert. Diese Bedingung stellt sicher, dass die Produktsummenmatrix $\mathbf {X} ^{\top }\mathbf {X}$ eine invertierbare Matrix ist und daher eine Lösung ${\hat {\beta }}$ existiert.

Modellvalidierung

Ein wichtiger Schritt der Regressionsanalyse ist die Modellvalidierung. Hierbei wird überprüft, ob das Modell eine gute Beschreibung des Zusammenhangs ist. Die Modellvalidierung umfasst die

• Residuenanalyse. Viele Regressionsverfahren treffen Annahmen über die Residuen ${\hat {\varepsilon }}_{i}$ des Modells. So wird z. B. eine bestimmte Verteilung, konstante Varianz oder fehlende Autokorrelation unterstellt. Da die Residuen Ergebnis des Verfahrens sind, kann die Prüfung der Annahmen erst im Nachhinein erfolgen. Typisches Hilfsmittel zur Überprüfung der Verteilung ist das Quantil-Quantil-Diagramm.
• Überanpassung. Dieses Phänomen tritt auf, wenn zu viele unabhängige Variablen im Modell berücksichtigt werden. Ein Verfahren zum Testen auf Überanpassung ist das Kreuzvalidierungsverfahren.
• Untersuchung der Daten auf Ausreißer und einflussreiche Datenpunkte. Hierbei wird überprüft, welche Datensätze nicht zur ermittelten Funktion $f(\cdot )$ passen (Ausreißer) und welche Daten die ermittelte Funktion stark beeinflussen. Für diese Datensätze empfiehlt sich eine gesonderte Untersuchung. Mathematische Hilfsmittel zur Ermittlung von Ausreißern und einflussreichen Punkten sind Cook- und Mahalanobis-Abstand.
• Multikollinearität zwischen den unabhängigen Variablen (bei linearen Modellen). Wenn es einen linearen Zusammenhang zwischen den unabhängigen Variablen $x$ gibt, dann kann das zum einen die numerische Stabilität des Verfahrens beeinträchtigen und zum anderen die Interpretation des Modells bzw. der angepassten Funktion erschweren. Hilfsmittel zum Quantifizieren der Kollinearität sind der Varianzinflationsfaktor und die Korrelationsmatrix.

Vorhersage

Das validierte Modell kann zur Vorhersage von Werten von $y$ bei gegebenen Werten von $x$ herangezogen werden. Häufig wird neben dem prognostizierten Wert von $y$ auch ein Vorhersageintervall angegeben, um so die Unsicherheit der Vorhersage abzuschätzen.

Bei Vorhersagen im Wertebereich der zur Modellanpassung verwendeten Daten spricht man von Interpolation. Vorhersagen außerhalb dieses Datenbereichs nennt man Extrapolation. Vor der Durchführung von Extrapolationen sollte man sich gründlich mit den dabei implizierten Annahmen auseinandersetzen.

Variablenauswahl und Modellvergleich

Ist das Ziel der Analyse die Ermittlung derjenigen unabhängigen Variablen, die besonders stark in Zusammenhang mit der abhängigen Variablen $y$ stehen, werden häufig mehrere Modelle mit jeweils unterschiedlichen unabhängigen Variablen erstellt und diese Modelle verglichen. Um zwei Modelle miteinander zu vergleichen, werden in der Regel Kennzahlen wie das Bestimmtheitsmaß oder Informationskriterien benutzt.

Es gibt automatisierte Verfahren wie die sogenannte schrittweise Regression, die sukzessive dasjenige Modell zu ermitteln versuchen, welches den gesuchten Zusammenhang am besten erklärt. Die Anwendung solcher Verfahren wird jedoch kontrovers diskutiert.

Des Weiteren gibt es in der bayesschen Statistik Verfahren, die aus mehreren Modellen ein neues Modell ableiten (durch sogenanntes averaging) und so versuchen, die aus der Modellwahl entstehende Unsicherheit zu verringern.

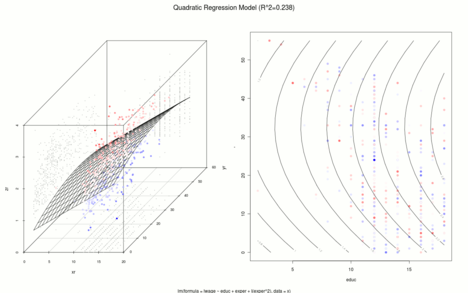
Einige Regressionsverfahren

Das folgende Beispiel wird zur Illustration der verschiedenen Verfahren benutzt. Analog zu Mincer (1974) wurden aus dem Current Population Survey 1985 zufällig 534 Beobachtungen mit folgenden Variablen gezogen:

• ${\text{lwage}}$: natürlicher Logarithmus des Stundenlohns,
• ${\text{educ}}$: Berufsausbildung in Jahren,
• ${\text{exper}}$: Berufserfahrung in Jahren (= Alter – Berufsausbildung – 6).

Mincer untersuchte mit Hilfe der nach ihm benannten Mincer-Einkommensgleichung den Zusammenhang zwischen dem Logarithmus des Stundenlohns (abhängige Variable) und der Berufsausbildung und -erfahrung (unabhängige Variablen). In den folgenden Grafiken findet sich links eine räumliche Darstellung der Regressionsfläche und rechts ein Kontourplot. Positive Residuen sind rötlich, negative Residuen sind bläulich gezeichnet und je heller die Beobachtung desto kleiner ist der Absolutbetrag des Residuums.

• Lineare Regressionen
• 
  ${\text{lwage}}=b_{0}+b_{1}{\text{educ}}+b_{2}{\text{exper}}$.
• 
  ${\text{lwage}}=b_{0}+b_{1}{\text{educ}}+b_{2}{\text{exper}}+b_{3}{\text{exper}}^{2}$.

Grundlegende Verfahren

Lineare Regression

→ Hauptartikel: Lineare Regression

Bei der linearen Regression wird das Modell so spezifiziert, dass die abhängige Variable $y$ eine Linearkombination der Parameter (Regressionsparameter) $\beta _{j}$ ist, aber nicht notwendigerweise der unabhängigen Variablen $x$. Zum Beispiel modelliert die einfache lineare Regression die Abhängigkeit mit einer unabhängigen Variable $x$:

$y_{i}=\beta _{0}+\beta _{1}x_{i}+\varepsilon _{i}\quad i=1,\dotsc ,n$.

Bei der multiplen linearen Regression werden mehrere unabhängige Variablen oder Funktionen der unabhängigen Variablen berücksichtigt. Wird zum Beispiel der Term $(x_{i2})^{2}$ zur vorigen Regression hinzugefügt, so ergibt sich:

$y_{i}=\beta _{0}+\beta _{1}x_{i1}+\beta _{2}(x_{i2})^{2}+\varepsilon _{i}\quad i=1,\dotsc ,n$.

Obwohl der Ausdruck auf der rechten Seite quadratisch in der unabhängigen Variable $x_{i2}$ ist, ist der Ausdruck linear in den Parametern $\beta _{0}$, $\beta _{1}$ und $\beta _{2}$. Damit ist dies auch eine lineare Regressionsgleichung.

Zur Bestimmung der Modellparameter $\beta _{j}$ wird die Methode der kleinsten Quadrate verwendet.

Nichtparametrische Regression

Bei nichtparametrischen Regressionsverfahren wird die Form des funktionalen Zusammenhangs f nicht vorgegeben, sondern weitestgehend aus den Daten hergeleitet. Bei der Schätzung der unbekannten Regressionsfunktion $m(\cdot )$ an der Stelle $(x_{1},\dotsc ,x_{k})$ gehen die Daten nahe diesem Punkt mit größerem Gewicht ein als Datenpunkte, die weit entfernt von diesem liegen.

Zur Schätzung haben sich verschiedene Regressionsverfahren etabliert:

Nadaraya-Watson-Schätzer

• Kernregression:

Hierbei wird die Regressionsfunktion als gewichtete Summe der naheliegende Beobachtungswerte berechnet. Die Gewichte werden mittels Kerndichteschätzung bestimmt und dann eine

• lokal konstante lineare Regression (Nadaraya-Watson-Schätzer),
• lokal lineare Regression (lokal linearer Schätzer) oder
• lokal polynomiale Regression (lokal polynomialer Schätzer)

durchgeführt.

• Multivariate adaptive Regressionssplines

Bei der Methode der multivariaten adaptiven Regressions-Splines (MARS) wird die abhängige Variable als Linearkombination von sogenannten Hockeystick-Funktionen (bzw. Produkten von Hockeystickfunktionen) dargestellt.

Semiparametrische Regression

Ein Nachteil der nichtparametrischen Regressionen ist, dass sie am Fluch der Dimensionalität leiden. D. h. je mehr erklärende Variablen es gibt, desto mehr Beobachtungen sind notwendig, um an einem beliebigen Punkt $(x_{1},\dotsc ,x_{k})$ die unbekannte Regressionsfunktion $m(x_{1},\dotsc ,x_{k})$ zuverlässig zu schätzen. Daher wurde eine Reihe von semi-parametrischen Modellen etabliert, die die lineare Regression erweitern bzw. nutzen:

• Additive Modelle

Hier wird die unbekannte Regressionsfunktion als Summe nichtparameterischer linearer Einfachregressionen $g_{j}$ der Variablen dargestellt:

$m(x_{1},\dotsc ,x_{k})=b_{0}+b_{1}g_{1}(x_{1})+\dotsb +b_{k}g_{k}(x_{k})$

Beim partiell linearen Modell geht ein Teil der Variablen linear ein, insbesondere binäre Variablen.

• Additive Modelle
• 
  ${\text{lwage}}=b_{0}+g_{1}({\text{educ}})+g_{2}({\text{exper}})$
• 
  ${\text{lwage}}=b_{0}+b_{1}{\text{educ}}+g_{2}({\text{exper}})$

• Index-Modelle

Hier wird die unbekannte Regressionsfunktion ebenfalls als Summe nichtparameterischer linearer Einfachregressionen $g_{j}$ von Indices dargestellt:

$m(x_{1},\dotsc ,x_{k})=g_{1}\left(b_{0}^{(1)}+b_{1}^{(1)}x_{1}+\dotsb +b_{k}^{(1)}x_{k}\right)+\dotsb +g_{M}\left(b_{0}^{(M)}+b_{1}^{(M)}x_{1}+\dotsb +b_{k}^{(M)}x_{k}\right)$

Im Fall $M=1$ spricht man vom Single-Index-Modell; für $M>1$ gibt es die Projection-Pursuit-Regression.

• Index-Modelle
• 
  ${\text{lwage}}=g_{1}(b_{0}^{(1)}+b_{1}^{(1)}{\text{educ}}+b_{2}^{(1)}{\text{exper}})$
• 
  ${\begin{aligned}\ {\text{lwage}}&\ =g_{1}(b_{0}^{(1)}+b_{1}^{(1)}{\text{educ}}+b_{2}^{(1)}{\text{exper}})\\&\ +g_{2}(b_{0}^{(2)}+b_{1}^{(2)}{\text{educ}}+b_{2}^{(2)}{\text{exper}})\end{aligned}}$

Robuste Regression

→ Hauptartikel: Robuste Schätzverfahren

Regressionsverfahren, die auf der Kleinste-Quadrate-Schätzung oder der Maximum-Likelihood-Schätzung beruhen, sind nicht robust gegenüber Ausreißern. Robuste Regressionsverfahren wurden entwickelt, um diese Schwäche der klassischen Methode zu umgehen. So können zum Beispiel alternativ M-Schätzer eingesetzt werden.

Verallgemeinerte Verfahren

Verallgemeinerte lineare Modelle

→ Hauptartikel: Verallgemeinerte lineare Modelle

Bei der klassischen linearen Regression wird vorausgesetzt, dass die Störgrößen $\varepsilon _{i}$ normalverteilt sind. Die Modellannahme wird bei den verallgemeinerten Modellen abgeschwächt, wo die Störgrößen $\varepsilon _{i}$ eine Verteilung aus der Verteilungsklasse der exponentiellen Familie besitzen können. Dies wird möglich durch die Verwendung

• einer bekannten Kopplungsfunktion $g(\cdot )$, abhängig von der Verteilungsklasse der Störgrößen, und
• der Maximum-Likelihood-Methode (Methode der größten Plausibilität) zur Bestimmung der Modellparameter.

Ein Spezialfall der verallgemeinerten linearen Modelle ist die logistische Regression. Wenn die Antwortvariable $Y$ eine kategoriale Variable ist, die nur zwei oder endlich viele Werte annehmen darf, verwendet man häufig die logistische Regression.

Binäre logistische Regression: $g(\mu )=\log \left({\frac {\mu }{1-\mu }}\right)=\beta _{0}+\beta _{1}x_{i1}+\dotsb +\beta _{k}x_{ik}+\varepsilon _{i}$

mit $\mu =P(Y=1\mid X=x)$ (abhängig von Verteilungsklasse der Störgrößen). Eine Alternative wäre das Probit-Modell.

Verallgemeinerte semiparametrische Modelle

Diese Idee ist auch für die semiparametrischen Modelle übernommen worden:

• Verallgemeinerte additive Modelle (englisch generalized additive models, kurz: GAM)
  $g(\mu )=\beta _{0}+f_{1}(x_{1})+\dotsb +f_{k}(x_{k})$.

Eine besondere Art der verallgemeinerten additiven Modelle stellen die sogenannten verallgemeinerten additiven Modelle für Lage-, Skalen- und Formparameter dar.

• Verallgemeinerte partiell lineare Modelle (englisch generalized partial linear models, kurz: GPLM)
  $g(\mu )=\beta _{0}+\beta _{1}z_{1}+\dotsb +\beta _{k}z_{k}+f(x_{1},\dotsc ,x_{q})$.
• Verallgemeinerte additive partiell lineare Modelle (englisch generalized additive partial linear models, kurz: GAPLM)
  $g(\mu )=\beta _{0}+\beta _{1}z_{1}+\dotsb +\beta _{k}z_{k}+f_{1}(x_{1})+\dotsb +f_{q}(x_{q})$.

Tensorregression

→ Hauptartikel: Tensorregression

Bei der Tensorregression werden Regressionsmodelle verwendet, welche Tensoren beinhalten. Solche Modelle sind vor allem bei hochdimensionalen oder großen Daten interessant. Viele klassische Regressionsmodelle, wie die verallgemeinerten linearen Modelle, besitzen auch ein Analogon in der Tensorwelt.

Spezielle Verfahren

Autoregressive Modelle

Wenn die Datenpunkte geordnet sind (z. B. wenn es sich bei den Daten um eine Zeitreihe handelt), dann ist es etwa in autoregressiven Modellen und autoregressiven bedingt heteroskedastischen Modellen möglich, vorhergehende Daten als „unabhängige“ Variable zu verwenden.

Siehe auch

• Regression mit stochastischen Regressoren

Literatur

• Norman R. Draper, Harry Smith: Applied Regression Analysis. Wiley, New York 1998.
• Ludwig Fahrmeir, Thomas Kneib, Stefan Lang: Regression: Modelle, Methoden und Anwendungen. Springer Verlag, Berlin / Heidelberg / New York 2007, ISBN 978-3-540-33932-8.
• Dieter Urban, Jochen Mayerl: Regressionsanalyse: Theorie, Technik und Anwendung. 2., überarb. Auflage. VS Verlag, Wiesbaden 2006, ISBN 3-531-33739-4.
• M.-W. Stoetzer: Regressionsanalyse in der empirischen Wirtschafts- und Sozialforschung – Eine nichtmathematische Einführung mit SPSS und Stata. Berlin 2017, ISBN 978-3-662-53823-4.

Weblinks

Wikibooks: Einführung in die Regressionsrechnung – Lern- und Lehrmaterialien

Wikibooks: ${\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}$: Mathematik für die Schule

• Literatur über Regressionsanalyse im Katalog der Deutschen Nationalbibliothek