Box-Plot
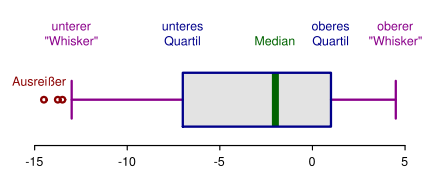
Der Box-Plot (auch Boxplot, Box-Whisker-Plot oder Kastengrafik) ist ein Diagramm, das zur grafischen Darstellung der Verteilung eines mindestens ordinalskalierten Merkmals verwendet wird.[1][2] Es fasst dabei verschiedene robuste Streuungs- und Lagemaße in einer Darstellung zusammen. Ein Box-Plot soll schnell einen Eindruck davon vermitteln, in welchem Bereich die Daten liegen und wie sie sich über diesen Bereich verteilen. Dazu werden alle Werte der sogenannten Fünf-Punkte-Zusammenfassung, also der Median, das untere und obere Quartil sowie der kleinste und größte Wert, dargestellt.
Box-Plots zählen zu den wichtigsten Darstellungsarten der beschreibenden Statistik[3] und haben sich als nützliches Instrument der explorativen Datenanalyse erwiesen.[4]
Aufbau
[Bearbeiten | Quelltext bearbeiten]Ein Box-Plot besteht immer aus einem Rechteck, genannt „Box“, und zwei Linien, die dieses Rechteck verlängern. Diese Linien werden als „Antennen“, seltener als „Fühler“ oder „Whisker“ bezeichnet und durch einen Strich abgeschlossen. Innerhalb der Box verläuft ein durchgehender Strich, der den Median der Verteilung repräsentiert. Box-Plots werden horizontal („liegend“) oder vertikal („stehend“) gezeichnet.
Box
[Bearbeiten | Quelltext bearbeiten]Die Box entspricht dem Bereich, in dem die mittleren 50 % der Daten liegen. Sie wird also durch das obere und das untere Quartil begrenzt, und die Länge der Box entspricht dem Interquartilsabstand (englisch interquartile range, IQR). Ihre Breite wird meist nach ästhetischen Gesichtspunkte gewählt.[5]
Antenne (Whisker)
[Bearbeiten | Quelltext bearbeiten]

Durch die Antennen werden die außerhalb der Box liegenden Werte dargestellt. Im Gegensatz zur Box sind die Antennen nicht einheitlich definiert.
Eine Definition beschränkt die Länge der Antennen auf maximal das 1,5-Fache des Interquartilsabstands (1,5×IQR). Dabei enden die Antennen jedoch nicht genau nach dieser Länge, sondern bei dem Wert aus den Daten, der noch innerhalb dieser Grenze liegt.[6] Die Länge der Antennen werden also durch die Datenwerte und nicht allein durch den Interquartilsabstand bestimmt. Dies ist auch der Grund, warum die Antennen nicht auf beiden Seiten gleich lang sein müssen. Gibt es keine Werte außerhalb der Grenze von 1,5×IQR, werden die Längen der Antennen durch den maximalen und minimalen Wert festgelegt. Andernfalls werden die Werte außerhalb der Antennen separat in das Diagramm eingetragen. Diese Werte können dann als ausreißerverdächtig behandelt werden oder werden direkt als Ausreißer bezeichnet.[7] Ein Box-Plot, dem diese Definition zugrunde liegt, wird in der Literatur auch modifizierter Box-Plot genannt.[7]
Ausreißer, die zwischen 1,5×IQR und 3×IQR liegen, werden auch als „milde Ausreißer“ bezeichnet und Werte, die über 3×IQR liegen, als „extreme Ausreißer“ oder „Extremwerte“. Zur besseren Unterscheidung werden milde und extreme Ausreißer im Box-Plot manchmal mit unterschiedlichen Symbolen gekennzeichnet.
Eine weitere Definition sieht vor, dass die Antennen bis zum größten bzw. kleinsten Wert des Datensatzes reichen. In dieser Darstellung sind keine Ausreißer mehr erkennbar, da die Box inklusive Antennen die gesamte Spannweite der Daten abdeckt. Allgemein lässt sich sagen, dass die Definition der Ausreißer in der Literatur nicht einheitlich ist und deshalb die genaue Definition, welche in einem Box-Plot verwendet wurde, beschrieben werden sollte.
Weitere mögliche Bestandteile
[Bearbeiten | Quelltext bearbeiten]
Manchmal wird auch das arithmetische Mittel in einen Box-Plot mit eingetragen (als Kreuz, Punkt oder Stern).[8]
Im gekerbten (engl. notched) Box-Plot werden auch Konfidenzintervalle für den Median aufgenommen.[9] Dazu wird um die Medianlinie eine „Kerbe“ eingefügt, deren Breite die Länge des 95%-Konfidenzintervalls widerspiegelt. Dadurch lässt sich beurteilen, ob die Unterschiede zwischen den Medianen verschiedener Untergruppen statistisch signifikant sind: Dies ist der Fall, wenn sich die Kerben der Boxplots zweier Untergruppen nicht überlappen.[10]
Zusammenfassung der Kennwerte
[Bearbeiten | Quelltext bearbeiten]Der Vorteil eines Box-Plots besteht darin, dass gewisse Kennwerte einer Verteilung direkt aus der graphischen Darstellung abgelesen werden können.
| Kennwert | Beschreibung | Lage im Box-Plot |
|---|---|---|
| Minimum | Kleinster Wert des Datensatzes | Ende einer Antenne oder entferntester Ausreißer |
| Unteres Quartil | Die kleinsten 25 % der Werte sind kleiner als dieser oder gleich diesem Kennwert | Beginn der Box |
| Median | Die kleinsten 50 % der Werte sind kleiner als dieser oder gleich diesem Kennwert | Strich innerhalb der Box |
| Oberes Quartil | Die kleinsten 75 % der Werte sind kleiner als dieser oder gleich diesem Kennwert | Ende der Box |
| Maximum | Größter Wert des Datensatzes | Ende einer Antenne oder entferntester Ausreißer |
| Spannweite | Differenz zwischen Maximum und Minimum, also Größe des Wertebereiches | Länge des gesamten Box-Plots (inklusive Ausreißer) |
| Interquartilsabstand | Wertebereich, in dem sich die mittleren 50 % der Daten befinden. (Liegt zwischen dem 0,25- und dem 0,75-Quartil.) | Länge der Box |
Anwendung
[Bearbeiten | Quelltext bearbeiten]Aufgrund des einfachen Aufbaus von Box-Plots werden diese hauptsächlich verwendet, um sich schnell einen Überblick über einen Datensatz zu verschaffen. Die Box gibt an, in welchem Bereich die mittleren 50 % der Daten liegen, und die Box inklusive Antennen gibt an, in welchem Bereich der Großteil der Daten bzw. alle Daten liegt. Der Median innerhalb der Box teilt das gesamte Diagramm in zwei Bereiche, in denen jeweils 50 % der Daten liegen. An seiner Lage kann man erkennen, ob eine Verteilung symmetrisch oder schief ist: Ist der Median innerhalb der Box nach links verschoben (bei waagerechter Darstellung), so ist die Verteilung rechtsschief, und umgekehrt.[11] Weniger geeignet ist der Box-Plot für bi- oder multimodale Verteilungen. Um solche Eigenschaften aufzudecken, empfiehlt sich die Verwendung von Histogrammen oder die grafische Umsetzung von Kerndichteschätzungen.
Box-Plots mit Antennen von maximal dem eineinhalbfachen Interquartilsabstand eignen sich auch, um eventuelle Ausreißer zu identifizieren, oder liefern Hinweise darauf, ob die Daten einer bestimmten Verteilung unterliegen. Wenn der Box-Plot stark asymmetrisch ist, eine ungewöhnlich hohe Ausreißerzahl oder weit von der Box entfernte Ausreißer enthält, deutet das beispielsweise darauf hin, dass die Daten nicht normalverteilt sind.
Ein wesentlicher Vorteil des Box-Plot besteht im raschen Vergleich der Verteilung in verschiedenen Untergruppen.[3] Während ein Histogramm eine zweidimensionale Ausdehnung hat, ist ein Box-Plot im Wesentlichen eindimensional, so dass sich leicht mehrere Datensätze nebeneinander (oder untereinander bei waagerechter Darstellung) auf derselben Skala darstellen und vergleichen lassen.
Beispiel
[Bearbeiten | Quelltext bearbeiten]
Dieses Beispiel beruht auf einer Messreihe mit den folgenden 20 Datenpunkten:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| (unsortiert) | 9 | 6 | 7 | 7 | 3 | 9 | 10 | 1 | 8 | 7 | 9 | 9 | 8 | 10 | 5 | 10 | 10 | 9 | 10 | 8 |
| (sortiert) | 1 | 3 | 5 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 10 | 10 | 10 | 10 | 10 |
Ein Box-Plot hilft dabei, schnell einen Überblick über diese Daten zu erhalten. So erkennt man direkt, dass der Median (durchgezogene Linie) genau bei 8,5 liegt und dass je 25 % der Daten unter 7 bzw. über 9,5 liegen, denn dies sind genau die Abmessungen der Box, in der 50 % der Messwerte enthalten sind. Folglich ist auch der Interquartilsabstand, der der Länge der Box entspricht, genau 2,5.
Dieser Box-Plot wurde mit Antennen bis zu einer Länge des 1,5-fachen Interquartilsabstands erstellt. Diese sind also maximal 3,75 Maßeinheiten lang. Allerdings reichen Whisker stets nur bis zu einem Wert aus den Daten, der sich noch innerhalb dieser 3,75 Einheiten befindet. Der obere Whisker verläuft also nur bis zu 10, da es keinen größeren Wert in den Daten gibt, und der untere Whisker nur bis 5, da der nächstkleinere Wert weiter als 3,75 vom Anfang der Box entfernt ist.
Die Werte von 1 und 3 werden im Box-Plot als Ausreißer markiert, da sie sich nicht innerhalb der Box oder der Antennen befinden. Bei diesen Werten sollte untersucht werden, ob es sich tatsächlich um Ausreißer oder um fehlerhaft eingegebene oder anderweitig auffällige Werte handelt.
Da sich der Median innerhalb der Box leicht rechts befindet, kann außerdem auf eine Linksschiefe der zugrundeliegenden Verteilung der Messdaten geschlossen werden. Insbesondere scheint den Daten keine (symmetrische) Normalverteilung zugrunde zu liegen.
Geschichte
[Bearbeiten | Quelltext bearbeiten]Die erste Darstellung eines Box-Plots findet sich unter der Bezeichnung range-bar im Buch Charting Statistics von Mary Eleanor Spears aus dem Jahr 1952. Dort reichen die Antennen bis zu den Extremwerten.[12] Der Begriff Box-Plot geht auf John W. Tukey zurück, der in seinem Buch Exploratory Data Analysis aus dem Jahr 1977 von box-and-whisker plots spricht. Darin schlägt er vor, die Länge der Antennen auf den 1,5-fachen Interquartilsabstand zu begrenzen.
Siehe auch
[Bearbeiten | Quelltext bearbeiten]- Streuungsfächer, kreisförmiges Diagramm, das die gleichen Angaben zur Streuung wie ein Box-Plot darstellt.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Mary Eleanor Spear: Charting Statistics. McGraw-Hill, 1952, S. 164–166. (archive.org)
- John W. Tukey: Exploratory data analysis. Addison-Wesley, 1977, ISBN 0-201-07616-0, S. 27–56.
- Falk et al.: Foundations of statistical analysis and applications with SAS. Birkhäuser, 2002.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Interaktiver Box-Plot
- Ausführliche Erklärung und Beispiele
- Erklärung und kostenlose Excel-Vorlage
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Franz Kronthaler: Statistik angewandt mit dem R Commander – Datenanalyse ist (k)eine Kunst. 2. Auflage. Springer, Berlin / Heidelberg 1991, ISBN 978-3-662-63603-9, Abschn. 4.7 Der Boxplot, S. 54–55, doi:10.1007/978-3-662-63604-6.
- ↑ Karl Mosler, Friedrich Schmid: Beschreibende Statistik und Wirtschaftsstatistik. 4. Auflage. Springer, Berlin / Heidelberg 2009, ISBN 978-3-642-01556-4, S. 33.
- ↑ a b Andreas Büchter, Hans-Wolfgang Henn: Elementare Stochastik. 2. Auflage. Springer, 2007, ISBN 978-3-540-45381-9, S. 93.
- ↑ Reinhold Kosfeld, Hans Friedrich Eckey, Matthias Türck: Deskriptive Statistik. 6. Auflage. Springer Gabler, 2016, ISBN 978-3-658-13639-0, S. 115.
- ↑ Norbert Henze: Stochastik für Einsteiger. 13. Auflage. Springer Spektrum, 2021, ISBN 978-3-662-63839-2, S. 33.
- ↑ John W. Tukey: Exploratory data analysis. 1977, S. 47.
- ↑ a b Marco Burkschat, Erhard Cramer, Udo Kamps: Beschreibende Statistik. 2. Auflage. Springer Spektrum, 2012, ISBN 978-3-642-30012-7, S. 107.
- ↑ Markus Oestreich, Oliver Romberg: Keine Panik vor Statistik. 7. Auflage. Springer Spektrum, 2022, ISBN 978-3-662-64489-8, S. 79.
- ↑ Robert McGill, John W. Tukey, Wayne A. Larsen: Variations of Box Plots. In: The American Statistician. Band 32, Nr. 1, 1978, S. 12–16.
- ↑ James L. Mullenex: Box Plots: Basic and Advanced. In: The Mathematics Teacher. Band 83, Nr. 2, 1990, S. 108–112.
- ↑ Thomas Cleff: Deskritive Statistik und explorative Datenanalyse. 3. Auflage. Springer Gabler, 2015, ISBN 978-3-8349-4747-5, S. 53.
- ↑ Aiman Obed, Armin Goralczyk: Boxplot uneinheitlich. In: Deutsches Ärzteblatt. Band 107, Nr. 7, 2010, S. 122 (aerzteblatt.de).



