Maschinelles Lernen

Typisches Vorgehen beim maschinellen Lernen (ML)

Beispiel für ein statistisches Modell: Die Linie (rot) zeigt ein lineares Modell für einfach strukturierte Beispieldaten (blau). Siehe auch Überwachtes Lernen#Lineare Regression

Maschinelles Lernen (ML) entwickelt, untersucht und verwendet statistische Algorithmen, auch Lernalgorithmen genannt. Lernalgorithmen können Lösungen für Probleme lernen, die zu kompliziert sind, um sie mit Regeln zu beschreiben, zu denen es aber viele Daten gibt, die als Beispiele für die gewünschte Lösung dienen können. Ein Lernalgorithmus bildet vorgegebene Beispieldaten auf ein mathematisches Modell ab. Dabei passt der Lernalgorithmus das Modell so an, dass es von den Beispieldaten auf neue Fälle verallgemeinern kann. Dieser Vorgang wird Training genannt. Nach dem Training ist der gefundene Lösungsweg im Modell gespeichert. Er wird nicht explizit programmiert. Das trainierte Modell kann für neue Daten Vorhersagen treffen oder Empfehlungen und Entscheidungen erzeugen. In der mathematischen Statistik bezeichnet man dieses Fachgebiet auch als statistisches Lernen.

Aus dem weiten Spektrum möglicher Anwendungen seien hier genannt: Spamfilter, automatisierte Diagnose­verfahren, Erkennung von Kreditkartenbetrug, Aktienmarkt­analysen, Klassifikation von Nukleotidsequenzen, Sprach- und Texterkennung.

Allgemein formuliert lernt ein Lernalgorithmus beim Training aus den Beispieldaten eine Funktion, die auch für neue, nicht zuvor gelernte Dateneingaben eine korrekte Ausgabe erzeugt. Es gibt verschiedene Lernstile, die sich darin unterscheiden, woher der Algorithmus beim Training Informationen dazu erhält, was „korrekt“ ist.

Am häufigsten wird das überwachte Lernen eingesetzt. Dabei werden Vorgaben in Form von korrekten Ausgabewerten oder Rückmeldungen zur Verfügung gestellt. Beim unüberwachten Lernen werden keine Vorgaben gemacht. Die Algorithmen durchsuchen die Beispieldaten beispielsweise nach Kriterien für die Einteilung in unterschiedliche Cluster oder nach korrelierenden Merkmalen, die zusammengefasst werden können, um die Daten zu vereinfachen. Da es keine Vorgaben gibt, können diese Algorithmen unterschiedliche Lösungen vorschlagen, die anschließend zu bewerten sind. Beim bestärkenden Lernen beobachten Lernsysteme, die als Agenten bezeichnet werden, eine Umgebung und reagieren auf sie, indem sie Aktionen ausführen. Für die Aktionen erhalten sie Belohnungen. Diese Lernsysteme entwickeln selbständig eine Strategie, um möglichst viele Belohnungen zu erhalten.

Geschichte

Dieser Abschnitt gibt einen kurzen Überblick über wichtige Ereignisse und Meilensteine.

1943 beschreiben Warren McCulloch und Walter Pitts ein Modell für ein künstliches Neuron, das später als McCulloch-Pitts-Zelle bekannt wird. Sie zeigen auch, dass künstliche Neuronen miteinander zu einem Netz verbunden werden können, mit dem sich praktisch jede logische oder arithmetische Funktion berechnen lassen könnte.

1957 publiziert Frank Rosenblatt das Perzeptron-Modell, das aus einer einzelnen Schicht von künstlichen Neuronen besteht.

In den 1960ern werden Algorithmen für Bayessche Netze entwickelt. Bayessche Netze können beispielsweise vorhersagen, mit welcher Wahrscheinlichkeit eine bestimmte Diagnose zu den Daten eines Patienten passt.

1969 weisen Marvin Minsky und Seymour Papert nach, dass man mit Netzen, die nur aus einer Schicht von künstlichen Neuronen bestehen, nicht jede gegebene Funktion berechnen kann, weil man damit keine XOR-Verknüpfung (exklusives Oder) modellieren kann. Für das Training mehrschichtiger Netze ist zu dieser Zeit kein funktionierendes Verfahren bekannt. Danach stagniert die Forschung an künstlichen neuronalen Netzen.

1982 beschreibt Paul Werbos ein Verfahren, das das Training mehrschichtiger Netze erlaubt. Es ist heute als Backpropagation bekannt. Es folgt ein neuer Aufschwung in der Forschung an künstlichen neuronalen Netzen.

In den 1990ern gibt es große Fortschritte durch die Entwicklung von Support Vector Machines (SVMs) und rekurrenten neuronalen Netzen (RNNs). Wissenschaftler beginnen mit der Entwicklung von Programmen, die große Datenmengen analysieren und aus den Ergebnissen Regeln „lernen“.

In den 2000ern wird ML zunehmend auch in der Öffentlichkeit bekannt. Die stetige Zunahme von Rechenleistung und verfügbaren Datenmengen ermöglicht weitere Fortschritte. 2001 veröffentlicht Leo Breiman die Grundlagen für ein als Random Forest bekanntes Verfahren, das eine Gruppe von Entscheidungsbäumen trainiert.

2006 beschreiben Geoffrey Hinton et al. eine Methode, mit der man ein neuronales Netz, das aus mehreren Schichten von künstlichen Neuronen besteht, so trainieren kann, dass es handgeschriebene Zahlen mit einer Genauigkeit von über 98 % erkennen kann. Bis dahin schien es unmöglich zu sein, mit solchen Netzen hohe Genauigkeiten bei der Klassifikation zu erreichen. Die neue Methode wird Deep Learning genannt.

In den folgenden Jahren wird das Deep Learning weiter entwickelt. Es führt zu enormen Fortschritten in der Bild- und Textverarbeitung.

2017 gewinnt AlphaGo im Go-Spiel gegen den besten Spieler der Weltrangliste.

Ebenfalls 2017 stellt ein Forscherteam von Google einen Artikel zur Transformer-Architektur vor. Diese enthält einen Aufmerksamkeitsmechanismus. Netze, die diese Architektur verwenden, lernen beim Training nicht nur, wie sie Daten verarbeiten sollen, sondern auch, auf welchen Teil einer Sequenz sie im vorgegebenen Kontext ihre Aufmerksamkeit richten sollen. Verglichen mit den bis dahin eingesetzten Architekturen reduziert sich dadurch der Aufwand für das Training beispielsweise von Sprachmodellen erheblich.

2020 wird AlphaFold in der medizinischen Fachwelt als Durchbruch in der Proteinstrukturvorhersage aufgenommen. Das Programm ist in der Lage, die 3D-Struktur von Molekülen vorherzusagen.

2022 wird der Chatbot ChatGPT öffentlich zugänglich gemacht. Das Programm ist in der Lage, mit Nutzern über textbasierte Nachrichten und Bilder zu kommunizieren.

2024 wird AlphaFold 3 vorgestellt. Dieses Programm ist in der Lage, sowohl die 3D-Struktur von Molekülen als auch ihre Interaktion untereinander und mit anderen Molekülen vorherzusagen.

Verwandte Fachgebiete

Künstliche Intelligenz

Das maschinelle Lernen ist ein Teilgebiet des Fachgebietes „Künstliche Intelligenz“, auch KI genannt. Das Fachgebiet „Künstliche Intelligenz“ ist ein Teilgebiet der Informatik mit dem Ziel, menschliche Intelligenz zu imitieren. Etwa ab 1980 entwickelten sich die Ziele und Methoden innerhalb des Fachbereiches KI in verschiedene Richtungen. Die meisten Forscher versuchten vorrangig, durch die Verarbeitung von bekanntem Wissen in Expertensystemen menschliche Intelligenz nachzubilden. Gleichzeitig untersuchte eine kleine Gruppe von Forschern, ob sich die Leistung von Computern bei Vorhersagen dadurch verbessern lässt, dass sie Wissen aus Daten lernen, die Informationen zu Erfahrungen aus dem Problemfeld enthalten. Der Bereich KI zeigte zu dieser Zeit nur wenig Interesse am Lernen aus Daten. Deshalb gründeten diese Forscher den neuen Bereich ML. Das Ziel von ML ist nicht mehr, menschliche Intelligenz zu imitieren, sondern praktische Probleme zu lösen. Inzwischen betrachten viele Experten ML als eine Schlüsseltechnologie der KI. Die öffentliche Berichterstattung verwendet die Bezeichnung KI oft gleichbedeutend mit ML.

Statistik

ML und Statistik verwenden sehr ähnliche Methoden. Die beiden Fachgebiete unterscheiden sich allerdings in ihrem Hauptziel. Viele der eingesetzten Methoden können sowohl angewendet werden, um Schlussfolgerungen zu ziehen als auch, um Vorhersagen zu treffen. Die Statistik benutzt Daten von sorgfältig ausgewählten Stichproben, um daraus Rückschlüsse zu Eigenschaften einer zu untersuchenden Gesamtmenge zu ziehen. Die Methoden in der Statistik legen deshalb den Schwerpunkt darauf, statistische Modelle zu erstellen und diese genau an die gegebene Problemstellung anzupassen. Damit kann man berechnen, mit welcher Wahrscheinlichkeit gefundene Zusammenhänge echt sind und nicht durch Störungen erklärt werden können. Dieses Schließen von Daten auf (hypothetische) Modelle wird als statistische Inferenz bezeichnet. Die Methoden im ML hingegen verarbeiten große Datenmengen und lernen daraus mit allgemein formulierten Algorithmen Zusammenhänge, die verallgemeinert und für Vorhersagen benutzt werden. Auch wenn ein maschinell gelerntes Modell für ein gegebenes Problem überzeugende Vorhersageergebnisse liefert, kann es unmöglich sein, die Zusammenhänge zu überprüfen, die das Modell gelernt hat und für seine Vorhersagen verwendet.

Data Science

ML ist ein wichtiger Baustein des interdisziplinären Wissenschaftsfeldes „Data Science“. Dieser Bereich befasst sich mit der Extraktion von Erkenntnissen, Mustern und Schlüssen sowohl aus strukturierten als auch unstrukturierten Daten.

Data-Mining und Knowledge Discovery in Databases

ML ist eng verwandt mit „Data-Mining“. Unter Data-Mining versteht man die systematische Anwendung statistischer Methoden auf große Datenbestände (insbesondere „Big Data“ bzw. Massendaten) mit dem Ziel, neue Querverbindungen und Trends zu erkennen. Viele Algorithmen können für beide Zwecke verwendet werden. Algorithmen aus dem ML werden beim Data-Mining angewendet und Methoden der Knowledge Discovery in Databases können genutzt werden, um Lerndaten für ML zu produzieren oder vorzuverarbeiten.

Mathematische Optimierung

Die mathematische Optimierung ist eine mathematische Grundlage des ML. Die bestmögliche Anpassung eines Modells an die Trainingsdaten ist ein Optimierungsproblem. Beispielsweise wenden einige Lernalgorithmen das Gradientenverfahren an, um Modellparameter zu optimieren. In der Theorie des computergestützten Lernens bietet das Probably Approximately Correct Learning einen Rahmen für die Beschreibung des ML.

Methoden

Die Methoden von ML können nach verschiedenen Kriterien in Kategorien eingeteilt werden.

Repräsentation des Wissens

Das maschinelle Lernen verarbeitet Beispieldaten und leitet daraus Regeln ab. Viele Anwendungsfälle erfordern, dass die Regeln, die das Modell gelernt hat und im Einsatz verwendet, von Menschen nachvollzogen und überprüft werden können.

Symbolische Ansätze

Ursprünglich hatte ML das Ziel, automatisch Expertensysteme zu erzeugen und nachzubilden, wie Menschen lernen. Der Schwerpunkt lag auf symbolischen Ansätzen. Bei symbolischen Ansätzen wird das Wissen in Form von Regeln oder logischen Formeln repräsentiert. Dadurch können Menschen die Zusammenhänge und Muster, die das System für seine Vorhersagen benutzt, leicht erkennen und überprüfen. Dabei werden aussagenlogische und prädikatenlogische Systeme unterschieden. In der Aussagenlogik hat jede Aussage einen von genau zwei Wahrheitswerten. Der Wahrheitswert jeder zusammengesetzten Aussage ist eindeutig durch die Wahrheitswerte ihrer Teilaussagen bestimmt. Ein Beispiel für ein solches System ist ein Entscheidungsbaum. Bekannte Algorithmen dafür sind ID3 und sein Nachfolger C4.5. Die Prädikatenlogik ist eine Erweiterung der Aussagenlogik. Sie spielt in der Konzeption und Programmierung von Expertensystemen eine Rolle, siehe auch induktive logische Programmierung.

Nicht-symbolische Ansätze

Später änderte ML sein Ziel dahingehend, dass alle Methoden untersucht werden sollten, die die Leistung steigern können. Dazu gehören auch nicht-symbolische Ansätze, beispielsweise künstliche neuronale Netze. Diese speichern die gelernten Regeln implizit in den Parametern des Modells. Das bedeutet, dass Menschen nicht einfach erkennen und überprüfen können, welche Zusammenhänge und Muster das System für eine Vorhersage benutzt. Der Aufwand dafür, Entscheidungen nachzuvollziehen, beispielsweise durch Untersuchungen dazu, wie das Modell auf kleine Änderungen der Eingangsdaten reagiert, kann sehr hoch sein.

Training

Beim Training bildet ein Lernalgorithmus vorgegebene Beispieldaten auf ein mathematisches Modell ab. Nach dem Training ist der gefundene Lösungsweg im Modell gespeichert. Er wird nicht explizit programmiert. Das trainierte Modell kann für neue Daten Vorhersagen treffen oder Empfehlungen und Entscheidungen erzeugen.

Beim Training baut der Lernalgorithmus ein Modell auf und passt die Parameter so an, dass die Ergebnisse des Modells die gegebene Aufgabe möglichst gut lösen. Dabei unterscheidet man drei Hauptgruppen der Trainingsüberwachung oder des Lernstils: überwachtes Lernen (englisch supervised learning), unüberwachtes Lernen (englisch unsupervised learning) und bestärkendes Lernen (engl. reinforcement learning).

Überwachtes Lernen

→ Hauptartikel: Überwachtes Lernen

Beim überwachten Lernen wird das Modell mit Datensätzen trainiert und validiert, die für jede Eingabe einen passenden Ausgabewert enthalten. Man bezeichnet solche Datensätze als markiert oder gelabelt. Beim Training passt der Lernalgorithmus Parameter des Modells so an, dass die Ausgaben des Modells möglichst gut mit den bekannten, richtigen Ausgaben übereinstimmen. Die Ausgaben des Modells werden also durch die vorgegebenen Ausgaben „überwacht“. Typische Anwendungsbeispiele sind Klassifikation und Regression.

Der Lernalgorithmus baut zunächst in der Lernphase mit einem Teil der Beispieldaten, dem Trainingsdatensatz, ein statistisches Modell auf. Nach der Lernphase wird die Qualität des erzeugten Modells mit einem anderen Teil der Beispieldaten, dem Testdatensatz, überprüft. Das Ziel ist, dass das Modell auch für völlig neue Daten das geforderte Verhalten zeigt. Dazu muss sich das Modell gut an die Trainingsdaten anpassen, gleichzeitig muss eine Überanpassung vermieden werden.

Es lassen sich noch einige Unterkategorien für überwachtes Lernen identifizieren, die in der Literatur häufiger erwähnt werden:

• Teilüberwachtes Lernen (englisch semi-supervised learning): Der Datensatz enthält nur für einen Teil der Eingaben die dazugehörigen Ausgaben. Nun werden in der Regel zwei Algorithmen kombiniert. Im ersten Schritt teilt ein Algorithmus für unüberwachtes Lernen die Eingaben in Cluster auf und labelt anschließend alle Eingaben eines Clusters mit dem Label anderer Datenpunkte aus demselben Cluster. Danach wird ein Algorithmus für überwachtes Lernen eingesetzt.
• Aktives Lernen (englisch active learning): Der Algorithmus hat die Möglichkeit, für einen Teil der Eingaben die korrekten Ausgaben zu erfragen. Dabei muss der Algorithmus die Fragen bestimmen, welche einen hohen Informationsgewinn versprechen, um die Anzahl der Fragen möglichst klein zu halten.
• Selbstüberwachtes Lernen (englisch self-supervised learning): Diese Methode kann wie das teilüberwachte Lernen in zwei Schritte aufgeteilt werden. Im ersten Schritt erstellt ein Algorithmus aus einem völlig ungelabelten Datensatz einen neuen Datensatz mit Pseudolabeln. Dieser Schritt gehört eigentlich zum unüberwachten Lernen. Danach wird ein Algorithmus für überwachtes Lernen eingesetzt.

Unüberwachtes Lernen

→ Hauptartikel: Unüberwachtes Lernen

Der Algorithmus erzeugt für eine gegebene Menge von Eingaben ein statistisches Modell, das die Eingaben beschreibt und erkannte Kategorien und Zusammenhänge enthält und somit Vorhersagen ermöglicht. Clustering-Verfahren teilen Daten in mehrere Kategorien ein, die sich durch charakteristische Muster voneinander unterscheiden. Diese Verfahren erstellen selbständig Klassifikatoren. Ein wichtiger Algorithmus in diesem Zusammenhang ist der EM-Algorithmus, der iterativ die Parameter eines Modells so festlegt, dass es die gesehenen Daten optimal erklärt. Er legt dabei das Vorhandensein nicht beobachtbarer Kategorien zugrunde und schätzt abwechselnd die Zugehörigkeit der Daten zu einer der Kategorien und die Parameter, die die Kategorien ausmachen. Eine Anwendung des EM-Algorithmus findet sich beispielsweise in den Hidden Markov Models (HMMs). Andere Methoden des unüberwachten Lernens, z. B. die Hauptkomponentenanalyse, zielen darauf ab, die beobachteten Daten in eine einfachere Repräsentation zu übersetzen, die sie trotz drastisch reduzierter Information möglichst genau wiedergibt. Ein typisches Anwendungsbeispiel ist die Vorbereitung von Datensätzen für das überwachte Lernen.

Bestärkendes Lernen

→ Hauptartikel: Bestärkendes Lernen

Beim bestärkenden Lernen beobachten Lernsysteme, die als Agenten bezeichnet werden, eine Umgebung und reagieren auf sie, indem sie Aktionen ausführen. Für die Aktionen erhalten sie Belohnungen. Diese Lernsysteme entwickeln selbständig eine Strategie, um möglichst viele Belohnungen zu erhalten. Aufgrund seiner Allgemeingültigkeit wird dieses Gebiet auch in vielen anderen Disziplinen untersucht, z. B. in der Spieltheorie, der Kontrolltheorie, dem Operations Research, der Informationstheorie, der simulationsbasierten Optimierung, den Multiagentensystemen, der Schwarmintelligenz, der Statistik und den genetischen Algorithmen. Beim maschinellen Lernen wird die Umgebung normalerweise als Markov-Entscheidungsprozess (MDP) dargestellt. Viele Algorithmen des Verstärkungslernens verwenden Techniken der dynamischen Programmierung. Verstärkungslernalgorithmen setzen keine Kenntnis eines exakten mathematischen Modells des MDP voraus. Sie werden eingesetzt, wenn exakte Modelle nicht durchführbar sind. Verstärkungslernalgorithmen werden in autonomen Fahrzeugen oder beim Lernen eines Spiels gegen einen menschlichen Gegner eingesetzt. Ein bekanntes Anwendungsbeispiel ist AlphaGo.

Batch- und Online-Learning

Beim Batch-Learning, auch Offline-Learning genannt, werden alle Beispieldaten auf einmal eingelesen. Das System kann in dieser Zeit nicht benutzt werden und ist in der Regel Offline. Nach dem Training kann das System nicht durch neue Daten verbessert werden. Wenn neue Daten dazu gelernt werden sollen, dann ist ein vollständiger neuer Trainingslauf mit allen alten und neuen Daten erforderlich.

Beim Online-Learning, auch inkrementelles Lernen genannt, wird das System inkrementell mit kleineren Datensätzen trainiert. Das Verfahren eignet sich gut für Systeme, die sich schnell an Veränderungen anpassen müssen. Dabei müssen neue Daten genau so hochwertig sein wie alte. Wenn neue Daten beispielsweise ungeprüft von einem defekten Sensor übernommen werden, besteht die Gefahr, dass das Modell mit der Zeit schlechter wird.

Lernen von Instanzen oder Modellen

Beim ML geht es oft darum, Vorhersagen zu treffen. Dazu muss ein System von den gelernten Daten auf unbekannte Daten verallgemeinern.

Eine einfache Methode besteht darin, dass das System direkt die Merkmale von neuen Datenpunkten mit denen der gelernten Datenpunkte vergleicht und ihre Ähnlichkeit vergleicht. Das bezeichnet man als instanzbasiertes Lernen. In der Trainingsphase lernt das System nur die Trainingsdaten. Danach berechnet es bei jeder Anfrage die Ähnlichkeit von neuen Datenpunkten mit gelernten und erzeugt aus dem Ähnlichkeitsmaß eine Antwort. Ein Beispiel ist die Nächste-Nachbarn-Klassifikation.

Die andere Methode besteht darin, dass das System in der Trainingsphase ein Modell entwickelt und seine Parameter so an die Trainingsdaten anpasst, dass das Modell korrekte Verallgemeinerungen oder Vorhersagen machen kann. Das bezeichnet man als modellbasiertes Lernen.

Daten

Ausschnitt aus dem MNIST-Testdatensatz. Mit diesem Datensatz kann man beispielsweise ein Convolutional Neural Network so trainieren, dass es handgeschriebene Ziffern erkennen kann.

Das Erstellen von Datensätzen mit geeigneten Beispieldaten kann mit einem hohen Aufwand verbunden sein. Die Abbildung zum MNIST-Datensatz zeigt als Beispiel einen kleinen Ausschnitt von Beispieldaten, mit denen ML das komplizierte Problem der automatischen Erkennung von handgeschriebenen Ziffern sehr gut lösen kann.

Die Beispieldaten müssen in maschinenlesbarer Form vorliegen und Informationen über Beobachtungen oder Erfahrungen enthalten, die für das Lösen des Problems relevant und repräsentativ sind. Eine Lösung für das gegebene Problem kann nur dann korrekt gelernt werden, wenn die Beispieldaten alle relevanten Merkmale korrekt, vollständig und ohne Stichprobenverzerrungen erfassen.

Die Daten dürfen nur diejenigen Muster aufweisen, die das Modell zur Entscheidung heranziehen soll. Andere Muster müssen entfernt werden. Beispielsweise wurde schon beobachtet, dass ein künstliches neuronales Netz, das darauf trainiert werden sollte, Züge auf Bildern zu erkennen, tatsächlich nur auf Gleise achtete. Der Aufwand dafür, solche Fehler zu erkennen und die Ursachen zu beheben, kann sehr hoch sein.

Die meisten maschinellen Lernverfahren benötigen eine große Zahl von Beispieldaten, um ein statistisches Modell zu erzeugen, das die zu lernende Funktion hinreichend genau abbildet. Bei komplizierten Problemen lässt sich die Genauigkeit eher durch größere Datensätze als durch bessere Lernalgorithmen verbessern.

Modelle

Während des Trainings erzeugt ein Lernalgorithmus ein mathematisches Modell der Trainingsdaten und passt die Modellparameter an die Trainingsdaten an. Nach dem Training kann das so erzeugte Modell neue Daten verarbeiten, um Vorhersagen zu treffen. Generative Modelle können nach dem Training auch neue Daten erzeugen, die den gelernten Daten ähneln, beispielsweise neue Texte, Bilder oder Videos.

Es gibt viele Arten von Modellen, die untersucht wurden und in solchen Systemen verwendet werden. Im Folgenden werden einige Modelle, die oft eingesetzt werden, kurz beschrieben.

Lineare Regression

→ Hauptartikel: Lineare Regression

Einfache lineare Regression auf einem Datensatz

Die lineare Regression ist ein statistisches Verfahren, mit dem versucht wird, eine beobachtete abhängige Variable durch eine oder mehrere unabhängige Variablen zu erklären. Bei der linearen Regression wird dabei ein lineares Modell angenommen. Bei der einfachen linearen Regression wird mithilfe zweier Parameter eine Gerade (Regressionsgerade) so durch eine Punktwolke gelegt, dass der lineare Zusammenhang zwischen $X$ und $Y$ möglichst gut beschrieben wird.

Um eine möglichst genaue Vorhersage für die abhängige Variable zu erhalten, wird eine Kostenfunktion aufgestellt. Diese Funktion beschreibt die mittlere quadratische Abweichung, die dadurch entsteht, dass die Regressionsgerade die zu erklärende Variable nur approximiert und nicht genau darstellt. Der Lernalgorithmus minimiert die Kostenfunktion.

Logistische Regression

→ Hauptartikel: Logistische Regression

Beispiel einer logistischen Regression. Die Kurve zeigt die geschätzte Wahrscheinlichkeit dafür, ein Examen zu bestehen (ja/nein), in Abhängigkeit von der Lernzeit.

Die logistische Regression ist eine oft eingesetzte Methode zum Lösen von binären Klassifikationsproblemen. Sie schätzt zunächst, mit welcher Wahrscheinlichkeit ein gegebener Datenpunkt zu einer bestimmten Klasse gehört. Danach entscheidet sie, ob die berechnete Wahrscheinlichkeit größer ist als 50 %. In diesem Fall gibt sie diese Klasse als Ergebnis aus. Andernfalls gibt sie die andere Klasse als Ergebnis aus.

Während man bei der linearen Regression die mittlere quadratische Abweichung minimiert, um die optimalen Werte für die Parameter zu erhalten, maximiert man bei der logistischen Regression die Likelihood-Funktion, um die optimalen Werte der Parameter zu erhalten. Dieses Verfahren wird als Maximum-Likelihood-Methode bezeichnet.

k-Means-Algorithmus

→ Hauptartikel: k-Means-Algorithmus

Die Objekte werden dem Cluster zugewiesen, dessen Zentrum am nächsten ist.

Der k-Means-Algorithmus ist ein Verfahren zur Vektorquantisierung, das auch zur Clusteranalyse verwendet wird. Dabei wird aus einer Menge von ähnlichen Objekten eine vorher bekannte Anzahl von k Gruppen gebildet. Der Algorithmus ist eine der am häufigsten verwendeten Techniken zur Gruppierung von Objekten, da er schnell die Zentren der Cluster findet. Dabei bevorzugt der Algorithmus Gruppen mit geringer Varianz und ähnlicher Größe.

In der Regel wird ein approximativer Algorithmus verwendet, der mit zufälligen Mittelwerten aus dem Trainingsdatensatz beginnt und sich danach in mehreren Schritten einer guten Clusteraufteilung annähert. Da die Problemstellung von k abhängig ist, muss dieser Parameter vom Benutzer festgelegt werden.

Support Vector Machines

→ Hauptartikel: Support Vector Machine

Zwei mögliche Trenngeraden mit verschiedenen Randgrößen

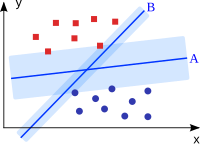
Eine Support Vector Machine dient als Klassifikator und Regressor. Eine Support Vector Machine unterteilt eine Menge von Objekten so in Klassen, dass um die Klassengrenzen herum ein möglichst breiter Bereich frei von Objekten bleibt; sie ist ein sogenannter Large Margin Classifier (dt. „Breiter-Rand-Klassifikator“).

Jedes Objekt wird durch einen Vektor in einem Vektorraum repräsentiert. Aufgabe der Support Vector Machine ist es, in diesen Raum eine Hyperebene einzupassen, die als Trennfläche fungiert und die Trainingsobjekte in zwei Klassen teilt. Der Abstand derjenigen Vektoren, die der Hyperebene am nächsten liegen, wird dabei maximiert. Dieser breite, leere Rand soll später dafür sorgen, dass auch Objekte, die nicht genau den Trainingsobjekten entsprechen, möglichst zuverlässig klassifiziert werden.

Lineare Trennbarkeit

Eine saubere Trennung mit einer Hyperebene ist nur dann möglich ist, wenn die Objekte linear trennbar sind. Diese Bedingung ist für reale Trainingsobjektmengen im Allgemeinen nicht erfüllt. Support Vector Machines überführen beim Training den Vektorraum und damit auch die darin befindlichen Trainingsvektoren in einen höherdimensionalen Raum, um eine nichtlineare Klassengrenze einzuziehen. In einem Raum mit genügend hoher Dimensionsanzahl – im Zweifelsfall unendlich – wird auch die verschachteltste Vektormenge linear trennbar.

Die Hochtransformation ist enorm rechenlastig und die Darstellung der Trennfläche im niedrigdimensionalen Raum im Allgemeinen unwahrscheinlich komplex und damit praktisch unbrauchbar. An dieser Stelle setzt der sogenannte Kernel-Trick an. Verwendet man zur Beschreibung der Trennfläche geeignete Kernelfunktionen, die im Hochdimensionalen die Hyperebene beschreiben und trotzdem im Niedrigdimensionalen „gutartig“ bleiben, so ist es möglich, die Hin- und Rücktransformation umzusetzen, ohne sie tatsächlich rechnerisch ausführen zu müssen.

Entscheidungsbäume

→ Hauptartikel: Entscheidungsbaum

Dieser einfache Klassifizierungsentscheidungsbaum sagt vorher, ob ein Apfelbaum Früchte tragen wird. Knoten sind grau dargestellt, Blätter grün.

Beim Lernen von Entscheidungsbäumen wird ein Entscheidungsbaum als Modell verwendet, um Schlussfolgerungen aus den Beobachtungen zu ziehen, die im Trainingsdatensatz enthalten sind. Gelernte Regeln werden durch Knoten und Zweige des Baums repräsentiert und Schlussfolgerungen durch seine Blätter. Ein Modell mit diskreten Ausgabewerten (in der Regel ganzen Zahlen) nennt man Klassifizierungsbaum, dabei repräsentieren die Blattknoten die Klassen und die Zweige UND-Verknüpfungen der Merkmale, die zu der Klasse führen. Ein Modell mit kontinuierlichen Ausgabewerten (in der Regel reellen Zahlen) nennt man Regressionsbaum. Der Algorithmus wählt beim Training diejenige Reihenfolge für die Abfrage der Merkmale, bei der das Modell bei jeder Verzweigung möglichst viel Information erhält. Nach dem Training kann man das Modell auch dazu verwenden, explizit und graphisch die Regeln darzustellen, die zu einer Entscheidung führen.

Der im Bild dargestellte Binärbaum benötigt als Eingabe einen Vektor mit den Merkmalen eines Apfelbaumes. Ein Apfelbaum kann beispielsweise die Merkmale alt, natürliche Sorte und reichhaltiger Boden besitzen. Beginnend mit dem Wurzelknoten werden nun die Entscheidungsregeln des Baumes auf den Eingabevektor angewendet. Gelangt man nach einer Folge ausgewerteter Regeln an ein Blatt, erhält man die Antwort auf die ursprüngliche Frage.

Random Forests

→ Hauptartikel: Random Forest

Ein Random Forest.

Ein Random Forest besteht aus mehreren unkorrelierten Entscheidungsbäumen. Ein Random Forest mittelt über mehrere Entscheidungsbäume, die auf verschiedenen Teilen desselben Trainingsdatensatzes trainiert wurden. Eine große Anzahl unkorrelierter Bäume macht genauere Vorhersagen möglich als ein einzelner Entscheidungsbaum. Dadurch wird in der Regel die Leistung des endgültigen Modells erheblich gesteigert.

Künstliche Neuronale Netze

→ Hauptartikel: Künstliches neuronales Netz

Ein künstliches neuronales Netz besteht aus einer Gruppe von künstlichen Neuronen, die miteinander verbunden sind. Im Bild zeigt jeder Kreis ein künstliches Neuron und jeder Pfeil eine Verbindung zwischen zwei künstlichen Neuronen.

Künstliche neuronale Netze (KNN) sind Modelle, deren Struktur von biologischen neuronalen Netzen, aus denen Tiergehirne bestehen, inspiriert wurde. Solche Modelle können aus komplexen und scheinbar zusammenhanglosen Informationen lernen. Einige erfolgreiche Anwendungen sind Bilderkennung und Spracherkennung.

Ein KNN wird von Einheiten oder Knoten gebildet, die miteinander verbunden sind. Die Knoten sind künstliche Neuronen. Ein künstliches Neuron empfängt Signale von anderen Neuronen und verarbeitet sie mit einer Aktivierungsfunktion. Jedem Eingangssignal ist ein Gewicht zugeordnet, das bestimmt, welchen Einfluss das Signal auf die Aktivierungsfunktion hat. Eine einfache Aktivierungsfunktion berechnet die Summe aller gewichteten Eingangssignale und legt sie als Signal auf alle Ausgänge, wenn sie einen bestimmten Schwellenwert überschreitet. Wenn die Summe unter dem Schwellenwert liegt, erzeugt diese Aktivierungsfunktion kein Ausgangssignal. Zu Beginn stehen alle Schwellenwerte und Gewichte auf Zufallswerten. Während des Trainings werden sie an die Trainingsdaten angepasst.

In der Regel werden die Neuronen in Schichten zusammengefasst. Die Signale wandern von der ersten Schicht (der Eingabeschicht) zur letzten Schicht (der Ausgabeschicht) und durchlaufen dabei möglicherweise mehrere Zwischenschichten (versteckte Schichten). Jede Schicht kann die Signale an ihren Eingängen unterschiedlich transformieren. Ein KNN mit vielen verborgenen Schichten wird auch als tiefes neuronales Netz bezeichnet. Darauf bezieht sich auch der Begriff Deep Learning.

Bekannte Beispiele für Architekturen, die KNN einsetzen, sind rekurrente neuronale Netze (RNN) für die Verarbeitung von Sequenzen, convolutional neural networks (CNN) für die Verarbeitung von Bild- oder Audiodaten und generative vortrainierte Transformer (GPT) für Sprachmodelle.

Generative Adversarial Networks

→ Hauptartikel: Generative Adversarial Networks

Schematische Darstellung eines Generative Adversarial Networks.

Generative Adversarial Networks (GAN) ist die Bezeichnung für eine Klasse von maschinellen Lernverfahren, die KNN im Kontext von generativem Lernen bzw. unüberwachtem Lernen trainieren. Ein GAN besteht aus zwei KNN, einem Generator und einem Diskriminator. Zuerst wird der Diskriminator darauf trainiert, zwischen echten Trainingsdaten und vom Generator aus einer zufälligen Eingabe erzeugten Daten zu unterscheiden. Danach wird der Generator darauf trainiert, aus einer zufälligen Eingabe Daten zu erzeugen, deren Eigenschaften denen der vorher vom Diskriminator gelernten Trainingsdaten so ähnlich sind, dass der Diskriminator sie nicht von ihnen unterscheiden kann. Mit diesem Verfahren kann beispielsweise ein GAN, das mit Fotografien trainiert wurde, neue Fotografien erzeugen, die für menschliche Betrachter zumindest oberflächlich authentisch aussehen und viele realistische Merkmale aufweisen. Obwohl sie ursprünglich als generatives Modell für unüberwachtes Lernen vorgeschlagen wurden, haben sich GANs auch für teilüberwachtes Lernen, überwachtes Lernen und bestärkendes Lernen als nützlich erwiesen.

Anforderungen

Im praktischen Einsatz ist das maschinelle Lernen oft ein wesentlicher Bestandteil eines Produktes. Die Auswahl von geeigneten Methoden und Modellen wird dann neben den Eigenschaften der Trainingsdaten auch von den Anforderungen an das Produkt eingeschränkt. Beispielsweise können für Vorhersagen zum Verbraucherverhalten, für lernende autonome Systeme oder für die Optimierung von industriellen Fertigungsketten unterschiedliche Zertifizierungen erforderlich sein.

Genauigkeit

Genauigkeit ist die wichtigste Anforderung. Wenn die geforderte Genauigkeit nicht erreicht werden kann, weil beispielsweise der Aufwand für die dafür erforderliche Datenerhebung zu groß wäre, dann braucht man weitere Anforderungen nicht mehr zu analysieren.

Transparenz und Erklärbarkeit

Wenn Transparenz gefordert wird, dann wird erwartet, dass klar ist, wo welche Daten wann verarbeitet und gelöscht werden. Erklärbarkeit liegt vor, wenn die Grundlage, auf der das Modell Entscheidungen trifft, nachvollziehbar ist. Letzteres ist beim Einsatz von Entscheidungsbäumen grundsätzlich möglich, bei tiefen neuronalen Netzen zur Zeit aber nicht. Neuronale Netze liefern zwar oft gute Ergebnisse, es gibt aber keine verständliche Erklärung dazu, wie diese Ergebnisse entstanden sind. Allerdings stößt man bei komplexen Aufgaben in der Praxis auch dann schnell an Grenzen, wenn eine vollständige Überprüfung grundsätzlich möglich wäre, beispielsweise beim Überprüfen von tiefen Entscheidungsbäumen oder bei dem Versuch, umfangreiche klassische Programme mit vielen Verzweigungen nachzuvollziehen.

Zusätzlich zu den gelernten Parametern des mathematischen Modells kann eine gründliche Analyse der Daten, die zum Training und zur Validierung verwendet wurden, Aufschluss darüber geben, welche Eigenschaften die Entscheidungen des Modells am stärksten beeinflussen. Siehe auch Ethik der Künstlichen Intelligenz und Explainable Artificial Intelligence.

Ressourcen

Bei Ressourcen geht es in erster Linie um die Zeit und die Energie, die für das Training und die Vorhersagen benötigt werden. Bei Echtzeitanwendungen kann das Einhalten einer geforderten Antwortzeit sogar wichtiger sein als die Genauigkeit.

Datenschutz und Datensicherheit

Es gibt oft eine enge Beziehung zwischen Ressourcenbedarf, Datenschutz und Datensicherheit. Beispielsweise kann man den Datenschutz erhöhen, indem man Daten anonymisiert und das Training auf lokalen Rechnern durchführt und nicht auf externen leistungsstärkeren Servern. Siehe auch Ethik der Künstlichen Intelligenz.

Freiheit und Autonomie

Beispiel: Ein Roboter, der sehen kann, ist grundsätzlich eine mobile Kamera. Um eine permanente Überwachung des Nutzers zu verhindern, sollten neue Bilder nur lokal verarbeitet werden und kurzfristig gelöscht werden. Siehe auch Ethik der Künstlichen Intelligenz.

Robustheit und Sicherheit

Robustheit und Sicherheit eines Systems können bewertet werden, indem man analysiert, mit welcher Wahrscheinlichkeit das System Fehler macht und wie schlimm die Folgen dieser Fehler sind.

Automatisiertes maschinelles Lernen

→ Hauptartikel: Automatisiertes maschinelles Lernen

Das Ziel des automatisierten maschinellen Lernens besteht darin, möglichst viele Arbeitsschritte zu automatisieren. Dazu gehören die Auswahl eines geeigneten Modells und die Anpassung seiner Hyperparameter.

Siehe auch

• Föderales Lernen
• Empirische Risikominimierung
• Transfer Learning

Literatur

• Andreas C. Müller, Sarah Guido: Einführung in Machine Learning mit Python. O’Reilly-Verlag, Heidelberg 2017, ISBN 978-3-96009-049-6. 
• Christopher M. Bishop: Pattern Recognition and Machine Learning. Information Science and Statistics. Springer-Verlag, Berlin 2008, ISBN 978-0-387-31073-2. 
• David J. C. MacKay: Information Theory, Inference and Learning Algorithms. Cambridge University Press, Cambridge 2003, ISBN 0-521-64298-1 (Online). 
• Trevor Hastie, Robert Tibshirani, Jerome Friedman: The Elements of Statistical Learning. Data Mining, Inference, and Prediction. 2. Auflage. Springer-Verlag, 2008, ISBN 978-0-387-84857-0 (stanford.edu [PDF]). 
• Thomas Mitchell: Machine Learning. Mcgraw-Hill, London 1997, ISBN 0-07-115467-1. 
• D. Michie, D. J. Spiegelhalter: Machine Learning, Neural and Statistical Classification. In: Ellis Horwood Series in Artificial Intelligence. E. Horwood Verlag, New York 1994, ISBN 0-13-106360-X. 
• Richard O. Duda, Peter E. Hart, David G. Stork: Pattern Classification. Wiley, New York 2001, ISBN 0-471-05669-3. 
• David Barber: Bayesian Reasoning and Machine Learning. Cambridge University Press, Cambridge 2012, ISBN 978-0-521-51814-7. 
• Arthur L. Samuel (1959): Some studies in machine learning using the game of checkers. IBM J Res Dev 3:210–229. doi:10.1147/rd.33.0210.
• Alexander L. Fradkov: Early History of Machine Learning. IFAC-PapersOnLine, Volume 53, Issue 2, 2020, Pages 1385-1390, doi:10.1016/j.ifacol.2020.12.1888.

Weblinks

Commons: Maschinelles Lernen – Sammlung von Bildern, Videos und Audiodateien

• Literatur von und über Maschinelles Lernen im Katalog der Deutschen Nationalbibliothek