Unruh (Uhr)

Unruh-Spirale-Schwingsystem

Eingebautes Schwingsystem (zu erkennen sind der Unruhkloben mit Stoßsicherung, Rücker und Spiralklötzchen sowie die Schraubenunruh mit Breguetspirale)

Unruhlager (nicht stoßgesichert); das Öl (gelb dargest.) wird durch Kapillarwirkung im Lager gehalten

Unruh ist die Kurzbezeichnung für ein Unruh-Feder-Schwingsystem, wie es in vielen mechanischen Uhrwerken verwendet wird. Sie ist eine weiterentwickelte Form des Torsionspendels mit Integration der Funktion der Unrast. Die Unruh ist ein drehbar gelagertes Rad und die Feder meist eine Spiralfeder (kurz Spirale genannt). Dieses Schwingsystem dient als Gangregler für Kleinuhren, ist erforderlich für mechanisch angetriebene tragbare Uhren, also Taschenuhren und Armbanduhren, auch Wecker, zudem Uhren in Fahrzeugen, z. B. Chronometer auf Schiffen. Aus Platzgründen wurde sie zunehmend auch für Wanduhren verwendet.

Die Feder wird so ausgelegt, dass ihr Moment proportional zum Drehwinkel der Unruh ist, so dass das System einen harmonischen Oszillator bildet. Die Unruh schwingt dadurch mit einer bestimmten Schwingungsdauer bzw. Frequenz um ihre Achse. Im Zusammenspiel mit der Hemmung der Uhr sorgt sie für das abwechselnde schrittweise Anhalten und Freigeben des Räderwerks (Laufwerks), das von einer Energiequelle (meist Federantrieb, siehe Federhaus) angetrieben wird (siehe auch Uhrwerk). Der schrittweise Ablauf (und damit der Lauf der Zeit) wird durch ein mit dem Räderwerk verbundenes Zeigerwerk angezeigt.

Die Idee der Verwendung der Unruh zusammen mit einer Spiralfeder wurde nach einem Vorschlag von Jean de Hautefeuille durch Christiaan Huygens entwickelt, 1675 wurde ihm dafür ein französisches Patent erteilt.

Vorläufer

Bis zur Erfindung geeigneter Hemmungs-Systeme hatte einzig die Pendeluhr eine zufriedenstellende Genauigkeit, konnte aber nur an einem unbewegten Aufstellort eingesetzt werden. Da (Schwerkraft-) Pendel eine ortsfeste Aufhängung erfordern, waren die erstmals im 15. Jahrhundert entwickelten tragbaren Uhren (siehe Nürnberger Ei) stattdessen mit kurzen Torsionspendeln ausgestattet. Diese wurden allerdings von jeder Bewegung des Trägers beeinflusst und hatten Tagesfehler bis zu mehreren Minuten. Die Erfindung des Torsionspendels als Taktgeber für tragbare Uhren wurde fälschlicherweise Peter Henlein zugeschrieben, war jedoch schon im frühen 15. Jahrhundert bekannt. Von Henlein stammt die älteste tragbare Uhr.

Aufbau

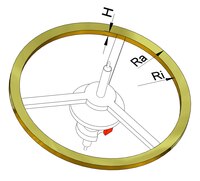
Das Schwingsystem besteht aus der eigentlichen Unruh oder Balance (Unruhwelle mit Lagerzapfen, Doppelrolle mit Hebelstein, Unruhring, Unruhschenkel) und der Spirale (mit Spiralklötzchen und Spiralrolle). Als Materialien kommen Stahl, Federstahl, Federbronze, Messing, insbesondere aber Speziallegierungen zum Einsatz, die möglichst unmagnetisch sein sollten, um den Einfluss äußerer Magnetfelder zu minimieren. In den letzten Umgang der Spirale greifen zwei sogenannte Rückerstifte (Rückerschlüssel) ein, die an einem auf dem Unruhkloben drehbaren Arm (Rücker) befestigt sind. Sie dienen der Regulierung der Schwingungsdauer.

Die Lagerung der Unruh erfolgt in zwei jeweils aus Loch- und Deckstein bestehenden (geölten) Lagern, die sich im Unruhkloben bzw. der Platine befinden. Bei guten Werken bestehen die Lager der Wellenzapfen aus Korunden, früher aus natürlichen Saphiren und Rubinen, heute aus synthetisch hergestellten, um einen möglichst reibungsarmen Gang zu ermöglichen. Die Unruhzapfen weisen einen sehr kleinen Durchmesser auf. Dadurch wird erreicht, dass die Zapfenreibung beim Anliegen des Zapfens am Lochstein (Reibmoment bei nicht senkrechter Lage der Unruhwelle) gering ist und sich nicht wesentlich unterscheidet von den Reibungsverhältnissen bei vertikaler Unruhwelle (Punktberührung des balligen Zapfens mit dem Deckstein). Der Gangunterschied bei verschiedenen Lagen der (tragbaren) Uhren wird so minimiert. Die geringe Zapfenreibung gewährleistet auch, dass die Schwingung nur schwach gedämpft und somit die (von der Hemmung periodisch zugeführte) Energie zur Aufrechterhaltung der Schwingung verringert wird (Gangreserve).

Der Nachteil der filigranen Zapfen besteht in der Bruchgefahr bei Stößen auf die Uhr. Darum werden die Zapfen trompetenartig geformt, um der Belastung besser standhalten zu können, was die Gefahr jedoch nicht vollständig beseitigt. Damit die Lagerzapfen bei Stößen nicht beschädigt werden, verwendet man eine Stoßsicherung, wie z. B. Parechoc oder Incabloc. Die Lagersteine sind dabei mit einer Feder beweglich gelagert und können Stößen ausweichen, wobei sich der kräftiger ausgebildete innere Teil der Unruhwelle an die Platine bzw. den Kloben anlegt und den größten Teil der Kraft überträgt. Für einfache Uhren sind sogenannte Körnerlager üblich (kegelförmiger Zapfen in kegelförmiger Lagerpfanne). Auch Sonderlager (z. B. magnetisch entlastet) sind bekannt.

Die (archimedische) Spirale ist vorgeformt und besitzt somit eine spannungsfreie Mittellage. Sie sollte mindestens zehn Windungen aufweisen. Die Spirale ist innen an der Spiralrolle befestigt, die mit der Unruhwelle (lösbar) verbunden ist. Das äußere Ende ist im Spiralklötzchen verstiftet, das im Unruhkloben bzw. der Unruhbrücke gehaltert wird. Auf der Doppelrolle (Doppelscheibe) befindet sich der Hebelstein (auch als Ellipse bezeichnet, meist aus Rubin gefertigt). Über diesen werden dem Schwingsystem einerseits die zur Aufrechterhaltung der Schwingung erforderlichen Antriebsimpulse vermittelt, anderseits schaltet er im Takt der Unruhschwingung die Hemmung. Dies gilt für die in tragbaren Uhren überwiegend eingesetzte Ankerhemmung. Bei weiteren Hemmungen (Spindelhemmung, Zylinderhemmung, Chronometerhemmung, Koaxialhemmung oder Co-Axial-Hemmung u. a.) werden diese beiden Aufgaben in anderer Weise realisiert.

Periode der Oszillation

Die Balance stellt eine träge Masse (Schwungmasse, Trägheitsmoment) dar. Wenn sie aus der durch die spannungsfreie Spirale bestimmten Mittellage ausgelenkt wird, entsteht durch die nun unter Spannung gesetzte (federnde) Spirale eine rücktreibende Kraft (exakter: ein Drehmoment) als Voraussetzung für die Schwingung. Sofern der Drehmomentverlauf in Abhängigkeit vom Auslenkwinkel linear (proportional) ist, schwingt das Schwingsystem harmonisch (Reibung vernachlässigt). Schwingungen mit kleinen und großen Amplituden besitzen in diesem Fall die gleiche Schwingungsdauer (Isochronismus). Dies ist ein erstrebenswerter Zustand, denn dem Schwingsystem können wegen des Drehmomentabfalls der die Uhr antreibenden Aufzugsfeder (Energiespeicher) während ihrer Entspannung keine konstant großen Antriebsimpulse zugeführt werden. Das hätte keine Auswirkungen auf die Ganggenauigkeit der Uhr, wenn Isochronismus realisiert werden könnte, was jedoch nur näherungsweise möglich ist. Man hat auch versucht, trotz des Drehmomentabfalls der Antriebsfeder die Antriebsimpulse konstant zu halten (siehe Zwischenaufzug). Das Schwingsystem schwingt dann ständig mit der gleichen Schwingungsweite und der Isochronismusfehler (also die Nichtlinearität) spielt keine Rolle.

• 
  Trägheitsmoment des Unruhrings
• 
  Querschnitt der Spiralklinge
• 
  Näherungsweise Berechnung der Spirallänge
• 
  Berechnung der Spirallänge

Die Periodendauer $T$ der Unruhschwingung hängt vom Trägheitsmoment $I$ der Unruh ab und vom Direktionsmoment $D$ ihrer Spirale:

$T=2\pi {\sqrt {\frac {I}{D}}}\,.$

Das Trägheitsmoment der Unruh wird von deren Gestaltung und den verwendeten Werkstoffen bestimmt. Für eine Abschätzung genügt es, nur den Unruhring zu berücksichtigen (siehe Bild). Der reale Wert des Trägheitsmoments ist dann etwas größer. Die Unruh schwingt also mit etwas geringerer Frequenz als berechnet. Unter dieser Voraussetzung gilt:

$I={\frac {1}{2}}m(R_{a}^{2}+R_{i}^{2})$

Die Masse $m$ des Rings berechnet sich zu:

$m=\rho \pi H(R_{a}^{2}-R_{i}^{2})$

$\rho$ ist die Dichte des verwendeten Werkstoffs (für Messing und Glucydur ca. $8{,}5\,\mathrm {\tfrac {g}{cm^{3}}}$).

Das Direktionsmoment für eine Spirale mit rechteckigem Klingenquerschnitt (Flächenträgheitsmoment $I_{S}$, Breite $b$, Höhe $h$, aktive Länge $l$, Elastizitätsmodul $E$) ergibt sich zu

$D={\frac {I_{S}E}{l}}={\frac {hb^{3}E}{12l}}$ (siehe Bild)

Der Elastizitätsmodul $E$ beträgt z. B. bei Nivarox-Spiralen ca. $200\,\mathrm {\tfrac {kN}{mm^{2}}}$ und bei Elinvar-Spiralen ca. $150\,\mathrm {\tfrac {kN}{mm^{2}}}$. Die Spirallänge $l$ kann mit guter Näherung berechnet werden, wenn man den mittleren Radius der vollen Windungen $n$ verwendet und das ggf. verbleibende Stück bis zum Rücker hinzuaddiert (vgl. Bild). Die Gleichung lautet dann:

$l=2\pi \left(r_{i}+{\frac {r_{a}-r_{i}}{2}}\right)n+{\frac {\pi r\beta }{180}}$

Bei exakter Berechnung der Spirallänge (siehe dazu Spirale oder) ist zu beachten, dass die entsprechende Formel für den Spiralenanfang im Nullpunkt gilt. Man muss also auch die Länge li vom Nullpunkt bis zur Spiralrolle berechnen und von der ermittelten Gesamtlänge abziehen (vgl. beigefügtes Bild).

Bei den Gleichungen ist vorausgesetzt, dass die Spirale in ihrem linearen Arbeitsbereich bleibt und die Dämpfung vernachlässigt werden kann. Ein (reziprokes) Maß für die Dämpfung ist der Gütefaktor – ein Qualitätsmerkmal des Uhrwerks. Eine geringe Güte bedeutet, dass pro Periode ein beträchtlicher Teil der enthaltenen Energie durch die Hemmung nachgeliefert werden muss. Das macht den Taktgeber empfindlich für Veränderungen der Federspannung der Aufzugsfeder. Eine hohe Güte mindert andererseits auch den Einfluss von periodischen Störungen, wenn etwa der Träger der Uhr winkt oder applaudiert.

Die übliche Schwingungsfrequenz beträgt 18.000 Halbschwingungen pro Stunde. In Serie hergestellte Schnellschwinger arbeiten mit bis zu 36.000 Halbschwingungen pro Stunde, bei Serienwerken sind jedoch meist 21.600 oder 28.800 Unruhhalbschwingungen pro Stunde verbreitet.

Prinzipiell gilt: Je höher die Frequenz, desto geringer sind solche Störungen. Daher bewirkte die Einführung der schnellschwingenden Unruh eine merkliche Verbesserung des Uhrgangs. Auch die möglichst große Schwingungsweite (Standard min. 220° pro Halbschwingung) trägt dazu bei, dass Störungen (z. B. durch die Hemmung) sich weniger stark auswirken, da die kinetische Energie des Schwingsystems im Bereich seiner Mittellage (wo der Hemmungseingriff mit der Energiezufuhr erfolgt) im Verhältnis zur Störung dann größer ist.

Probleme und Lösungen

Unruh

• 
  Kompensationsunruh mit Spiralfeder
• 
  Unruhwaage
• 
  Maschinell hergestellte Auswuchtfräsung an einer Unruh

Da die Schwingungsdauer wesentlich vom Trägheitsmoment der Unruh und von den Eigenschaften der Spirale abhängt, wirken sich Temperaturänderungen durch Maßänderungen und Änderung der Materialeigenschaften (Elastizitätsmodul der Spirale) auf die Ganggenauigkeit aus. Es wurden deshalb Kompensationsunruhen aus einem aufgeschnittenen Bimetall-Ring (meist aus Stahl kombiniert mit Messing) entwickelt. Kompensationsunruhen (genannt auch Bimetallunruhen) tragen am Unruhring Stellschrauben (siehe Kompensation). Von Nachteil war, dass die Kompensation nicht bei jeder Temperatur gleich ausgeprägt ist und nur bei zwei Temperaturen keine temperaturbedingte Gangabweichung erfolgt. Durch Einsatz spezieller temperaturstabiler Legierungen (Elinvar, Nivarox u. ä.) für Spiralfedern ist seit den 1930er Jahren die Notwendigkeit der Kompensation entfallen, so dass seit etwa 1960 zunehmend und heute nur noch monometallische Unruhen (meist aus Messing) eingesetzt werden.

Bei tragbaren Uhren verändert das Schwingsystem seine Lage. Ein außermittiger Schwerpunkt der Unruh wirkt je nach Lage der Uhr wie ein kleines Pendel und verursacht (außer bei genau senkrechter Lage der Unruhwelle) Gangabweichungen der Uhr. Es ist deshalb notwendig, dass die Unruh ausgewuchtet wird. Darunter versteht man die exakte Verlagerung des Schwerpunktes auf die Achse der Unruhwelle. Früher geschah das durch (mehrfachen) manuellen Materialabtrag am Unruhring oder aber (ähnlich wie bei der Kompensationsunruh) durch Verstellen von am Unruhring angeordneten Schrauben (Schraubenunruh). Die Kontrolle erfolgte mit einer Unruhwaage. Das waren mit großem Arbeitsaufwand verbundene Tätigkeiten. In der modernen Uhrenfertigung erfolgt das Auswuchten der Unruh maschinell mit einer einzigen Fräsung. Es werden zwar noch Schraubenunruhen gefertigt. Die Schrauben stellen jedoch nur Zierrat dar und sind funktionell nicht erforderlich.

Spirale

• 
  Unruhspiralentypen: (1) Flache Spirale, (2) Breguet Endkurve, (3) Chronometer-Helix mit gebogenen Enden in 2 Ansichten, (4) Frühe Unruhspiralen
• 
  Kraft bei Auslenkung der Spirale
• 
  Bewegung der Spirale
• 
  Verringerung des Fehlers bei größerer Windungszahl

In tragbaren Uhren werden flache Spiralen verbaut. Bei stationären Uhren (insbesondere Chronometern) kommen Wendelfedern (Helix) zum Einsatz (siehe Video).

Bei den früher für die Spirale verwendeten Werkstoffen spielte die Änderung des Elastizitätsmoduls bei Temperaturänderung eine große Rolle. Für präzise Uhren waren deshalb Kompensationsunruhen erforderlich. Moderne Spiralen bestehen aus Speziallegierungen, die praktisch keine Temperaturabhängigkeit mehr besitzen (neuerdings auch Siliziumwerkstoffe).

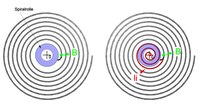
Die oben erwähnte wünschenswerte lineare Kennlinie für das rücktreibende Drehmoment M(α) der Spirale wäre gegeben, wenn sich bei beliebiger Verdrehung der Unruhwelle um α und einer am äußeren Spiralende wirkenden Kraft F(α) eine gleichmäßige Krümmungsänderung der gesamten Spirale ergäbe (gegenüber der Krümmung der spannungsfreien Mittellage).

Die Spirale würde dann konzentrisch schwingen („atmen“). Dazu müsste sich jedoch die Wirkungslinie der Kraft kontinuierlich während der Schwingung verlagern (z. B. von P nach P*, siehe Bild) und sich somit der Radius r(α) ändern. Die Spirale ist jedoch außen durch das Spiralklötzchen in einem festen Punkt P fixiert. Das hat zur Folge, dass keine gleichmäßige Krümmungsänderung möglich ist (wie im Bild zur Verdeutlichung übertrieben gezeigt) und demzufolge das rücktreibende Drehmoment eine nichtlineare Kennlinie aufweist (kein Isochronismus). Ferner verlagert sich dadurch der Schwerpunkt der Spirale, der auch in der Mittellage nicht auf der Achse der Unruhwelle liegt, während der Schwingung. Der exzentrische Spiralenschwerpunkt hat auf den Uhrengang eine ähnliche Wirkung wie der außermittige Unruhschwerpunkt, da er auch von der Gravitation beeinflusst wird.

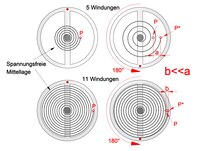
Bei Uhren mit normalen Anforderungen ist die durch die Nichtlinearität des rücktreibenden Drehmomentes verursachte Gangabweichung tolerabel, wenn die Spirale zehn oder mehr Windungen aufweist, weil dann die Abweichung von der idealen Krümmungsänderung nicht allzu groß ist (im Bild für eine Halbschwingung von 180° verdeutlicht).

Für präzise Uhren ist das jedoch nicht der Fall.

• 
  Breguetspirale (Prinzip)
• 
  Breguetspirale (Ausführung)
• Breguetspirale (Bewegung)

Breguet hat auf experimentellem Wege eine Möglichkeit gefunden, eine angenähert lineare Kennlinie zu erreichen. Vereinfacht gesagt, hat er die Spirale mit einer Zusatzfeder versehen (siehe Bild). Diese muss so geformt sein, dass

• sie eine Kraft F(α) auf die Spirale ausübt, die bei beliebigem Verdrehwinkel α genau der Kraft entspricht, die für eine gleichmäßige Krümmungsänderung der Spirale erforderlich ist;
• die Wirkungslinie der Kraft sich bei Verdrehung der Unruhwelle um α genau so verlagert, wie es die gleichmäßige Krümmungsänderung erfordert;
• die Wirkungslinie immer tangential zum Spiralende verläuft.

Das Federende der Zusatzfeder stellt dann gleichsam ein bewegliches Spiralklötzchen dar und bewegt sich bei Auslenkung auf dem gleichen Federweg wie das Ende der schwingenden Spirale bei deren gleichmäßiger Krümmungsänderung.

Zweckmäßigerweise hat Breguet die Zusatzfeder durch Verlängerung der Spirale und eine entsprechenden Formung dieser Verlängerung (Endkurve) realisiert. Dazu musste er notgedrungen die Endkurve in eine Ebene über der Spirale anheben, da ja sonst Spirale und Zusatzfeder kollidieren würden. Hierfür sind zwei Knicke anzubringen (siehe Bild). Auch kontinuierliche Verwindung ist möglich. Die Breguetspirale ist handwerklich schwierig zu fertigen. Auch Endkurven für das innere Ende der Spirale sind bekannt, werden aber nicht angewandt. Wendelfedern werden ebenfalls mit Endkurven versehen.

Lange Zeit nach Breguet hat Phillips das Endkurvenproblem theoretisch behandelt. Im Ergebnis hat er drei einfache Regeln aufgestellt:

• Die Endkurve muss sich tangential (knickfrei) an das Spiralende anschließen
• Der Schwerpunkt der Endkurve muss auf einer durch den Mittelpunkt (Unruhachse) gehenden Senkrechten zu einer Linie vom Mittelpunkt zum Spiralende liegen
• Das Produkt aus dem Schwerpunktabstand vom Mittelpunkt und der Endkurvenlänge muss gleich dem Quadrat des Abstandes des Spiralendes vom Mittelpunkt sein

• 
  Endkurvenbedingungen nach Phillips

Die Regeln gelten für den spannungsfreien Zustand (Mittellage). Nach diesen Regeln wurden Endkurven als Schablonenvorlagen entworfen (Gerstenberger), nach denen die Uhrmacher die Spiralen formen konnten. Dabei sind die theoretischen Kurven nach praktischen Erfahrungen geringfügig abgewandelt. Durch die Phillipskurven wird auch der Spiralenschwerpunkt auf die Achse der Unruhwelle verlagert und verbleibt dort während der Schwingung.

Mit neuzeitlichen Siliziumspiralen sind auch ohne Endkurven ähnliche Ergebnisse erreichbar. Durch die entsprechenden Fertigungsmethoden (Lasern, Ätzen usw.) können solche Spiralen mit über die Länge veränderlichem Querschnitt hergestellt werden, was ganz neue Gestaltungsmöglichkeiten eröffnet.

Rücker

Der Rücker ist eine einfache Möglichkeit, die Schwingungsdauer des Schwingsystems einzustellen. Ansonsten müsste durch mühevolles Aus- und Einstiften die Länge der Spirale den Erfordernissen angepasst werden. Durch Verschieben des Rückers wird die effektive (oder auch aktive) Spirallänge und damit die Schwingungsdauer verändert. Diese Länge reicht von der Spiralrolle bis zum Rücker. Der Bereich vom Rücker bis zum Klötzchen ist das „tote“ Spiralende, das (näherungsweise) keinen Einfluss auf die Schwingungsdauer hat. Die Spirale schwingt zwischen beiden Rückerstiften und legt sich an diese wechselweise an. Das bedeutet, dass während einer Schwingung verschiedene effektive Spirallängen wirksam werden. Bei Berührung der Rückerstifte ergibt sich eine verkürzte Länge. Das macht klar, dass durch den Rücker zwar eine einfache Möglichkeit der Regulierung gegeben, andererseits aber eine undefinierte Störquelle vorhanden ist (z. B. liegt bei großen Schwingungsweiten die Spirale länger an den Rückerstiften an als bei kleinen). Der erstrebte Isochronismus wird dadurch gestört. Das trifft auch auf Breguetspiralen zu, wo der Rücker auf die Endkurve (Zusatzfeder) wirkt.

Kompensation

Caspari und Grossmann haben Möglichkeiten entwickelt, auch mit Spiralen ohne Endkurve einen angenähert gleichmäßigen Gang der Uhr bei großen und bei kleinen Schwingungsweiten zu erreichen. Dazu werden gegensätzlich wirkende Störeinflüsse so abgestimmt, dass sich ihre Wirkungen gegenseitig kompensieren. Beispielsweise erzeugt das Spiel der Spirale im Rückerschlüssel ein Nachgehen der Uhr bei kleinen Schwingungsweiten, während eine bestimmte konstruktiv festgelegte Lage des inneren und äußeren Befestigungspunktes der Spirale zueinander ein Vorgehen zur Folge hat.

Hochwertige moderne mechanische Uhren werden sowohl mit flachen Spiralen nach Caspari und Grossmann als auch mit Breguetspiralen (Phillips-Endkurven) gefertigt.

Reglage

→ Hauptartikel: Reglage

Als Reglage bezeichnet man die Feinregulierung einer Uhr.

Zur Überprüfung der Reglage und damit der Ganggenauigkeit dient dem Uhrmacher eine Zeitwaage, ein Gerät, bei dem mit einem Körperschall-Mikrofon die Schwingung gemessen und grafisch dargestellt wird. Ein Micro-Dynagraph kann zur Aufzeichnung der Schwankungen des Kraftmomentes auf dem Hemmungsrad, der Veränderung der Schwingungsweite der Unruh und der Gangabweichungen der Uhr verwendet werden.

Literatur

• Otto Böckle, Wilhelm Brauns: Lehrbuch für das Uhrmacherhandwerk. Arbeitsfertigkeiten und Werkstoffe. 8.–10. Auflage. Wilhelm Knapp, Halle (Saale) 1951, (Reprint, herausgegeben von Michael Stern. Heel, Königswinter 2010, ISBN 978-3-86852-288-4).
• Hermann Brinkmann: Einführung in die Uhrenlehre (= Die Uhrmacherschule. Bd. 2). 10. unveränderte Auflage. Wilhelm Knapp, Düsseldorf 2005, ISBN 3-87420-010-8.
• George Daniels: Watchmaking. Updated 2011 edition. Philip Wilson Publishers, London 2011, ISBN 978-0-85667-704-5.
• Helmut Kahlert, Richard Mühe, Gisbert L. Brunner: Armbanduhren: 100 Jahre Entwicklungsgeschichte. Callwey, München 1983; 5. Auflage ebenda 1996, ISBN 3-7667-1241-1, S. 36–59.

Weblinks

Commons: Unruh – Sammlung von Bildern, Videos und Audiodateien

• Literatur von und über Unruh im Katalog der Deutschen Nationalbibliothek