Phasendiagramm

Phasendiagramme von Reinstoffen in der Druck-Temperatur-Ebene. Oben: „normales“ Verhalten – die Schmelzdruckkurve zwischen fester und flüssiger Phase hat eine positive Steigung. Unten: Reinstoff mit Dichteanomalie wie etwa Wasser– die Schmelzdruckkurve zwischen fester und flüssiger Phase hat eine negative Steigung.

Zustandsfläche eines Reinstoffes im Druck-Volumen-Temperatur-Zustandsraum. Eine aus Siede- und Kondensationskurve bestehende Binodale umschließt das blau kolorierte Koexistenzgebiet flüssig-gasförmig und erscheint in die Druck-Temperatur-Ebene projiziert als Tripelpunkt und kritischen Punkt verbindende Dampfdruckkurve.

Ein Phasendiagramm (auch Zustandsdiagramm, Zustandsschaubild oder Gleichgewichtsschaubild) ist eine Projektion von Phasengrenzlinien aus dem Zustandsraum eines thermodynamischen Systems in ein zweidimensionales kartesisches Koordinatensystem oder in ein Dreiecksdiagramm. Neben Phasengrenzlinien können Phasendiagramme auch Spinodalen enthalten. Phasendiagramme sind ein häufig genutztes Hilfsmittel in der Chemie, den Materialwissenschaften, der Physik und der Verfahrenstechnik, um das Phasenverhalten von Reinstoffen und Stoffgemischen graphisch darzustellen. Mögliche sich einstellende „metastabile Zustände“ werden in einem Phasendiagramm nicht berücksichtigt.

Reinstoffe (Einstoffsysteme)

Thermodynamische Einbettung

Komplexes Phasendiagramm des Reinstoffes ⁴He.

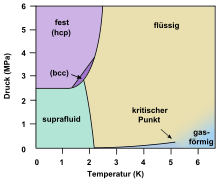
Die Menge aller im thermodynamischen Gleichgewicht liegenden Zustände eines Reinstoffes bildet in einem von Druck-, Temperatur- und Volumenachsen aufgespannten Zustandsraum eine Zustandsfläche, die sich in Druck-Temperatur-Volumen-Diagrammen darstellen lässt. Zustandsflächen von Reinstoffen können unter anderem folgende Merkmale enthalten:

• In den Zustandsflächen können Phasengrenzlinien liegen, bei deren Überquerung der Reinstoff Phasenübergänge durchläuft.
• Die Zustandsflächen können Koexistenzgebiete enthalten. Innerhalb der Koexistenzgebiete ist der Reinstoff in Form einer einzigen homogenen Phase instabil oder metastabil und liegt daher im thermodynamischen Gleichgewicht in Form von zumindest zwei koexistierenden Phasen vor. Phasengrenzlinien, die Koexistenzgebiete umschließen und dabei kritische Punkte als Extremwerte aufweisen, werden Binodalen genannt. Die den koexistierenden Phasen entsprechenden Zustände liegen dann auf der Binodale und werden durch Konoden verbunden. Innerhalb von Koexistenzgebieten, die durch Binodalen umschlossen werden, verlaufen Spinodalen, die an den kritischen Punkten die Binodalen berühren.
• Zustandsflächen können weiterhin Tripellinien enthalten, an denen feste Phase, flüssige Phase sowie Gasphase koexistieren.

Neben Phasengrenzlinien, an denen die Übergänge zwischen den Aggretatszuständen fest, flüssig und gasförmig stattfinden, können Phasendiagramme von Reinstoffen Phasengrenzlinien enthalten, an denen andere Arten von Phasenübergängen stattfinden. Beispiele sind:

• Phasenübergänge zwischen kristallinen Polymorphen in der festen Phase,
• Der Phasenübergang zwischen flüssigem und suprafluidem ⁴He,
• Übergänge zwischen ferromagnetischem oder ferroelektrischem Verhalten zu paramagnetischem oder paraelektrischem Verhalten bei der Curie-Temperatur.

Projektion in die Druck-Temperatur-Ebene

Weist die Zustandsfläche eines Reinstoffes Koexistenzgebiete auf, müssen Temperatur und Druck der dort im Gleichgewicht stehenden koexistierenden Phasen dieselben Werte aufweisen. Dies bedingt wiederum, dass die in die Druck-Temperatur-Ebene projizierten Phasengrenzlinien, die das Koexistenzgebiet begrenzen, dort aufeinander zu liegen kommen. Die Koexistenzgebiete erscheinen in der Druck-Temperatur-Ebene folglich als Linien. Phasendiagramme, die auf der Projektion des Zustandsraumes eines Reinstoffes in die Druck-Temperatur-Ebene basieren, können unter anderem folgende Elemente aufweisen:

• Der Tripelpunkt ist eine Projektion der parallel zur Volumenachse des Zustandsraums verlaufenden Tripellinie, die die Koexistenzgebiete von flüssiger Phase und Gasphase sowie von fester Phase und Gasphase voneinander trennt, in die Druck-Temperatur-Ebene.
• Die Siedekurve und die Kondensationskurve bilden eine Binodale, die das Koexistenzgebiet zwischen flüssiger Phase und Gasphase umschließt, wobei Siede- und Kondensationskurve am kritischen Punkt ineinander übergehen. Siede- und Kondensationskurve liegen in der Druck-Temperatur-Ebene genau übereinander und erscheinen dort als Dampfdruckkurve, die den Tripelpunkt und den kritischen Punkt verbindet.
• Der in der Druck-Temperatur-Ebene als Endpunkt der Dampfdruckkurve erscheinende kritische Punkt ist das Maximum der das Koexistenzgebiet aus flüssiger Phase und Gasphase umschließenden Binodalen.
• Die Sublimations- und Resublimationskurve begrenzen das Koexistenzgebiet von Feststoff und Gasphase. In der Druck-Temperatur-Ebene liegen beide Kurven aufeinander und erscheinen als Sublimationsdruckkurve, die den Nullpunkt der Druck-Temperatur-Ebene mit dem Tripelpunkt verbindet.
• Die Schmelzkurve und die Erstarrungskurve begrenzen das Koexistenzgebiet zwischen fester Phase und Flüssigkeit. In der Druck-Temperatur-Ebene liegen Schmelz- und Erstarrungskurve aufeinander und erscheinen als vom Tripelpunkt ausgehende Schmelzdruckkurve.

Projektion in die Druck-Volumen-Ebene

Mischungslücken mit zwei koexistierenden flüssigen Phasen in Zusammensetzungs-Temperatur-Phasendiagrammen binärer Mischungen. Schwarze Kurven: Binodalen. LCST: untere kritische Lösungstemperatur (lower critical solution temperature), UCST: obere kritische Lösungstemperatur (upper critical solution temperature).

Binodale (äußere Kurve) und Spinodale (innere Kurve) in einem Zusammensetzungs-Temperatur-Phasendiagramm eines binären Gemisches mit Mischungslücke.

Wird der Zustandsraum eines Reinstoffes in die Druck-Volumen-Ebene projiziert, zeigt das so erhaltene Phasendiagramm unter anderem das von Siede- und Kondensationskurve umschlossene Koexistenzgebiet von flüssiger Phase und Gasphase. Die aus Siede- und Kondensationskurve gebildete Binodale umschließt das Koexistenzgebiet von flüssiger Phase sowie Gasphase und weist am kritischen Punkt bei der kritischen Temperatur und dem kritischen Volumen ein Maximum auf. Innerhalb des Koexistenzgebietes kann die Spinodale eingezeichnet werden, die die äußeren Bereiche des Koexistenzgebietes, in denen eine homogene flüssige Phase oder eine homogene Gasphase metastabil ist, vom inneren Bereich des Koexistenzgebietes, in dem eine homogene flüssige Phase oder eine homogene Gasphase instabil ist, abtrennt. Binodale und Spinodale beziehungsweise deren Projektionen in die Druck-Volumen-Ebene lassen sich aus Van-der-Waals-Isothermen mit Hilfe der Maxwell-Konstruktion abschätzen. Im Verlauf von isothermen Zustandsänderungen bei Temperaturen unterhalb der kritischen Temperatur durchläuft der Reinstoff das Koexistenzgebiet entlang der parallel zur Volumenachse isotherm und isobar verlaufenden Konoden, welche die Zustandspunkte auf der Binodalen verbinden, die die miteinander im Gleichgewicht stehenden flüssigen und gasförmigen Phasen repräsentieren. Dabei findet ein Phasenübergang erster Ordnung statt. Im Falle einer isothermen Volumenexpansion verdampft der zunächst als Flüssigkeit vorliegende Reinstoff. Im Verlauf einer isothermen Volumenkompression kondensiert der zunächst als Gas vorliegende Reinstoff. Erfolgen isotherme Zustandsänderungen oberhalb der kritischen Temperatur, findet kein Phasenübergang statt – stattdessen ändert sich die Dichte des überkritischen Fluids kontinuierlich. Anstelle von Druck-Volumen-Phasendiagrammen sind auch Druck-Molvolumen-Phasendiagramme gebräuchlich, wobei die extensive Zustandsgröße Volumen durch die intensive Zustandsgröße Molvolumen ersetzt wird.

Mehrstoffsysteme

Thermodynamische Einbettung

Von Siede- und Taukurve eingeschlossenes Koexistenzgebiet flüssig/gasförmig im Temperatur-Zusammensetzungs-Phasendiagram eines binären Gemisches mit exemplarischen Konoden (rote Linien im Koexistenzgebiet). T_L: Siedetemp. Leichtsieder; T_S: Siedetemp. Schwersieder; Rechts rot markiert: Siedebereich einer 50 %-Mischung zwischen T₁ und T_S

Es werden verschiedene Arten von Gemischen unterschieden und zwar zeotrope, azeotrope und nahe azeotrope Gemische. Während der Verdampfung der zeotropen Gemische steigt die Temperatur an und im Gleichgewichtszustand haben der entstandene Dampf und die Flüssigkeit eine unterschiedliche Zusammensetzung.

Bei gegebenem Druck verdampft zu Beginn der Verdampfung der Stoff mit dem tieferen Siedepunkt stärker als der Stoff mit dem höheren Siedepunkt. Es ergibt daraus ein „Temperaturgleit“.

Azeotrope Gemische verhalten sich wie ein Reinstoff und die Siedetemperatur ändert sich während der Verdampfung des Gemischs nicht.

Mischungen können als homogene Mischphasen in verschiedenen Aggregatszuständen oder innerhalb einer Mischungslücke in Form koexistierender Phasen mit unterschiedlicher Zusammensetzung und/oder unterschiedlichen Aggregatzuständen vorliegen. Die Lage der Koexistenzlinien oder Koexistenzflächen im Zustandsraum eines Gemisches hängt sowohl von den Zustandsgrößen Druck, Temperatur und Volumen als auch von der Gemischzusammensetzung ab. Die Gemischzusammensetzung wird durch Angabe des Gehalts der einzelnen Komponenten, etwa in Form des Massenanteils, des Stoffmengenanteils oder des Volumenanteils, quantifiziert. Da die Summe der Massen-, Stoffmengen- oder Volumenanteile aller Komponenten eines Gemisches gleich eins ist, ist die vollständige Zusammensetzung eines aus $K$ Komponenten bestehenden Gemisches festgelegt, wenn der Gehalt von $K-1$ Komponenten angegeben wird. Daher umfasst der Zustandsraum eines aus $K$ Komponenten bestehenden Gemisches $K+2$ Dimensionen. Phasendiagramme von Gemischen stellen damit Projektionen von dreidimensionalen Schnitten durch höherdimensionale Zustandsräume in eine zweidimensionale Ebene dar.

In einem Mehrkomponentensystem sind im thermodynamischen Gleichgewicht die Temperatur und der Druck in allen Phasen gleich. Mit $P$ als Anzahl der koexistierenden Phasen ergeben sich $P(K-1)+2$ Variablen und $K(P-1)$ Bedingungsgleichungen. Die Zahl der Freiheitsgrade der Zustandsgrößen ergibt sich aus der Differenz zu $F=K-P+2$. Diese Interpretation wird Gibbssche Phasenregel genannt. In vielen technisch relevanten Fällen ist der Druck konstant und die Zahl der Freiheitsgrade um diesen reduziert auf $F=K-P+1$.

Binäre Gemische

Mischungslücken

Binäre Mischungen in Form von kondensierter Materie können als homogene Mischphase stabil sein oder im Gleichgewicht innerhalb einer Mischungslücke in Form koexistierender Phasen vorliegen, wobei homogene Mischphase und koexistierende Phasen denselben Aggregatzustand aufweisen (entweder fest oder flüssig), sich aber jeweils in ihrer stofflichen Zusammensetzung unterscheiden. Diejenigen Gleichgewichtszustände, in denen koexistierende Phasen stabil sind, bilden Mischungslücken, die jeweils eine Binodale von den Zuständen trennt, in denen eine homogene Mischphase stabil ist. Wird das binäre Gemisch durch eine Zustandsänderung, etwa durch eine Änderung von Druck, Temperatur, Volumen oder stofflicher Zusammensetzung, aus dem Einphasengebiet in eine Mischungslücke überführt, kommt es zu Entmischung. Umgekehrt bildet sich aus koexistierenden Phasen eine homogene Mischphase, wenn das binäre Gemisch aus einer Mischungslücke in das Einphasengebiet überführt wird. Mischungslücken werden häufig in Temperatur-Zusammensetzungs-Phasendiagrammen dargestellt. Die Zusammensetzung als diejenige Zustandsgröße, in der sich innerhalb der Mischungslücke die koexistierenden Phasen unterscheiden, wird entlang der x-Achse, und die Temperatur als diejenige Zustandsgröße, die in miteinander im Gleichgewicht stehenden koexistierenden Phasen denselben Wert haben muss, entlang der y-Achse eines zweidimensionalen kartesischen Koordinatensystems aufgetragen. Im Phasendiagramm werden mindestens die Binodalen eingetragen, wobei Minima der Binodalen kritische Punkte bei einer unteren kritischen Lösungstemperatur und Maxima der Binodalen kritische Punkte bei einer oberen kritischen Lösungstemperatur darstellen. Parallel zur Zusammensetzungs-Achse verlaufende Konoden verbinden diejenigen Zustandspunkte auf der Binodalen, die die bei der betreffenden Temperatur miteinander im Gleichgewicht stehenden koexistierenden Phasen repräsentieren. Die Schnittpunkte der Konoden mit der Binodalen markieren die Zusammensetzungen der koexistierenden Phasen. Ihr Mengenverhältnis kann mit Hilfe der Konodenregel ermittelt werden. Weiterhin können Spinodalen in den Phasendiagrammen eingezeichnet werden. Die Spinodalen trennen innerhalb von Mischungslücken Bereiche, in denen eine homogene Mischphase metastabil ist, von Bereichen, in denen eine homogene Mischphase instabil ist, ab.

Phasendiagramm Gold-Aluminium als Beispiel für ein binäres Gemisch aus zwei Metallen; rechts 100 % Gold, links 100 % Aluminium. Bei 59,5 Atom-% Gold befindet sich ein eutektischer Punkt.

Änderungen des Aggregatzustandes

Bildet sich in einem binären Gemisch aus einer homogenen Mischphase im Verlauf eines Phasenüberganges eine neue Phase mit einem anderen Aggregatzustand, durchläuft das binäre Gemisch in der Regel ein Koexistenzgebiet, in dem die ursprünglich als homogene Mischphase vorhandene Ausgangsphase und die sich neu bildende, in einem anderen Aggregatzustand vorliegende Zielphase koexistieren. Ausgangs- und Zielphase unterscheiden sich in ihrem Aggregatzustand sowie in ihrer stofflichen Zusammensetzung, müssen aber jeweils denselben Druck und dieselbe Temperatur besitzen. Sowohl in Temperatur-Zusammensetzungs-Phasendiagrammen als auch in Druck-Zusammensetzungs-Phasendiagrammen erscheint eine Projektion des Koexistenzgebietes, welche von Phasengrenzlinien eingefasst wird. Die den koexistierenden Phasen entsprechenden Zustände auf den ein Koexistenzgebiet einfassenden Phasengrenzlinien werden durch isotherm und isobar verlaufende Konoden verbunden. Die Schnittpunkte der Konoden mit den Phasengrenzlinien markieren die Zusammensetzungen der koexistierenden Phasen, während deren Mengenanteile mittels der Konodenregel ermittelt werden können. Technisch sind vor allem die Koexistenzgebiete zwischen festen Phasen und flüssiger Phase sowie zwischen flüssiger Phase und Gasphase von Interesse.

Koexistenzgebiet von flüssiger Phase und Gasphase

In einem thermodynamischen System wie einem binären Gemisch kann im Gleichgewicht nur eine Gasphase vorliegen. Sofern sich Koexistenzgebiete von flüssiger Phase und Gasphase sowie Mischungslücken, in denen zwei flüssige Phasen koexistieren, nicht überschneiden, finden Vedampfungs- und Kondensationsprozesse somit zwischen genau einer flüssigen und genau einer gasförmigen Phase statt. In Druck-Zusammensetzungs-Phasendiagrammen und Druck-Temperatur-Phasendiagrammen trennt die Siedekurve Zustände, in denen das binäre Gemisch ausschließlich in flüssiger Form vorliegt, vom Koexistenzgebiet der flüssigen Phase und der Gasphase ab. Die bei höheren Temperaturen auftretende Tau- oder Kondensationskurve trennt das Koexistenzgebiet von flüssiger Phase und Gasphase von den Zuständen ab, in denen das binäre Gemisch als homogene Gasphase vorliegt. Zustände, in denen das betrachtete thermodynamische System jeweils als Reinstoff vorliegt, definieren die beiden Endpunkte der Zusammensetzungs-Achse. Diese Zustände sind jeweils gemeinsame Punkte der das Koexistenzgebiet einfassenden Siede- und Kondensationskurven, die dort jeweils zusammenfallen. Davon abgesehen ist bei zeotropen Gemischen die Zusammensetzung der koexistierenden Phasen stets unterschiedlich. Dampfdruck und Siedetemperatur eines zeotropen Gemischs liegen stets zwischen den Dampfdrücken und Siedetemperaturen der entsprechenden Reinstoffe. Im Gegensatz dazu existieren binäre Gemische, deren Siede- und Kondensationskurven zumindest einen weiteren gemeinsamen Punkt aufweisen. An diesem Punkt weisen flüssige Phase und Gasphase dieselbe Zusammensetzung auf und werden als Azeotrop bezeichnet. Anwendung findet die Darstellung des Koexistenzgebietes der flüssigen Phase und der Gasphase in Druck-Zusammensetzungs- und Temperatur-Zusammensetzungs-Phasendiagrammen beispielsweise bei der Beschreibung, Auslegung und Berechnung von Destillationsprozessen.

Koexistenzgebiet zwischen festen Phasen und flüssiger Phase

Das Koexistenzgebiet von festen und flüssigen Phasen wird bei Schmelz- und Kristallisationprozessen durchlaufen, die in der Praxis in erster Linie durch Temperaturänderungen herbeigeführt werden. Die Soliduslinie grenzt Zustände, in denen das binäre Gemisch ausschließlich in Form fester Phasen vorliegt, vom Koexistenzgebiet, in dem feste und flüssige Phasen koexistieren, ab. Die bei höheren Temperaturen auftretende Liquiduslinie grenzt das Koexistenzgebiet von festen und flüssigen Phasen von den Zuständen ab, in denen das binäre Gemisch als homogene flüssige Phase vorliegt. Auch hier besteht in der Regel keine Überlappung mit einer Mischungslücke, in der zwei flüssige Phasen koexistieren, so dass sinnvollerweise das Vorhandensein einer einzigen flüssigen Phase vorausgesetzt werden kann. Diese kann jedoch wiederum mit mehreren koexistierenden festen Phasen im Gleichgewicht stehen. Druck-Zusammensetzungs- und Temperatur-Zusammensetzungs-Phasendiagramme sind geeignet, das Phasenverhalten von binären Mischungen darzustellen, die einen eutektischen Punkt aufweisen, an dem die flüssige Phase mit zwei festen Phasen koexistiert. Verfahrenstechnisch ist dies von Bedeutung, da ein Eutektikum, also ein binäres Gemisch mit der durch die Position des eutektischen Punktes definierten Zusammensetzung, einen niedrigeren Schmelzpunkt aufweist als jede andere Zusammensetzung des betreffenden binären Gemisches. Weiterhin durchläuft ein Eutektikum beim Erstarren oder Schmelzen durch Temperaturänderungen im Gegensatz zu allen anderen Zusammensetzungen des binären Gemisches kein Koexistenzgebiet. Darstellungen des Koexistenzgebietes der festen und flüssigen Phasen in Druck-Zusammensetzungs- und Temperatur-Zusammensetzungs-Phasendiagrammen sind weiterhin unter anderem im Zusammenhang mit dem Zonenschmelzverfahren von Interesse.

Dreiecksdiagramm des ternären Gemisches Au-Bi-Te. Gut erkennbar ist das dominierende Bismut sowie die große Lücke zwischen Maldonit und Gold.

Ternäre Gemische

Phasengrenzlinien werden aus den Zustandsräumen ternärer Gemische in der Regel in zweidimensionale Diagramme projiziert, die die Zusammensetzung der ternären Gemische für einen bestimmten Druck, eine bestimmte Temperatur und ein bestimmtes Volumen kartieren. Die Zusammensetzung ternärer Gemische kann im Prinzip mittels eines zweidimensionalen kartesischen Koordinatensystems, an dessen Koordinatenachsen die relativen Anteile von zwei der drei Komponenten des ternären Gemisches aufgetragen sind, in eindeutiger Weise dargestellt werden. In der Regel erfolgt die Darstellung der Zusammensetzung ternärer Gemische jedoch mit Hilfe von Dreiecksdiagrammen. Diese erlauben es, den Anteil jeder Komponente an einem ternären Gemisch jeweils an einer Koordinatenachse aufzutragen und entsprechend direkt abzulesen. An jeder Ecke eines Dreiecksdiagramms hat einer der Reinstoffe einen Anteil von 100 % am ternären Gemisch. Entspricht eine bestimmte Ecke eines Dreiecksdiagramms einem Anteil der Komponente $A$ am ternären Gemisch von 100 %, verlaufen Isolinien, die einem konstanten Anteil der Komponente $A$ am ternären Gemisch von weniger als 100 % entsprechen, parallel zur gegenüberliegenden Seite des Dreiecksdiagramms. Diese verbindet wiederum die Ecken, die jeweils einem Anteil von 100 % der Komponenten $B$ und $C$ am ternären Gemisch entsprechen. An einer der auf die Ecke, an der Komponente $A$ einen Anteil von 100 % am ternären Gemisch aufweist, zulaufenden Koordinatenachsen des Dreiecksdiagramms wird der Anteil von Komponente $A$ aufgetragen. Am Schnittpunkt der Isolinien mit dieser Koordinatenachse lässt sich der Anteil von Komponente $A$ am ternären Gemisch ablesen. Je größer der Abstand der Isolinie zur Ecke des Dreiecksdiagramms ist, an der das Gemisch zu 100 % Komponente $A$ enthält, desto niedriger ist der Anteil der Komponente $A$ am ternären Gemisch. Werden Binodalen, die Koexistenzbereiche umschließen, in ein Dreiecksdiagramm projiziert, sind die Konoden, die die auf den Binodalen lokalisierten Zustände der koexistierenden Phasen verbinden, in der Regel nicht parallel zu den Koordinatenachsen.

Siehe auch

• p-T-Diagramm
• p-v-Diagramm

Literatur

• Pablo G. Debenedetti: Metastable liquids: concepts and principles. Princeton University Press, Princeton, N.J. 1996, ISBN 0-691-08595-1. 
• Ulf W. Gedde: Essential Classical Thermodynamics (= SpringerBriefs in Physics). Springer International Publishing, Cham 2020, ISBN 978-3-03038284-1, doi:10.1007/978-3-030-38285-8 (springer.com [abgerufen am 9. Februar 2021]). 
• Andreas Heintz: Thermodynamik der Mischungen – Mischphasen, Grenzflächen, Reaktionen, Elektrochemie, äußere Kraftfelder. Springer-Verlag, Berlin/Heidelberg 2017, ISBN 978-3-662-49923-8, doi:10.1007/978-3-662-49924-5 (springer.com [abgerufen am 4. Februar 2021]). 
• Mats Hillert: Phase equilibria, phase diagrams and phase transformations: their thermodynamic basis. 2. Auflage. Cambridge University Press, Cambridge, UK 2008, ISBN 978-1-139-12921-3. 
• Bruno Predel, Michael Hoch, Monte Pool: Phase Diagrams and Heterogeneous Equilibria: a Practical Introduction. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 978-3-662-09276-7, doi:10.1007/978-3-662-09276-7. 

Weblinks

Commons: Phasendiagramme – Album mit Bildern

Erklärungen zu unter anderem zum kritischen Punkt, zum Tripelpunkt, zur Gibbs’schen Phasenregel und zu Zustandsdiagrammen von Wasser und Kohlenstoffdioxid:

• knapp, jedoch besonders in Bezug auf die Freiheitsgrade gut erklärt
• Mineralienatlas:Phasendiagramm
• weitere Phasendiagramme binärer Systeme

Videos zu Siede- und Schmelzdiagrammen:

• Video: Siedelinie, Taulinie und Azeotrop – Wie liest man Siedediagramme?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15680.
• Video: Konoden, Binodalen und invariante Punkte – Wie liest man Siedediagramme und Schmelzdiagramme?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15225.