Sekretärinnenproblem
In der Statistik, der Spieltheorie und der Entscheidungstheorie bezeichnet das Sekretärinnenproblem, auch bekannt als Heiratsproblem, die Aufgabe, aus einer Reihe einzeln und nacheinander betrachteter Bewerber den besten auszuwählen. Die Anzahl der Bewerber ist vorher bekannt. Dabei ist eine Ablehnung unwiderruflich. Wegen der enthaltenen Zufallselemente wird das Problem meist so formuliert, dass die größte Wahrscheinlichkeit für die Auswahl des besten Angebots zu bestimmen ist. Ein Lösungsalgorithmus für dieses Problem wird durch die Odds-Strategie gegeben. Die Lösung des Problems wird als 37-Prozent-Regel oder 1/e-Regel bezeichnet. Sie wurde von Geoffrey Miller in seinem Buch The Mating Mind beschrieben. Sie besagt, dass man die ersten Prozent der Bewerber betrachtet und danach den ersten Bewerber akzeptiert, der besser als alle bisherigen ist.
Der Nachteil dieser Strategie ist, dass die mittlere Platzierung des ausgewählten Bewerbers nicht optimal ist. Wenn der beste Bewerber unter den ersten 37 % der Bewerber ist, wird der letzte Bewerber genommen, der im Mittel keine gute Platzierung hat. Um die beste mittlere Platzierung zu erreichen, ist eine andere Strategie notwendig (siehe unten).
Problemstellung
[Bearbeiten | Quelltext bearbeiten]In einer häufig als Beispiel angeführten Variante möchte eine Organisation eine Sekretärin einstellen. Die Bewerberinnen werden nacheinander zum Gespräch eingeladen. In der Begutachtung wird eine Rangfolge (Platzierungen der Bewerberinnen) aufgestellt, und die Qualitäten einer jeden Bewerberin können festgehalten werden. Allerdings scheidet jede abgelehnte Bewerberin endgültig aus und steht im weiteren Verlauf nicht mehr zur Verfügung, eine Prämisse, die der tatsächlichen Personalbesetzungsrealität widerspricht. Die Wahrscheinlichkeit, die beste Bewerberin auszuwählen, soll maximiert werden.
Beispiel
[Bearbeiten | Quelltext bearbeiten]Es gibt drei Bewerberinnen, die sich in zufälliger Reihenfolge bewerben. Dabei sei 1 die schlechteste Bewerberin und 3 die beste. Für ihre beobachteten Qualitäten 1, 2, 3 gibt es dann 6 = 3! gleichwahrscheinliche Möglichkeiten: (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). Würde nun einfach die erste Bewerberin die Stelle bekommen, so wäre die Wahrscheinlichkeit, die beste einzustellen, gleich , nämlich in den Fällen (3,1,2) und (3,2,1).
Geschickter ist die folgende Strategie: Die erste Bewerberin wird abgelehnt. Falls die zweite besser als die erste ist, wird die zweite eingestellt, anderenfalls die dritte. Mit dieser Strategie bekommt man die beste Bewerberin in den Fällen (1,3,2), (2,3,1) und (2,1,3), also in 3 von 6 Fällen. Die Wahrscheinlichkeit ist somit .
Strategie
[Bearbeiten | Quelltext bearbeiten]Allgemein lässt sich zeigen, dass die folgende sehr einfache Strategie optimal ist:
- Betrachte die ersten der Bewerber mit und lehne sie ab.
- Wähle von den verbleibenden Bewerbern den ersten, der besser ist als jeder der ersten .
Es lässt sich zeigen, dass sich für große der optimale Wert für ergibt aus , wobei die Eulersche Zahl ist. Mit dieser Strategie liegt die Wahrscheinlichkeit, den besten Kandidaten zu wählen, bei , also etwa 37 %.
In etwa 63 % der Fälle findet man also nicht den besten Bewerber. Dies passiert, wenn der beste Bewerber bereits unter den ersten 37 % war (in diesem Fall wird der letzte Bewerber genommen) oder wenn der beste Bewerber später kommt, aber nach einem, der besser ist als der beste unter den ersten 37 % der Bewerber. Sollten die Bewerber zufälligerweise in qualitativ absteigender Rangfolge eingeladen werden, führt diese Strategie dazu, dass der schlechteste Bewerber genommen werden muss. Das Verfahren ist auch nicht sehr erfolgreich, wenn die ersten 37 % der Bewerber die schlechtesten waren. In diesem Fall wird der nächstbeste Bewerber akzeptiert.
Tabelle
[Bearbeiten | Quelltext bearbeiten]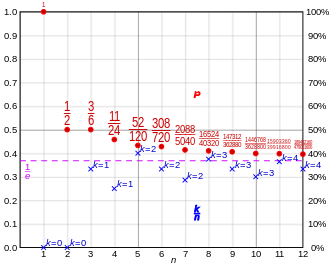
Folgende Tabelle zeigt die Anzahl der abgelehnten Bewerber, die maximalen Wahrscheinlichkeiten, die mittlere Platzierung des ausgewählten Bewerbers und die mittlere Anzahl der Einladungen für Bewerber:[1]
| n | r | Wahrscheinlichkeit | mittlere Platzierung | mittlere Anzahl der Einladungen |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0,5 | 1,5 | 1 |
| 3 | 1 | 0,5 | 1,6667 | 2,5 |
| 4 | 1 | 0,4583 | 1,875 | 2,8333 |
| 5 | 2 | 0,4333 | 2,2 | 4,1667 |
| 6 | 2 | 0,4278 | 2,3333 | 4,5667 |
| 7 | 2 | 0,4143 | 2,4762 | 4,9 |
| 8 | 3 | 0,4098 | 2,8125 | 6,2786 |
| 9 | 3 | 0,4060 | 2,9167 | 6,6536 |
| 10 | 3 | 0,3987 | 3,025 | 6,9869 |
| 11 | 4 | 0,3984 | ||
| 12 | 4 | 0,3955 | ||
| 13 | 5 | 0,3923 | ||
| 14 | 5 | 0,3917 | ||
| 15 | 5 | 0,3894 | ||
| 16 | 6 | 0,3881 | ||
| 17 | 6 | 0,3873 | ||
| 18 | 6 | 0,3854 | ||
| 19 | 7 | 0,3850 | ||
| 20 | 7 | 0,3842 |
Beweis
[Bearbeiten | Quelltext bearbeiten]
Der beste Bewerber kann die Wahl nur gewinnen, wenn er sich nicht unter den ersten Probekandidaten befindet. Kommt er direkt danach auf Platz , gewinnt er. Die Wahrscheinlichkeit, dass er auf diesem Platz steht, beträgt . Steht er einen Platz weiter auf Platz , wieder mit der Wahrscheinlichkeit , so gewinnt er genau dann, wenn sich der beste der vorherigen Kandidaten unter den ersten Probekandidaten befindet. Das ist mit der Wahrscheinlichkeit der Fall, zusammengesetzt gibt das die Wahrscheinlichkeit .
Geht man die Fälle entsprechend weiter durch bis zur letzten Position für den Besten, so erhält man wieder als Wahrscheinlichkeit für diese Position und für die Wahrscheinlichkeit, dass der beste Vorgänger zu den ersten Probekandidaten gehörte, die Wahrscheinlichkeit , zusammen also .
Insgesamt ergibt sich die Wahrscheinlichkeit für einen Erfolg der Strategie zu:
Für die Summe macht man die mit wachsendem immer besser werdende Integral-Näherung:
Das Maximum nimmt dieser Näherungsausdruck dort an, wo seine Ableitung gleich 0 ist, nämlich an der Stelle . Es beträgt . Das Maximum ist nicht sehr ausgeprägt: für den weiten Bereich wird nämlich durchweg nie unterschritten. Eine genauere auf der Odds-Strategie beruhende Analyse zeigt jedoch mehr, nämlich dass die Erfolgswahrscheinlichkeit immer strikt größer als ist, also stets strikt größer als die asymptotische Erfolgswahrscheinlichkeit, wenn die Anzahl der Bewerber gegen unendlich strebt.
Bezieht man den Zweitbesten in die obige Strategie mit ein, so nähert sich die Wahrscheinlichkeit dafür, dass dieser ausgewählt wird, für große dem Wert . Insgesamt wird damit die Wahrscheinlichkeit, dass man durch diese Strategie den besten oder zweitbesten Kandidaten erhält, für große etwas größer als 50 %.
Verallgemeinerungen und Varianten
[Bearbeiten | Quelltext bearbeiten]Unbekannte Anzahl N von Optionen
[Bearbeiten | Quelltext bearbeiten]Der Hauptnachteil des klassischen Sekretärinnenproblems für mögliche Anwendungen ist die Tatsache, dass die Anzahl der Optionen (Kandidaten) als im Voraus bekannt vorausgesetzt wird. Eine Möglichkeit, dies zu umgehen, ist anzunehmen, dass die Verteilung dieser Anzahl bekannt ist. In diesem Modell ist es jedoch im Allgemeinen schwieriger, die optimale Lösung zu bestimmen. Hinzu kommt insbesondere, dass die optimale Gewinnwahrscheinlichkeit oft wesentlich kleiner ist. Es ist intuitiv klar, dass die Unkenntnis der Anzahl von Optionen ihren Preis haben sollte, doch dieser Preis ist oft sehr hoch. Tatsächlich wird in einigen Fällen die optimale Gewinnwahrscheinlichkeit praktisch null. Eine geschickte Umformulierung dieses Modells löst dieses Problem.
1/e-Gesetz der besten Wahl
[Bearbeiten | Quelltext bearbeiten]Das 1/e-Gesetz der besten Wahl sollte nicht mit der oben erwähnten einfachen 1/e-Regel verwechselt werden, weil dieses erweiterte Modell für eine unbekannte Anzahl von Kandidaten gilt.
Das Wesentliche des umformulierten Modells, der sogenannte verallgemeinerte Ansatz in stetiger Zeit, beruht auf der Idee, dass es leichter ist, abzuschätzen wann Kandidaten mehr oder weniger wahrscheinlich kommen werden, unter der Hypothese, dass sie kommen, als die Verteilung der Anzahl selbst einzuschätzen.
Das verallgemeinerte Modell: Ein Kandidat ist im Zeitintervall aus einer unbekannten Anzahl von Kandidaten auszuwählen. Ziel ist es, die Wahrscheinlichkeit zu maximieren, bei gleich wahrscheinlichen Ankunftsreihenfolgen verschiedener Ränge den besten Kandidaten auszuwählen. Man nimmt an, dass alle Ränge unabhängig voneinander die gleiche Ankunftszeitdichte auf haben. Sei die entsprechende Ankunftszeitverteilung, d. h.
- , .
Das 1/e-Gesetz besagt dann: Sei die Lösung der Gleichung . Weiterhin sei S die Strategie, alle Kandidaten bis zur Zeit abzuwarten und dann, wenn möglich, den ersten Kandidaten auszuwählen, der besser ist als alle Vorgänger vor der Zeit .
Diese sogenannte 1/e-Strategie S hat folgende Eigenschaften:
- Wenn es zumindest einen Kandidaten gibt, dann gilt
- S erzielt für alle eine Gewinnwahrscheinlichkeit von mindestens
- S ist die einzige Strategie, die diese untere Schranke erreichen kann, und diese untere Schranke ist scharf
- S wählt keinen Kandidaten mit der Wahrscheinlichkeit
Das 1/e-Gesetz wurde mit Überraschung aufgenommen, denn eine Gewinnwahrscheinlichkeit von 1/e schien für eine unbekannte Anzahl von Kandidaten nicht realisierbar, wohingegen dieser Wert nun als untere Schranke gilt, und dies sogar in einem Modell mit anerkannterweise schwächeren Hypothesen. Das 1/e-Gesetz wird gerne mit der Lösung des Sekretärinnenproblems verwechselt, weil 1/e dort eine ebenfalls wichtige Rolle spielt. Man beachte jedoch, dass das 1/e-Gesetz wesentlich weiter geht, da es einerseits für eine unbekannte Anzahl von Kandidaten gilt und zudem einem anwendungsfreundlichen Modell in kontinuierlicher Zeit entspringt.
Beste mittlere Platzierung
[Bearbeiten | Quelltext bearbeiten]Wenn die Aufgabe stattdessen darin besteht, bei einer vorher bekannten Anzahl von Kandidaten im Mittel einen Kandidaten mit einer möglichst guten Platzierung auswählen, ist folgende Strategie notwendig:
- Es wird zunächst eine bestimmte Anzahl von Kandidaten abgelehnt.
- Anschließend wird der erste Kandidat akzeptiert, der unter den bisher betrachteten Kandidaten mindestens eine bestimmte Platzierung erreicht.
Diese Platzierungen, jeweils die mittlere Platzierung für den ausgewählten Kandidaten und die mittlere Anzahl der Einladungen sind für bis zu 16 Kandidaten in folgender Tabelle aufgelistet:[2]
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | mittlere Platzierung | mittlere Anzahl der Einladungen |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | |||||||||||||||
| 2 | 1 | 1,5 | 1 | |||||||||||||||
| 3 | - | 1 | 3 | 1,667 | 2,5 | |||||||||||||
| 4 | - | 1 | 2 | 4 | 1,875 | 2,667 | ||||||||||||
| 5 | - | 1 | 1 | 2 | 5 | 2,050 | 3 | |||||||||||
| 6 | - | - | 1 | 2 | 3 | 6 | 2,217 | 4,133 | ||||||||||
| 7 | - | - | 1 | 1 | 2 | 3 | 7 | 2,276 | 4,617 | |||||||||
| 8 | - | - | 1 | 1 | 2 | 2 | 4 | 8 | 2,4 | 4,752 | ||||||||
| 9 | - | - | - | 1 | 1 | 2 | 3 | 4 | 9 | 2,496 | 6,093 | |||||||
| 10 | - | - | - | 1 | 1 | 2 | 2 | 3 | 5 | 10 | 2,558 | 6,294 | ||||||
| 11 | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 5 | 11 | 2,614 | 6,743 | |||||
| 12 | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 6 | 12 | 2,684 | 6,809 | ||||
| 13 | - | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 6 | 13 | 2,735 | 8,256 | |||
| 14 | - | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 5 | 7 | 14 | 2,783 | 8,348 | ||
| 15 | - | - | - | - | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 7 | 15 | 2,818 | 8,754 | |
| 16 | - | - | - | - | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 4 | 5 | 8 | 16 | 2,871 | 8,940 |
Siehe auch
[Bearbeiten | Quelltext bearbeiten]- Entscheidung unter Unsicherheit
- Gefangenenparadoxon
- Odds-Strategie
- Umtauschparadoxon
- Ziegenproblem
- Zwei-Zettel-Spiel
- Gesetz der kleinen Zahlen
- Ski-Rental-Problem
Literatur
[Bearbeiten | Quelltext bearbeiten]- Eugene Dynkin: Optimal choice of the stopping time of a Markov process. In: Sov. Math. Dokl. Nr. 02, 1963, S. 238–240.
- Franz Thomas Bruss: Sum the Odds to One and Stop. In: Annals of Probability. Band 28, Nr. 03, 2000, S. 1384–1391.
- Franz Thomas Bruss: A Note on Bounds for the Odds Theorem of Optimal Stopping. In: Annals of Probability. Band 31, Nr. 04, 2003, S. 1859–1861.
- Franz Thomas Bruss: A Unified Approach to a Class of Best Choice Problems with an Unknown Number of Options. In: Annals of Probability. Band 12, Nr. 3, 1984, S. 882–889.
- Franz Thomas Bruss: Strategien der besten Wahl. In: Spektrum der Wissenschaft. Nr. 05, 2004, S. 102–104 (spektrum.de).
- Stephen M. Samuels: A Best-Choice Problem with Linear Travel Cost. In: Journal of the American Statistical Association. Band 80, Nr. 390, 1985, S. 461–464, doi:10.1080/01621459.1985.10478141.
- Eric W. Weisstein: Sultan’s Dowry Problem. In: MathWorld. Wolfram, 2004 (mathworld.wolfram.com [abgerufen am 24. Februar 2007]).
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Mathematik-Online: Sekretärinnenproblem
- Lieses Verehrer oder das „Sekretärinnen-Problem“ (PDF; 120 kB)
- Robert J. Vanderbei, Princeton University: The postdoc variant of the secretary problem
- Roberto Brera, Feng Fu: The satisficing secretary problem: when closed-form solutions meet simulated annealing
- GeeksforGeeks: Secretary Problem (A Optimal Stopping Problem)
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Kyle Siegrist, Random Services: The Secretary Problem
- ↑ Werner Brefeld: Mathematik im Alltag (nützliche Beispiele) - Hauskauf oder Arbeitsstellensuche (Entscheidungsstrategie)




























![{\displaystyle [0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ccef2d3dc751e081375d51c111709d8a1d7ac6)





