Ausreißer

Ein Ausreißer-Messwert. Die blaue Gerade wurde ohne Einbeziehung des Ausreißers erstellt, die violette mit der Einbeziehung.

Der Boxplot auf einem Zahlenstrahl dargestellt.

In der Statistik nennt man einen Messwert, der stark von der gesamten Messreihe abweicht, Ausreißer. Dies passiert, wenn ein Messwert einer Messreihe, die zur Ermittlung der Verteilung einer Zufallsgröße $X$ dienen soll, nicht aus dieser, sondern aufgrund eines Störeinflusses aus einer anderen Zufallsgröße $X'$ stammt. Hierdurch würde die Berücksichtigung dieses Messwertes zu einer Verfälschung führen, da so Stichproben zweier verschieden verteilter Zufallsgrößen gemischt würden. Die robuste Statistik beschäftigt sich mit der Ausreißerproblematik. Auch im Data-Mining beschäftigt man sich mit der Erkennung von Ausreißern. Von Ausreißern zu unterscheiden sind einflussreiche Beobachtungen.

Überprüfung auf Messfehler

Liegt ein Ausreißer vor, muss überprüft werden ob es sich bei dem Ausreißer tatsächlich um ein verlässliches und echtes Ergebnis handelt oder ob ein Messfehler vorliegt.

Beispiel: So wurde das Ozonloch über der Antarktis einige Jahre zwar bereits gemessen, die Messwerte aber als offensichtlich falsch gemessen bewertet (d. h. als „Ausreißer“ interpretiert und ignoriert) und dadurch nicht in ihrer Tragweite erkannt.

Ausreißertests

Ein anderer Ansatz wurde u. a. von Ferguson im Jahr 1961 vorgeschlagen. Danach wird davon ausgegangen, dass die Beobachtungen aus einer hypothetischen Verteilung stammen. Ausreißer sind dann Beobachtungen, die nicht aus der hypothetischen Verteilung stammen. Die folgenden Ausreißertests gehen alle davon aus, dass die hypothetische Verteilung eine Normalverteilung ist und prüfen, ob einer oder mehrere der Extremwerte nicht aus der Normalverteilung stammen:

• Ausreißertest nach Grubbs
• Ausreißertest nach Nalimov
• Ausreißertest nach David, Hartley und Pearson
• Ausreißertest nach Dixon
• Ausreißertest nach Hampel
• Ausreißertest nach Baarda
• Ausreißertest nach Pope

Der Ausreißertest nach Walsh basiert hingegen nicht auf der Annahme einer bestimmten Verteilung der Daten. Im Rahmen der Zeitreihenanalyse können Zeitreihen, bei denen ein Ausreißer vermutet wird, darauf getestet werden und dann mit einem Ausreißermodell modelliert werden.

Unterschiede zu Extremwerten

Ein beliebter Ansatz ist es, den Boxplot zu nutzen, um Ausreißer zu identifizieren. Die Beobachtungen außerhalb der Whisker werden dabei willkürlich als Ausreißer bezeichnet. Für die Normalverteilung kann man ausrechnen, dass knapp 0,7 % der Masse der Verteilung außerhalb der Whiskers liegen. Bereits ab einem Stichprobenumfang von $n>143$ würde man daher mindestens eine Beobachtung außerhalb der Whiskers erwarten (oder auch $k$ Beobachtungen außerhalb der Whiskers bei $n>143{,}3362\cdot k$). Sinnvoller ist es daher, statt von Ausreißern von Extremwerten zu sprechen.

Multivariate Ausreißer

Ausreißer rechts unten im Streudiagramm und Boxplots für jede einzelne Variable.

In mehreren Dimensionen wird die Situation noch komplizierter. In der Grafik rechts kann der Ausreißer rechts unten in der Ecke nicht durch Inspektion jeder einzelnen Variable erkannt werden; er ist in den Boxplots nicht sichtbar. Trotzdem wird er eine lineare Regression deutlich beeinflussen.

Andrews’ Kurven

Andrews’ Kurven mit unterschiedlich eingefärbten Daten

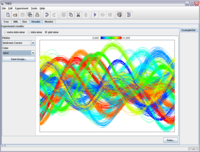
Andrews (1972) schlug vor, jede multivariate Beobachtung $(x_{i1},x_{i2},\dotsc ,x_{ip})$ durch eine Kurve zu repräsentieren:

$f_{i}(t)={\frac {x_{i1}}{\sqrt {2}}}+x_{i2}\sin(t)+x_{i3}\cos(t)+x_{i4}\sin(2t)+x_{i5}\cos(2t)+\dotsb$

Damit wird jede multivariate Beobachtung auf eine zweidimensionale Kurve im Intervalls $[-\pi ;\pi ]$ abgebildet. Aufgrund der Sinus- und Kosinusterme wiederholt sich die Funktion $f_{i}(t)$ außerhalb des Intervalls $[-\pi ;\pi ]$.

Für jeweils zwei Beobachtungen $i$ und $j$ gilt:

$\underbrace {\int _{-\pi }^{\pi }\left(f_{i}(t)-f_{j}(t)\right)^{2}dt} _{(1)}=\underbrace {\pi \sum _{k=1}^{p}(x_{ik}-x_{jk})^{2}} _{(2)}$

Der Ausdruck (1) links neben dem Gleichheitszeichen entspricht (zumindest approximativ) der Fläche zwischen den beiden Kurven, und der Ausdruck (2) rechts ist (zumindest approximativ) der multivariate euklidische Abstand zwischen den beiden Datenpunkten.

Ist also der Abstand zwischen zwei Datenpunkten klein, dann muss auch die Fläche zwischen den Kurven klein sein, d. h., die Kurven der Funktionen $f_{i}(t)$ und $f_{j}(t)$ müssen nahe beieinander verlaufen. Ist jedoch der Abstand zwischen zwei Datenpunkten groß, muss auch die Fläche zwischen den Kurven groß sein, d. h., die Kurven der Funktionen$f_{i}(t)$ und $f_{j}(t)$ müssen sehr unterschiedlich verlaufen. Ein multivariater Ausreißer würde als Kurve sichtbar sein, die sich von allen anderen Kurven in ihrem Verlauf deutlich unterscheidet.

Andrews’ Kurven haben zwei Nachteile:

• Wenn der Ausreißer in genau einer Variable sichtbar ist, nimmt der Mensch die unterschiedlichen Kurven umso besser wahr, je weiter vorne diese Variable auftaucht. Am besten sollte sie die Variable $x_{\bullet 1}$ sein. D.h., es bietet sich an, die Variablen zu sortieren, z. B. $x_{\bullet 1}$ wird die Variable mit der größten Varianz, oder man nimmt die erste Hauptkomponente.
• Wenn man viele Beobachtungen hat, müssen viele Kurven gezeichnet werden, sodass der Verlauf einer einzelnen Kurve nicht mehr sichtbar wird.

Stahel-Donoho Outlyingness

Stahel (1981) und David Leigh Donoho (1982) definierten die sog. Outlyingness. "Um die Maßzahl zu erhalten, die aussagt, wie weit ein Beobachtungswert von der Masse der Daten entfernt liegt, müssen alle möglichen Linearkombinationen $\alpha _{1}x_{i1}+\alpha _{2}x_{i2}+\dotsb +\alpha _{p}x_{ip}=\alpha ^{T}x_{i}$berechnet werden. Das heißt die Projektion des Datenpunktes auf den Vektor $\alpha$, mit $\sum _{k=1}^{p}\alpha _{i}^{2}=1$ ergibt die Outlyingness:

$\operatorname {out} (x_{i})=\sup _{\alpha }\left(\operatorname {out} (x_{i},\alpha )\right)=\sup _{\alpha }\left({\frac {\alpha ^{T}x_{i}-\operatorname {median} (\alpha ^{T}x)}{\operatorname {mad} (\alpha ^{T}x)}}\right)$,

Wobei der Median der projizierten Punkte ($\operatorname {median} (\alpha ^{T}x)$) und die mittlere absolute Abweichung der projizierten Punkte ($\operatorname {mad} (\alpha ^{T}x)$), als robustes Streuungsmaß angegeben wird. Der Median dient dabei als robustes Lage-, die mittlere absolute Abweichung als robustes Streuungsmaß. $\operatorname {out} (x_{i},\alpha )$ ist eine Normalisierung.

In der Praxis wird die Outlyingness berechnet, indem für mehrere hundert oder tausend zufällig ausgewählte Projektionsrichtungen $\alpha$ das Maximum $\operatorname {out} (x_{i},\alpha )$ bestimmt wird.

Ausreißererkennung im Data-Mining

Unter dem englischen Begriff Outlier Detection (deutsch: Ausreißererkennung) versteht man den Teilbereich des Data-Mining, bei dem untypische und auffällige Datensätze identifiziert werden. Anwendung hierfür ist beispielsweise die Erkennung von (potentiell) betrügerischen Kreditkartentransaktionen in der großen Menge der validen Transaktionen. Die ersten Algorithmen zur Ausreißererkennung waren eng an den hier erwähnten statistischen Modellen orientiert, jedoch haben sich aufgrund von Berechnungs- und vor allem Laufzeitüberlegungen die Algorithmen davon entfernt. Ein wichtiges Verfahren hierzu ist der dichtebasierte Local Outlier Factor.

Ausreißer lassen sich auch durch den Vergleich mit Prognoseintervallen entdecken.

Siehe auch

• M-Schätzer

Literatur

• Ausreißerproblem (outlier problem). In: P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, S. 16–18. 
• Vic Barnett, Toby Williams: Outliers in Statistical Data (= Wiley Series in Probability and Mathematical Statistics). 3. Auflage. Wiley, Chichester 1994, ISBN 0-471-93094-6. 
• R. Khattree, D. N. Naik: Andrews Plots for Multivariate Data: Some New Suggestions and Applications. In: Journal of Statistical Planning and Inference. Band 100, Nr. 2, 2002, S. 411–425, doi:10.1016/S0378-3758(01)00150-1. 

Weblinks

Wiktionary: Ausreißer – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Grundlagen der Statistik Ausreißertests
• Learning by Simulations Simulation der Auswirkung eines Ausreißers auf die lineare Regression