Benutzer:Ariser/Stehwellenverhältnis Alternativentwurf

Das Stehwellenverhältnis (englisch standing wave ratio, SWR) ist das Verhältnis von Maximalspannung zu Minimalspannung, die auf einem Wellenleiter, beispielsweise einem Koaxialkabel gemessen werden können. Dabei sind diese Spannungen je nach Leiterart zwischen Schirm und Signal oder zwischen zwei gegensätzlich gepolten Adern zu messen. In der Regel wird der Effektivwert der Spannungen gemessen. Ursache ist meist die teilweise Reflexion von Wellenenergie am Kabelende oder an einer Verbindung.

Bei einem SWR ≈ 1 wird fast die gesamte eingespeiste Leistung sofort am Kabelende vom Verbraucher absorbiert und zunächst nur wenig zur Quelle reflektiert. Bei einem grossen SWR wird ein hoher Anteil der eingespeisten Leistung am Verbraucher reflektiert und über den Wellenleiter zur Quelle zurück geleitet. Abhängig von deren Impedanz wird dieser Anteil dort absorbiert oder wieder teilweise zum Verbraucher reflektiert. Dann erzeugt ein grosses SWR in Datenkabeln störende Signalreflexionen.

Stehwellenverhältnis von Impulsen und kurzen Wellenpaketen

Am einfachsten lässt sich das SWR mit einem Einzelpuls wie im nebenstehenden Bild erklären. An der Sprungstelle der Impedanz wird ein Teil der von links eintreffenden Energie nach links zurück reflektiert. Die nach rechts weiter laufende Energie wird als Transmission bezeichnet.

An einem Messpunkt nahe dem linken Bildrand kann man (mit einem Oszilloskop) zu unterschiedlichen Zeiten die Amplitude U_Vor des vorlaufenden Signals und später die Amplitude U_Refl des reflektierten Signals messen. Das ist die Grundlage der Zeitbereichsreflektometrie. Im gezeigten Beispiel tritt eine Polaritätsumkehr auf, weil die Impedanz rechts von der Sprungstelle kleiner ist als links (Kurzschlusscharakteristik). Wäre die Impedanz rechts größer als links, hätten alle Impulse das gleiche Vorzeichen (Leerlaufcharakteristik).

Dem Bild entnimmt man U_Refl ≈ -0,5·U_Vor, an der Sprungstelle wird also 25 % der eintreffenden Leistung reflektiert. Das SWR berechnet man mit den Beträgen der Spannungen und es ergibt sich SWR = 3. Bei ausreichendem Zeitabstand aufeinander folgender Impulse kommt es an keinem Ort des Wellenleiters zu einer Überlagerung von vor- und rücklaufendem Impuls.

Für kurze Wellenpakete gilt Vergleichbares. U_Vor und U_Refl werden am gleichen Ort zu unterschiedlichen Zeiten gemessen, um Überlagerungseffekte zu vermeiden, wie sie im nebenstehenden Bild gezeigt werden.

Stehwellverhältnis von kontinuierlichen Wellen

Ein Dauersignal konstanter Frequenz kann man sich als alternierende Folge von Einzelpulsen vorstellen. Mangels längerer Pausen überlagern sich einlaufende und reflektierte Welle längs des gesamten Wellenleiters, wenn ein Teil der Energie reflektiert wird. Die entstehende Interferenz der gegenläufigen Wellen bewirkt an gewissen vorhersagbaren Stellen konstruktive Interferenz, wodurch die messbare Effektivspannung besonders hohe Werte erreicht. Folgende Längenangaben werden immer vom Kabelende in Richtung Sender gemessen:

Wenn der Lastwiderstand größer als der Wellenwiderstand des Kabel ist, misst man bei x =0 (also am Kabelende) ein Spannungsmaximum U_Max, ebenso bei n·λ/2 mit n = 1, 2, 3,..
Dazwischen, also bei ungeraden Vielfachen von λ/4 misst man wegen destruktiver Interferenz besonders geringe Spannungen U_Min.
Wenn der Lastwiderstand kleiner als der Wellenwiderstand des Kabel ist, kehren sich die Verhältnisse um. Bei kurzgeschlossenem Kabelende misst man dort selbstverständlich U = 0 und auf dem Kabel bildet sich eine Stehende Welle mit SWR = ∞.

Bei kontinuierlichen Wellen gibt es keinen Ort auf dem Wellenleiter, an dem sich (analog zu Einzelpulsen) U_Vor und U_Refl getrennt messen lassen, weil sich an jeder Stelle und zu jedem Zeitpunkt einlaufenden Welle und reflektierte Welle überlagern. Deshalb gibt es unterschiedliche Verfahren, die notwendigen Spannungswerte zu messen:

Unmittelbare Spannungsmessung

Man sucht - wie eben beschrieben - eine Stelle auf dem Wellenleiter, an der konstruktive Interferenz vorliegt und misst dort eine besonders grosse Effektivspannung U_Max = U_Vor + U_Refl. Anschliessend misst man im Abstand λ/4 davon U_Min = U_Vor - U_Refl und berechnet daraus

SWR={\frac {U_{\text{max}}}{U_{\text{min}}}}

Bei sehr kurzen Wellenlängen wird die Messung an einer teilweise offenen Koaxialleitung (engl. slotted line) durchgeführt, sie zeichnet sich durch hohe Genauigkeit aus^[1]^[2]^[3]^[4]. Übersteigt die Wellenlänge einige Meter, ist diese Art der Messung allein wegen der notwendigen Abmessungen problematisch.

Indirekte Messung

Wenn aus Gründen der Abschirmung die Koaxleitung nicht geöffnet werden darf oder die Wellenlänge einige Meter überschreitet, müssen die notwendigen Messwerte indirekt ermittelt werden. Dazu fügt man in den Wellenleiter zwei Richtkoppler ein, die mittels kurzer Drahtstücke aus vor- und rücklaufender Welle Bruchteile der jeweiligen Leistung auskoppeln. Bei sehr hohen Frequenzen im Gigahertzbereich werden diese ausgekoppelten Leistungen unmittelbar kalorisch ohne Gleichrichtung gemessen (siehe Leistungsmessung#Messung_von_Hochfrequenzleistung), es gilt:

{\text{SWR}}={\frac {1+{\sqrt {P_{\text{Refl}}/P_{\text{Vor}}}}}{1-{\sqrt {P_{\text{Refl}}/P_{\text{Vor}}}}}}

Bei Frequenzen um 100 MHz werden die ausgekoppelten Spannungen, die proportional zu U_Vor und U_Refl sind, gleichgerichtet und gemessen. Es gilt:

SWR={\frac {U_{\text{Vor}}+U_{\text{Refl}}}{U_{\text{Vor}}-U_{\text{Refl}}}}

Mit der Wellenlänge müssen auch die Längen der Drahtstücke steigen, damit die ausgekoppelten Spannungen nicht zu klein werden. Das führt bei Frequenzen unter 5 MHz zu so unhandlichen Abmessungen, dass die Drahtstück durch einen Stromwandler (Durchsteckwandler) und zwei einstellbaren Kondensatoren ersetzt werden. Dann ist die gemessene Spannung fast unabhängig von der Wellenlänge.

Nachteilig ist bei indirekten Messungen, dass die Zahl der Fehlerquellen steigt. Bei der Messung des SWR ist deshalb unerlässlich, den Einfluss möglicher Kabelresonanzen zu prüfen, indem das Kabel zwischen Stehwellenmessgerät und Last probeweise um λ/4 verlängert wird.

Strom- und Spannungsverlauf am Wellenleiter

Misst man die Effektivspannungen an unterschiedlichen Stellen entlang einer Doppelleitung bei Gleichstrom oder niederfrequentem Wechselstrom, beobachtet man eine stetige Verringerung in Richtung zum Lastwiderstand, deren Ursache der Spannungsabfall durch den Ohmschen Widerstand der Drähte ist. Bei hoher Frequenz des Wechselstromes und ausreichender Leitungslänge tritt ein neuartiges Phänomen hinzu: Die Spannungswerte erreichen (im Regelfall) in periodischen Abständen Maximalwerte (Ausnahme: Der Lastwiderstand hat präzis den Wert des Wellenwiderstandes). Diese Beobachtung ist die beste Möglichkeit, die Wellenlänge von Hochfrequenz zu messen (Lecher-Leitung) und war vor der Erfindung ausreichend schneller Frequenzzähler die einzige Möglichkeit, indirekt über die Beziehung λ·f = c die Frequenz f zu bestimmen.

Das obere Bild gilt für folgende Annahmen:

Die Kabellänge beträgt genau drei Wellenlängen; das Kabel ist verlustfrei.
Die (reellen) Belastungswiderstände an beiden Enden sind kleiner als der Wellenwiderstand Z des Kabels und werden so gewählt, dass der Reflexionsfaktor ρ = -0,7 ist.
An einem Kabelende speist ein Sender ausreichend Energie ein, damit die Messwerte konstant sind.
Wird der Lastwiderstand unmittelbar am Sender angeschlossen (vernachlässigbare Kabellänge), misst man V_eff = 0,3 V.

Alle Vorgaben werden beispielsweise erfüllt, wenn ein Kabel mit Z = 280 Ω mit R = 50 Ω belastet wird und der Sender (Quellwiderstand = 50 Ω) die Leistung 1,8 mW erzeugt.

Wegen Z > R ist die gemessene Spannung an den Kabelenden minimal; bei Kurzschluss wäre sie Null. Die Messwerte des Stromes sind um 90° phasenverschoben und erreichen genau an den Kabelenden Maximalwerte.

Das untere Bild gilt für folgende Annahmen:

Die Kabellänge beträgt genau drei Wellenlängen.
Die (reellen) Belastungswiderstände an beiden Enden sind größer als der Wellenwiderstand Z des Kabels und werden so gewählt, dass der Reflexionsfaktor ρ = +0,7 ist.
An einem Kabelende speist ein Sender ausreichend Energie ein, damit die Messwerte konstant sind.
Wird der Lastwiderstand unmittelbar am Sender angeschlossen (vernachlässigbare Kabellänge), misst man V_eff = 1,7 V.

Alle Vorgaben werden beispielsweise erfüllt, wenn ein Kabel mit Z = 50 Ω mit R = 280 Ω belastet wird und der Sender (Quellwiderstand = 280 Ω) die Leistung 10,2 mW erzeugt.

Wegen Z < R ist die gemessene Spannung an den Kabelenden maximal; bei offenem Ende wäre sie etwas größer und hängt von der Reaktion des Senders auf die fehlende Last ab. Die Messwerte des Stromes sind um 90° phasenverschoben und erreichen genau an den Kabelenden Minimalwerte.

Das Stehwellenverhältnis hat in beiden Bildern den Wert 1,7/0,3 = 5,67. Sonderfälle:

Falls R = 0 Ω oder R = ∞ Ω, misst man die Minimalwerte 0 V und die Messkurven gleichen Sinus-Halbbögen. Dann spricht man sehr ungenau von "stehenden Wellen", obwohl Wellen niemals stehen können.
Wenn die Abschlusswiderstände ungleich oder sogar komplexwertig sind (also kapazitive oder induktive Anteile enthalten) oder wenn die Kabellänge kein Vielfaches von λ/2 ist, muss die Berechnung des SWR mittels Leitungstheorie erfolgen.
Nur bei exaktem Abschlusswiderstand Z = R sind sowohl Strom- als auch Spannung ortsunabhängig und wären als horizontale Geraden einzuzeichnen.

Physikalische Deutung

Die Ursache der ortsabhängigen Spannung längs eines Wellenleiters sind reflektierte Wellen, die in vom (falsch bemessenen) Lastwiderstand (Antenne) zum Sender zurück laufen. Das lässt sich bei sehr hohen Frequenzen durch Zirkulatoren nachweisen, welche die vorlaufende Wellen kaum dämpfen und nur die rücklaufende Energie auskoppeln. In der Praxis setzt man Zirkulatoren aber selten ein, um SWR = 1 zu erzwingen, weil dadurch wertvolle Sendeleistung vernichtet wird.

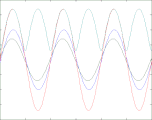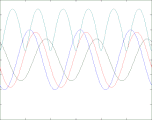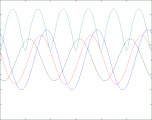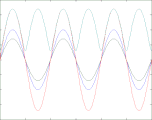
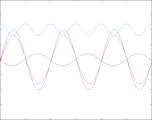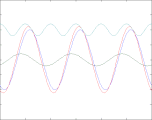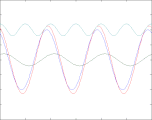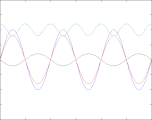
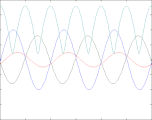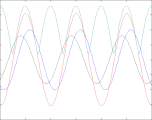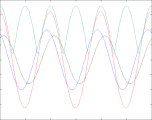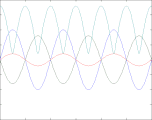
Reflexion einer nach rechts laufenden Welle bei unterschiedlichen Reflexionsfaktoren
Reflexionsfaktor ρ = -0,1
Reflexionsfaktor ρ = -0,7
Reflexionsfaktor ρ = +0,2
Reflexionsfaktor ρ = +0,8

In den vier oben gezeigten Bildern wird der Bruchteil ρ einer in einem Wellenleiter nach rechts laufenden Welle der Amplitude A (blau) reflektiert und läuft mit verringerter Amplitude nach links zurück (grün). Beide überlagern sich und ergeben die rot gezeichnete Welle, die ebenfalls nach rechts läuft und phasenmoduliert ist. Nur diese ist messbar, weil man beispielsweise bei einem Koaxialkabel an jedem Punkt nur eine einzige Spannung messen kann. Abhängig vom Wert des Lastwiderstandes R (am rechten Bildrand) sind zwei Fälle zu unterscheiden:

R < Z: Die reflektierte Welle besitzt entgegengesetzte Phase und verringert deshalb die messbare Spannung an der Last. Bei Kurzschluss ist die Kompensation vollständig, man misst Null. In der Optik entspricht das der Reflexion von Licht an einem optisch dichteren Medium.
R > Z: Die reflektierte Welle besitzt gleiche Phase und vergrößert deshalb die messbare Spannung an der Last. Bei offenem Leitungsende wird die messbare Spannung verdoppelt.

Trägt man die gleichgerichtete Spannung als Funktion des Ortes auf, erhält man die türkis gezeichnete Hüllkurve. Die Hüllkurve hängt nur vom Ort, nicht aber von der Zeit ab, sie ist auch keine physikalische Realität, sondern eine Messkurve, die typischerweise mit einer slotted line ermittelt wird. Wegen ihrer periodischen Struktur wird sie üblicherweise "stehende Welle" genannt, obwohl sie keine physikalische Welle ist und vor allem keine Energie transportiert oder speichert. Die Spannungswerte der Hüllkurve schwanken zwischen den Werten A·(1 + ρ) und A·(1 - ρ).

Man definiert den Reflexionsfaktor ρ

\rho ={\frac {U_{\text{Refl}}}{U_{\text{Vor}}}}={\frac {Z_{\mathrm {Last} }-Z_{\mathrm {Kabel} }}{Z_{\mathrm {Last} }+Z_{\mathrm {Kabel} }}}\qquad |\rho |\leq 1

Dabei bedeuten

Z_Kabel: die Wellenimpedanz der Leitung,
Z_Last: der Eingangswiderstand der am Leitungsende angeschlossenen Schaltung.
U_Vor: die Spannung der hinlaufenden Welle
U_Refl: die Spannung der rücklaufenden Welle

Für Reflexionsfaktor ρ = 0 (SWR = 1) ist die Effektivspannung U = U_Vor entlang des gesamten Wellenleiters gleich groß, es liegt perfekte Leistungsanpassung vor.
Für ρ = 1 (SWR = ∞) schwankt die Effektivspannung ortsabhängig zwischen U_Max = 2·U_Vor und Null. Dann spricht man von einer stehenden Welle.
Für alle anderen Werte von ρ kann man den Spannungsverlauf am Wellenleiter dem nebenstehenden Bild entnehmen. Darin bedeutet V_mot "maximum voltage over time", was im Deutschen etwa U_effektiv entspricht.

Einschwingverhalten bei kontinuierlichen Wellen

Der Satz "Bei einem grossen SWR wird ein hoher Anteil der eingespeisten Leistung am Verbraucher reflektiert und über den Wellenleiter zur Quelle zurück geleitet. Abhängig von deren Impedanz wird dieser Anteil dort absorbiert oder wieder teilweise zum Verbraucher reflektiert" in der Einleitung wird gelegentlich missverstanden und führt dann zur falschen Folgerung, dass bei hohem SWR im Dauerbetrieb nur ein geringer Teil der erzeugten Leistung vom Verbraucher (beispielsweise einer Antenne) absorbiert wird und der Rest verloren ist. Das ist beim Betrieb mit kontinuierlichen Wellen falsch, denn nach einem kurzen Einschwingvorgang gleicht sich die Leistungsbilanz innerhalb weniger Mikrosekunden aus.

Dieses Pendeln von Energie wird an einem Beispiel in Einzelschritten erklärt. Ein Sender (Quellimpedanz = 50 Ω) liefert über eine luftisolierte, verlustarme 300 Ω-Bandleitung der elektrischen Länge n·λ/2 (mit n∈0,1,2,...) Leistung an einen 50 Ω-Lastwiderstand. Gemäß Leitungstheorie findet trotz sehr hohem SWR = 6 eine verlustfreie Übertragung statt, insbesondere wird im Dauerbetrieb die erzeugte Leistung vollständig in der Last "verbraucht". Der Sender kann trotz hohem SWR unmöglich beschädigt werden, weil er wegen der λ/2-Nichttransformation seine Sollimpedanz "sieht".

Im Detail geschieht unmittelbar nach dem Einschalten des Senders folgendes:

Sobald die ersten Wellen die Last erreichen, wird infolge des hohen negativen Reflexionsfaktors ρ = -0,714 der größte Teil der gelieferten Leistung mit entgegengesetzter Phase reflektiert (Kurzschlusscharakteristik).
Erreicht diese reflektierte Leistung den Sender, gilt nun der positive Reflexionsfaktor ρ = +0,714 und der größte Teil dieser Leistung wird gleichphasig in Richtung Last reflektiert (Leerlaufcharakteristik). Der Rest wird zur aktuellen Senderleistung addiert.
Kommt der (am Sender) reflektierte Anteil der (an der Last) reflektierten Leistung erneut an der Last an, addiert er sich zur Senderleistung, weil er zwischenzeitlich einen "Umweg" von 2·n·λ/2 = n·λ zurückgelegt hat und deshalb gleichphasig sein muss. Letztlich erreicht dieser Anteil nach der doppelten Kabellaufzeit die Last und geht nicht verloren.
Die Gesamtleistung an der Last übertrifft deshalb nun für einen kurzen Zeitraum die Senderleistung, der weitere Verlauf geht sinngemäß so weiter, wie unter 1) beschrieben.

Dieses Pendeln von Energie zwischen beiden Kabelenden klingt nach kurzer Zeit ähnlich einer gedämpften Schwingung ab und kann mit einem Transientenrekorder aufgezeichnet werden. Nach Abklingen dieser Transienten fließt die erzeugte Senderleistung vollständig in die Last, obwohl das SWR unverändert hoch ist.

Falls die elektrischen Länge des Kabels kein Vielfaches von λ/2 ist, laufen im Prinzip die gleichen Energie-"Schwingungen" wie beschrieben ab, infolge geänderter Phasenbedingungen dauert der Vorgang jedoch länger.

Bei Signalen ohne kontinuierliche Trägerfrequenz, wie sie in der Datenübertragung, z.B. Ethernet vorkommen, kann kein Einschwingvorgang beobachtet werden. Deshalb kann kein SWR bestimmt werden und als Hilfe zur Fehlerbehebung herangezogen werden.

Refexion von Pulsfolgen

Bei einer Datenübertragung innerhalb der Hauptplatine eines Computers oder beim Ethernet wird eine unregelmässige Folge von Einzelpulsen übertragen, weshalb es kein "Einschwingverhalten" geben kann. Falls das Kabelende nicht mit der korrekten Impedanz belastet ist, wird ein Teil der ankommenden Pulsenergie zum Sender reflektiert. Die Datenempfänger (UART oder USB-Chips) sind immer so gebaut, dass sie die Reduktion der empfangenen Energie problemlos verkraften. Mögliche Probleme werden erst am Sender erzeugt, wobei zwei Fälle zu unterscheiden sind:

Der Quellimpedanz des Senders stimmt mit dem Wellenwiderstand des Kabels überein. Dann wird die Energie des rücklaufenden Impulses hier absorbiert und es gibt keine Störungen der Datenübertragung. Angesichts der geringen Leistung ist keine Überlastung des Senders zu befürchten.
Bei Fehlanpassung wird ein Teil der Impulsenergie mit veringerter Leistung, möglicherweise vertauschter Polarität und vermutlich im falschen Zeitraster zur Last reflektiert und kann dort wie ein (fehlerhaftes) Signal verarbeitet werden.

Bei bidirektionalem Datenverkehr wie USB und Datenbus müssen also beide Kabelenden mit der korrekten Impedanz abgeschlossen werden.

SWR bei besonderen Kabellängen

Die Auswirkungen eines hohen SWR werden häufig überschätzt und können bei gewissen Leitungslängen bedeutungslos sein.

Auch wenn die Leitungslänge viel kürzer als λ ist, kann am Kabelende Fehlanpassung auftreten, wobei eingespeiste Energie reflektiert wird: Alle 230 V-Leitungen (auch Hochspannungsleitungen) sind krass fehlangepasst und trotzdem sehr gut für die Energieübertragung geeignet: Der Quellwiderstand beträgt ≈ 0 Ω, Der Wellenwiderstand der Leitung liegt bei ≈ 300 Ω und der Lastwiderstand schwankt zwischen ≈ 10 Ω und ∞ Ω. Obwohl die Wellenlänge bei 50 Hz so groß ist, dass man das SWR nicht unmittelbar messen kann, gelten auch für diese Frequenz die gleichen physikalische Gesetze wie für Hochfrequenz.

Wenn das Kabel die elektrischen Länge n*λ/2 mit n∈0,1,2,... besitzt, wird der Wert des Lastwiderstandes gemäß Leitungstheorie auch bei beliebigem Wellenwiderstand des Kabels nicht transformiert. Der Sender kann nicht beschädigt werden, weil er seine Sollimpedanz "sieht". Falls das Kabel verlustarm ist, handelt es sich um eine besonders effektive Art der Energieübertragung, die in der Anfangszeit der Funktechnik beliebt war. Einziger Nachteil: Es darf keine nenneswerten Änderungen der Wellenlänge geben.

Beträgt die Länge ein ungerades Vielfaches von λ/4, zeigt das Kabel ausgeprägte Transformationseigenschaften (Resonanztransformator), die mitunter sehr erwünscht sind und vorteilhafte technische Lösungen ermöglichen. Obwohl dabei sehr grosse Reflexionsfaktoren (= grosses SWR!) auftreten, gilt diese Art von HF-Transformator als sehr verlustarm (siehe auch Streifenleitung).

Auswirkungen auf das Kabel

Das Stehwellenverhältnis erlaubt eine Aussage über die Übertragungsverluste im Kabel. Es wird nur durch Kabel und den Wert des Abschlusswiderstandes (z.B. eine Antenne) bestimmt und kann durch keine Maßnahmen am Sender geändert werden.

Die Leistungsverluste entlang des Kabels sind auf zwei Ursachen zurückzuführen:

Die Dielektrische Erwärmung des Isoliermaterials ist proportional zu U². Deshalb steigt der mittlere Energieverlust mit wachsendem Unterschied zwischen U_Max und U_Min. Die größte Verlustwärme im Dielektrikum entsteht an den Stellen des Wellenleiters, an denen U_Max gemessen wird. Bei Luftisolation kann dieser Anteil vernachlässigt werden.
Bei SWR > 1 ist auch die Strombelastung des Kabels ortsabhängig, wobei eine Phasendifferenz von 90° vorliegt: U_Max und I_Min sind am gleichen Ort messbar, ebenso U_Min und I_Max. An allen Orten in der Umgebung von I_Max ist die lokale Erwärmung wegen P = I²·R besonders gross.

SWR = 1. Bei diesem Idealfall tritt keine Reflexion am Kabelende auf, weil der Abschlusswiderstand den korrekten Wert von beispielsweise 50 Ω besitzt. Die in das Kabel eingespeiste Leistung wird vollständig im Abschlusswiderstand verbraucht. Spannungen und Ströme haben überall auf dem Kabel den gleichen Wert, deshalb sind die Energieverluste im Kabel minimal. Daraus folgt aber nicht, dass die Antenne besonders gut abstrahlt; denn wenn man die Antenne durch eine Dummy-Load mit korrektem Widerstand ersetzt, wird trotz SWR = 1 keine Leistung abgestrahlt.
SWR ≈ 2. Ein gutes SWR bedeutet nur, dass zwischen Kabel und Antenne fast Leistungsanpassung vorliegt. Es liefert keine Aussage, ob die Antenne die zugeführte Leistung gut abstrahlt. Spannungen und Ströme unterscheiden sich an unterschiedlichen Stellen des Kabels geringfügig und die Energieverluste sind leicht erhöht.
SWR > 5. Ein schlechtes SWR bedeutet, dass sich die Wellenimpedanz des Kabels stark vom Wert des Abschlusswiderstandes unterscheidet. Spannungen und Ströme unterscheiden sich an unterschiedlichen Stellen des Kabels sehr stark. Im Kabel entstehen unnötig hohe Wärmeverluste. Bei bestimmten Bauarten, beispielsweise der in der Anfangszeit der Funktechnik verwendeten „Hühnerleiter“ (einer zwischen Sender und Antenne frei aufgehängten, luftisolierten Doppelleitung genau definierter Länge), waren die Verluste trotz hohem SWR relativ gering. Grund dafür ist, dass Luft auch bei hohen Spannungen kaum dielektrische Verluste erzeugt.
SWR = ∞. Bei offenem oder kurzgeschlossenen Kabelende tritt vollständige Reflexion der Leistung auf. Das Kabel wirkt wie ein Schwingkreis, dessen Resonanzwellenlängen und -frequenzen nur von der Länge und vom Aufbau des Kabels abhängen (siehe Leitungstheorie#Sonderfall_Kurzschluss).

Auswirkungen auf den Sender

Jeder Sender muss zwischen Endstufe und Antennenbuchse ein selektives Netzwerk aus verlustarmen Kondensatoren und Spulen besitzen, das die Oberwellen ausreichend dämpft. Zugleich ist dieses Netzwerk ein Resonanztransformator, der die notwendige Widerstandstransformation zwischen dem optimalen Belastungswiderstand des aktiven Bauelementes (Röhre oder Transistor) und der Kabelimpedanz herstellt.

Oft kann das Transformationsverhältnis in engen Grenzen variiert werden, was man als Abstimmung bezeichnet. Wenn jedoch die tatsächliche Kabelimpedanz zu stark vom Sollwert (meist 50 Ω) abweicht und zusätzliche induktive oder kapazitive Blindwiderstände aufweist, kann das Netzwerk die tatsächliche Belastungsimpedanz (fehlangepasstes Kabel) nicht mehr in den Toleranzbereich des Endstufentransistors transformieren. Deshalb kann die Maximalspannung oder der Maximalstrom des Transistors überschritten werden (SOAR-Diagramm) und der Verstärker ist zerstört.

Literatur

Otto Zinke, Heinrich Brunswig: Hochfrequenztechnik 1: Hochfrequenzfilter, Leitungen, Antennen. 6. Auflage. Springer, 1999, ISBN 978-3-540-66405-5.

H. Meinke, F. Gundlach, K. Lange, Taschenbuch der Hochfrequenztechnik, Band 2, ISBN = 3540547150

Weblinks

Referenzen

{{SORTIERUNG:Stehwellenverhaltnis}} [[Kategorie:Funktechnik]]

[1] SLOTTED LINE MEASUREMENTS in Englisch

[2] Messverfahren "slotted line" ab Seite 16

[3] HIGH FREQUENCY SLOTTED LINE AND REFLECTOMETER MEASUREMENTS

[4] The Slotted Line

[1]

[2]

[3]

[4]

Benutzer:Ariser/Stehwellenverhältnis Alternativentwurf

Inhaltsverzeichnis

Stehwellenverhältnis von Impulsen und kurzen Wellenpaketen

Stehwellverhältnis von kontinuierlichen Wellen

Unmittelbare Spannungsmessung

Indirekte Messung

Strom- und Spannungsverlauf am Wellenleiter

Physikalische Deutung

Einschwingverhalten bei kontinuierlichen Wellen

Refexion von Pulsfolgen

SWR bei besonderen Kabellängen

Auswirkungen auf das Kabel

Auswirkungen auf den Sender

Literatur

Weblinks

Referenzen

Navigationsmenü

Benutzer:Ariser/Stehwellenverhältnis Alternativentwurf

Stehwellenverhältnis von Impulsen und kurzen Wellenpaketen

Stehwellverhältnis von kontinuierlichen Wellen

Unmittelbare Spannungsmessung

Indirekte Messung

Strom- und Spannungsverlauf am Wellenleiter

Physikalische Deutung

Einschwingverhalten bei kontinuierlichen Wellen

Refexion von Pulsfolgen

SWR bei besonderen Kabellängen

Auswirkungen auf das Kabel

Auswirkungen auf den Sender

Literatur

Weblinks

Referenzen

Navigationsmenü

Suche