Bild (Kategorientheorie)

In der Kategorientheorie ist ein Bild eines Morphismus ein Unterobjekt des Zielobjekts mit einer besonderen Eigenschaft.

Erste Definition

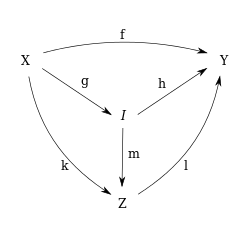
In der Kategorientheorie ist ein Bild eines Morphismus $f\colon X\to Y$ ein Unterobjekt $h\colon I\to Y$ von $Y$, das die folgende universelle Eigenschaft hat:

• Es gibt einen Morphismus $g\colon X\to I$ mit $f=hg$.
• Für jedes Unterobjekt $l\colon Z\to Y$, das obige Eigenschaft erfüllt ($f=lk$), gibt es einen eindeutigen Morphismus $m\colon I\to Z$ mit $k=mg$ und $h=lm$.

Zweite Definition

Ist $f:X\rightarrow Y$ Morphismus in einer Kategorie ${\mathcal {C}}$, so sei ${\mathcal {C}}_{f}$ die Kategorie mit

• Objekten: alle Monomorphismen $h\colon I\rightarrow Y$, so dass es einen Morphismus $g\colon X\rightarrow I$ gibt mit $f=h\circ g$
• Morphismen zwischen Objekten $h_{1}\colon I_{1}\rightarrow Y$ und $h_{2}\colon I_{2}\rightarrow Y$: ${\mathcal {C}}$-Morphismen $m:I_{1}\rightarrow I_{2}$, so dass $h_{1}=h_{2}\circ m$.

Ein Bild von $f$ ist definiert als ein initiales Objekt in ${\mathcal {C}}_{f}$.

Dies ist nichts anderes als eine Umformulierung der universellen Eigenschaft des Bildes.

Kategorien mit Bildern

Man sagt, eine Kategorie habe Bilder, wenn jeder Morphismus ein Bild hat. Die Kategorie der Mengen hat Bilder, denn die Bildmenge einer Abbildung zwischen zwei Mengen ist ein Bild im Sinne der Kategorientheorie. Allgemeiner gilt:

• In einem Topos hat jeder Morphismus $f$ ein Bild $h$ und es gilt sogar $f=h\circ e$ mit einem Epimorphismus $e$.

Kobilder

Das Kobild eines Morphismus $f\colon X\to Y$ ist der duale Begriff: ein Kobild ist ein Quotientenobjekt $g\colon X\to C$ von X, das die folgende universelle Eigenschaft hat:

• Es gibt einen Morphismus $h\colon C\to Y$ mit $f=hg$.
• Für jedes Quotientenobjekt $k\colon X\to Z$, das obige Eigenschaft erfüllt ($f=lk$), gibt es einen eindeutigen Morphismus $m\colon Z\to C$ mit $g=mk$ und $l=hm$.

In Kategorien mit Kern und Kokern ist jeder Kern eines Kokerns von f ein Bild von f, jeder Kokern des Kernes ein Kobild.

In abelschen Kategorien wie den Kategorien der Vektorräume oder abelschen Gruppen stimmen Bild und Kobild überein. In den genannten Kategorien sind sie auch gleich dem mengentheoretischen Bild.