Disheptaeder
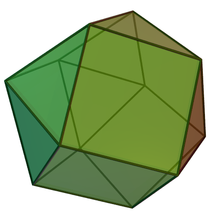

Ein Disheptaeder (auch Antikuboktaeder) ist ein Polyeder, das aus denselben Flächen wie das Kuboktaeder, also denen eines Hexaeders (Kubus) und eines Oktaeders, besteht. In dem Alternativnamen (Anti-Kubooktaeder) stecken entsprechend die Wörter Kubus und Oktaeder. Des Weiteren ist es als Johnson-Körper J27 (Dreiecksdoppelkuppel (verdrehtes Kuboktaeder)) bekannt.
Der Dualkörper des Disheptaeders ist die Voronoi-Zelle einer Kugel in der hexagonal dichtesten Kugelpackung des Typs AB und füllt den Raum als Element einer Parkettierung vollständig, wie auch ihr Gegenstück, das Rhombendodekaeder, das die Voronoi-Zelle für die Kugelpackung Typ ABC und der Dualkörper des Kuboktaeders ist.
Beschreibung
[Bearbeiten | Quelltext bearbeiten]Man erhält ein Disheptaeder aus einem Kuboktaeder durch Schnitt entlang der Ebene, die eine umlaufende Kante zwischen Hexaeder und Oktaederflächen bildet, und anschließende Verdrehung beider Hälften um 180° gegeneinander. Dadurch besitzen im Disheptaeder jeweils 3 Gruppen von je 2 Hexader- und 2 Oktaeder-Flächen eine gemeinsame Kante. Die vorherige Schnittebene wird zu einer Spiegelebene des Körpers.
Mit 14 Flächen (8 gleichseitige Dreiecke und 6 Quadrate), 12 Ecken und 24 Kanten gleicher Länge wird der eulersche Polyedersatz genau wie beim Kuboktaeder erfüllt.
Formeln
[Bearbeiten | Quelltext bearbeiten]
| Größen eines Disheptaeders mit Kantenlänge a | |
|---|---|
| Volumen | |
| Oberflächeninhalt | |
| Umkugelradius | |
| Kantenkugelradius | |
| 3D-Kantenwinkel = 120° |
|
Vorkommen
[Bearbeiten | Quelltext bearbeiten]Das Disheptaeder findet in der Strukturchemie und Kristallographie als Koordinationspolyeder (z. B. in der hexagonal dichtesten Kugelpackung hcp) Verwendung. Die zugehörige Koordinationszahl ist (genau wie beim Kuboktaeder) 12; der Grenzradienquotient ist ebenfalls 1.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Eric W. Weisstein: Disheptaeder. In: MathWorld (englisch).
- beuth-hochschule.de (PDF) S. 7





