Diskussion:Eulersche Phi-Funktion

Links

Eulersche Phi-Funktion (φ)-> wäre schön, das in Sätzen auszugliedern, nicht jeder Leser wird wohl ein WP-Profi sein, um zu bemerken, dass hinter jedem Link ein eigener Artkel steht. --'~'

Teileranzahlfunktion

Der Artikel Teileranzahlfunktion behandelt ebenfalls die Eulersche Phifunktion. Der Name "Eulersche Phifunktion" dürfte jedoch gebräuchlicher sein. --Ich hab hunga 22:28, 21. Jul 2006 (CEST)

Nein & nein.--Gunther 15:52, 27. Jul 2006 (CEST)

Ich nehme alles zurück, und behaupte das Gegenteil ;). Es muss die Hitze sein... --Ich hab hunga 09:07, 28. Jul 2006 (CEST)

Fehler in Darstellung

>Wenn zwei ganze Zahlen a und m ≥ 2 teilerfremd sind, gilt: > m \mid a^{\varphi(m)-1}, >oder anders formuliert: > a^{\varphi(m)} \equiv 1 \pmod m Muss nicht das minus 1 von a hoch phi von m minus eins wieder aus dem Exponenten heraus?

Fourier-Transformation

Die explizierte Gleichung stimmt NICHT!!! (nicht signierter Beitrag von 217.87.149.68 (Diskussion) 12:30, 25. Feb. 2016 (CET))

Was stimmt denn nicht? Wenn ich richtig sehe, steht die Formel doch so in der Einleitung der angegebenen Quelle. -- HilberTraum (d, m) 17:43, 25. Feb. 2016 (CET)

"zwischen"

In der Definition "Sie gibt für jede natürliche Zahl n an, wieviele natürliche Zahlen zwischen 1 und n zu ihr teilerfremd sind." wird das Wort "zwischen" in zwei verschiedenen, einander widersprechenden Bedeutungen verwendet (inklusive untere Grenze 1, exklusive obere Grenze n).

Beide Grenzen sind eingeschlossen, allerdings ist $n$ nur für $n=1$ teilerfremd zu sich selbst. Es gilt dementsprechend $\varphi (1)=1$, wäre $n$ ausgeschlossen, müsste der Wert 0 sein.

Danke für die prompte und klare Antwort. Soll man die anderslautende Formulierung "Die Eulersche φ-Funktion ordnet jeder natürlichen Zahl n die Anzahl der zu n teilerfremden Zahlen, die kleiner als n sind, zu." im Artikel Teilerfremdheit korrigieren? DirkDe 22:15, 5. Sep 2006 (CEST)

So, wie das dort steht, weiß man sowieso nicht, ob die 0 erlaubt ist, und mit der 0 ist's wieder richtig. Vom Standpunkt eines Algebraikers wäre der "richtige" zu testende Bereich die Menge der Restklassen oder alternativ das übliche Vertretersystem $0\leq ?\leq n-1$. Mach's so, wie es Dir einleuchtend erscheint.--Gunther 22:24, 5. Sep 2006 (CEST)

11..22

Hat das nen Grund, den ich nicht durchschaue, dass die Zahlen 11..22 aus der Tabelle entfernt wurden? Gruß, -- zOiDberg ^{(Δ | Α & Ω)} 16:06, 14. Sep 2006 (CEST)

Damit wäre die Tabelle zu breit geworden.--Gunther 16:07, 14. Sep 2006 (CEST)

Breit ist relativ ... auf dem PDA ist auch diese Tabelle zu breit (mutmaße ich). Eventuell zwei Zeilen oder Liste vertikal und dafür am rechten Rand? Ich halte letzeres für einen schönen Kompromiss. Gruß, -- zOiDberg ^{(Δ | Α & Ω)} 16:09, 14. Sep 2006 (CEST)

Die weiteren Werte erklären nicht mehr, die allgemeine Berechnungsformel steht ja unten.--Gunther 16:12, 14. Sep 2006 (CEST)

Ja da hast Du eigentlich auch wieder Recht. Naja als Nachschlagetabelle wäre es aber dennoch hilfreich (ja mir ist klar dass Wikipedia eine Enzyklopädie ist). -- zOiDberg ^{(Δ | Α & Ω)} 16:23, 14. Sep 2006 (CEST)

Fehler in der Darstellung von phi(n)

Man Macht das Produkt nicht über alle Teiler, sondern über alle Primzahlen... nachrechnen!

Nachlesen! $p|n$ bedeutet gerade: alle Primzahlen $p$, die $n$ teilen. Diese Notation ist üblich. --Stefan Birkner 17:49, 13. Feb. 2007 (CET)

Def von phi(n)

Was macht der Betragsstrich in [1]? Meiner Meinung nach ist der ueberfluessig. [1] http://upload.wikimedia.org/math/d/e/8/de81ef9fe241b134e3651f99d3178480.png

Das sind keine Betragsstriche sonder die Elementanzahlfunktion. Die Formel lautet:

Phi von n ist gleich der Anzahl der Elemente der Menge $\{1\leq a\leq n\,|\,\operatorname {ggT} (a,n)=1\}$

--Stefan Birkner 08:01, 7. Apr. 2008 (CEST)

Potenz von Primzahlen

Ich bin ja kein Experte auf dem Gebiet, aber müßte es in der vierten Zeile dieses Absatzes nicht heißen "Das sind $k-1$ Zahlen, die nicht teilerfremd zu $p^{k}$ sind." statt "Das sind $p^{k-1}$ Zahlen, die nicht teilerfremd zu $p^{k}$ sind."? (nicht signierter Beitrag von Q5616417 (Diskussion | Beiträge) )

Das $p^{k-1}$ war richtig, jedoch sind die Zahlen darüber nicht in Ordnung gewesen. Das hab ich mal schnell korrigiert. Gruß, --Tolentino 12:19, 12. Sep. 2008 (CEST)

Zahlen, die nicht Wert der Phi-Funktion sein können

In der Liste besonderer Zahlen steht als Eigenschaft der 3, dass sie die kleinste Zahl sei, die nicht Wert der Phi-Funktion auftritt. Das klingt so, als gäbe es da noch mehr. Welche sind das denn? Gibt es unendlich viele davon? --RokerHRO 21:25, 23. Apr. 2009 (CEST)

Offenbar kann keine ungerade Primzahl Funktionswert der Phi-Funktion sein. Denn:

1. φ(1) = 1
2. Jede ungerade Zahl n > 1 hat ungeraden Primteiler, der liefert in der Produktdarstellung von φ(n) einen geraden Faktor.
3. Das Doppelte einer ungeraden Zahl hat denselben φ-Wert wie diese.
4. Das 2²-fache, 2³-fache, 2⁴- … jeder ungeraden Zahl hat einen φ-Wert, der durch 2¹, 2², 2³ … teilbar ist, also einen geraden.

Also gibt es unendlich viele natürliche Zahlen, die nicht Funktionswert der Phi-Funktion sind. Man findet unschwer weitere, etwa von der Gestalt 2p mit p prim, 2p+1 nicht prim. -- Silvicola Diskussion Silvicola 05:23, 24. Apr. 2009 (CEST)

Hm, das wertet diese "besondere Eigenschaft" der Zahl 3 ja schon irgendwie ab, weils gar nichts sooo besonderes mehr ist, oder? :-/ --RokerHRO 23:17, 25. Apr. 2009 (CEST)

Allgemeiner: Keine ungerade Zahl außer der 1 ist Funktionswert der Phi-Funktion. Denn ungerades n hat stets zumindest eine ungerade Primzahlpotenz $p^{k}$ als Faktor, φ(n) dementsprechend das gerade $(p-1)p^{k-1}$, womit φ(n) in diesen Falle gerade ist. Die dann allein als Urbildkandidaten ungerader Funktionswerte noch verbleibenden Zweierpotenzen liefern aber für Exponenten ≥ 2 alle gerade Zahlen, 2 und 1 jedoch 1. -- Silvicola Diskussion Silvicola 07:51, 26. Apr. 2009 (CEST)

Multiplikativ?

Bin ich gerade doof oder so?

Für Phi(2*9) = Phi(18) = Phi(2) * Phi(9) = 1 * 6 = 6 // Hier funktioniert das

Aber was ist mit:

Phi(2*4) = Phi(8) = Phi(2) * Phi(4) = 1 * 2 != 4 // Widerspruch

Phi(3*3) = Phi(9) = Phi(3) * Phi(3) = 2 * 2 != 6 // Widerspruch

...

-- 193.197.55.175 15:14, 20. Jul. 2010 (CEST)

 Lesen bildet. "Nur für teilerfremde(!) Zahlen m und n gilt Phi(n*m) = Phi(n) * Phi(m)

Abschätzung

In der Darstellung unter Beispiele sind die Geraden x-1 und 4x/15 zur Abschätzung der phi-Funktion nach oben und unten eingezeichnet. Sollte man das unter dem Abschnitt Abschätzung nicht auch diskutieren/herleiten? (nicht signierter Beitrag von 91.33.124.217 (Diskussion) 17:30, 21. Mai 2011 (CEST))

Die Gerade $y=x-1$ ist klar, und die andere irreführend, weil diese Grenze eigentlich nicht gilt: $\varphi (210)=48\,<\,{\frac {4\cdot 210}{15}}=56$. Keine Ahnung, warum die untere Gerade eingezeichnet ist. --Daniel5Ko 18:26, 21. Mai 2011 (CEST)

Falsche Grafik

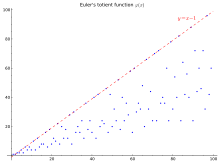
Die Datei EulerPhi100.svg, Darstellung rechts, ist mathematisch falsch. Definitionsmenge sind die natürlichen Zahlen N und nicht die reellen Zahlen R. Es gibt daher keine Zwischenwerte für nichtganze Argumente. Daher besteht der Graph aus einer Punktfolge und nicht aus einer Linie. Die geradlinigen Verbindungen sind nicht definiert. Ich habe die Datei daher aus dem Artikel genommen. ÅñŧóñŜûŝî (Ð) 14:35, 13. Mai 2012 (CEST)

(n,j)=1

Unter 'Weitere Beziehungen' wird das Symbol (n,j)=1 verwendet, aber nicht erklaert. Was ist das? (nicht signierter Beitrag von 92.75.83.117 (Diskussion) 14:43, 2. Jan. 2014 (CET))

(i,j) ist eine Kurzschreibweise für ggT(i,j), den größten gemeinsamen Teiler von i und j. Ich habe es soeben im Artikel präzisiert.--Franz 16:49, 2. Jan. 2014 (CET)

Komplexe Funktionsdefinition

Auf Wikidata gibt es unter "Formel" eine deutlich einfacher ausehende Formel (Zumindest für mich). Ist die Formel auf Wikidata falsch? Wenn nein warum steht die nicht auch hier? (nicht signierter Beitrag von Worthefre (Diskussion | Beiträge) 1. Februar 2018, 21:08:49)

Ich nehme mal an, Du meinst, das im Abschnitt Allgemeine Berechnungsformel zu findende

$\varphi (n)=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right)$

sei einfacher als die Definition

$\varphi (n):={\Big |}\{a\in \mathbb {N} \mid 1\leq a\leq n\land \operatorname {ggT} (a,n)=1\}{\Big |}$

aus der Einleitung (wo sich auch eine Verbalisierung findet, deren Beachtung die Definition vermutlich weniger „komplex“ erscheinen läßt als ein erster Blick auf die formalisierte Version). Bedenke auch den Unterschied zwischen der Definition einer Funktion und einem (nicht eindeutig bestimmten, in manchen Fällen auch gar nicht exitierenden) Funktionsterm, den man manchmal vorteilhafter zur Berechnung eines konkreten Funktionswertes verwenden kann als die Definition.

Gruß, Franz 00:32, 2. Feb. 2018 (CET) P. S.: Lies Dir bitte mal unsere Hilfeseite zum Signieren von Diskussionsbeiträgen durch.

Nontotients

Man sollte noch einen Abschnitt zum Wertebereich anlegen, ähnlich zu en:Nontotient. (Muß nicht so ausführlich sein.)—Godung Gwahag (Diskussion) 18:51, 7. Aug. 2018 (CEST)

Primzahlen

Original: "Da eine Primzahl p nur durch 1 und sich selbst teilbar ist, ist sie zu den Zahlen 1 bis p−1 teilerfremd. Weil sie größer als 1 ist, ist sie außerdem nicht zu sich selbst teilerfremd. Es gilt daher

   φ ( p ) = p − 1"

Wäre so etwas nicht verständlicher: "Da alle Primzahlen p nur durch 1 und sich selbst teilbar sind, gilt:

   φ ( p ) = p − 1

( Anmerkung/Hinweis: Für p und auch sonst alle Zahlen gilt, dass sie durch sich selbst teilbar sind und somit nicht in die Zählmenge für φ fallen. Die 1 (für die φ ( p ) = p − 1 nicht aufginge), ist zwar für φ zulässig, zählt aber per Definition nicht zu den Primzahlen, somit gilt die Formal für alle p )" Oder habe ich da Inhaltlich etwas falsch verstanden? Ansonsten wäre schon ein Satz ohne doppelte Verneinung: "...ist sie außerdem ein Teiler für sich selbst." besser. Vorschläge bitte. --Fredric (Diskussion) 20:33, 5. Aug. 2020 (CEST)

aktuelle Seitensperre

Da ich zu schnell gespeichert hatte, vorsorglich auch hier der Hinweis: Bitte nicht über Zusammenfassungszeile austauschen, sondern über diese Diskussionsseite. Bei Einigung gerne auf Entsperrwünsche melden. Freundl. Grüsse --Nordprinz (Diskussion) 17:57, 26. Apr. 2022 (CEST)

So, wie es jetzt im Artikel steht ("phi ist für n>1 die Anzahl der zu n teilerfremden positiven Reste modulo n") ist es zwar richtig, aber die Einschränkung "positive" könnte man zur Vereinfachung weglassen. Für $n>1$ spielt es keine Rolle, ob man die 0 einschließt, denn sie ist nicht teilerfremd zu n. Außerdem würde ich auch die Einschränkung n>1 weglassen und einfach schreiben:

$\varphi (n)$ ist die Anzahl der zu $n$ teilerfremden Reste modulo $n$.

Das kann man als Beschreibung einer Eigenschaft oder als alternative Definition auffassen. Es gilt auch für $n=1$, da 0 teilerfremd zu 1 ist (die 1 ist zu allen Zahlen teilerfremd). Wegen mir muss man nicht unbedingt hinzufügen, dass für n > 1 der Funktionswert im Bereich $1\leq \varphi (n)<n$ liegt, aber man kann es tun.--Megatherium (Diskussion) 19:08, 26. Apr. 2022 (CEST)

Definition

Es gibt zwei sinnvolle (und gleichbedeutende) Definitionen der Phi-Funktion $\varphi \colon \mathbb {N} ^{+}\to \mathbb {N} ^{+}$:

$\varphi (n)\;:=\;{\Big |}\{a\in \mathbb {N} \,\mid \,1\leq a\leq n\land \operatorname {ggT} (a,n)=1\}{\Big |}$

$\varphi (n)\;:=\;{\Big |}\{a\in \mathbb {N} \,\mid \,0\leq a<n\land \operatorname {ggT} (a,n)=1\}{\Big |}$

--Megatherium (Diskussion) 21:40, 19. Nov. 2022 (CET)

Änderung 228130588 von Daniel5Ko

Das "Ausmisten" eines Wikipedia-Artikels mit der schnöden Begründung "trivial, redundant" sollte unterbleiben. Die Streichung einer durchaus sinnvollen Formel, die die darüberstehende Mengendefinition anschaulicher machen kann, und die schon lange an diesem Platz steht, ist nicht sinnvoll. Die Worte "trivial" und "redundant" wurden hier massiv umgedeutet. Die Formel ist weder trivial noch redundant. Außerdem wäre absolute Redundanzfreiheit in keiner Weise ein Qualitätsmerkmal eines Artikels, sondern die Transformation in eine Maschinensprache. Deshalb habe ich die Änderung rückgängig gemacht. --2003:EA:5F3D:5E00:EDE3:7213:5310:4CB 18:20, 23. Nov. 2022 (CET)

Man könnte natürlich überall, wo über Kardinalitäten von endlichen Mengen gesprochen wird, $|M|$ durch $\sum _{m\in M}1$ ergänzen. Nur, wozu? Wie man zählt, sollten die meisten Menschen ja wissen. Anschaulicher wird m.E. gar nichts, sondern es werden eher Fragen aufgeworfen wie "Warum steht denn das hier?", "Übersehe ich einen subtilen Unterschied?", "Warum steht analoges nicht in Teileranzahlfunktion?" etc., die sich einfach erübrigen, wenn der Satz nicht hier steht.

Gegen Redundanz an sich habe ich übrigens nichts (daher auch "Trivial redundant." im Änderungskommentar und nicht "Redundant."). Ganz im Gegenteil. Redundanz ist nicht zuletzt zur Fehlererkennung nützlich. Beispiele sind in dem Sinn gute Redundanzen: Falls jemand eine Definition (und sonst nichts) verkehrt ändert, kann danach anhand vorhandener Beispiele durch jedermann festgestellt werden, dass etwas am Artikel nicht stimmt. Zumindest, wenn die Beispiele gut genug sind.

Ach ja, und falls jetzt jemand fragt, ob Beispiele nicht viel trivialere Redundanzen sind: Mag sein, aber: Die Beispiele haben idealerweise speziell mit dem Artikelgegenstand zu tun. $|\{a\in \mathbb {N} \,\mid \,1\leq a\leq n\land \operatorname {ggT} (a,n)=1\}|=\sum \limits _{\overset {1\leq a\leq n}{\operatorname {ggT} (a,n)=1}}1$ kann man dagegen beweisen, ohne genau zu wissen, was ggT, $\mathbb {N}$ usw. sind. --Daniel5Ko (Diskussion) 22:56, 23. Nov. 2022 (CET)

"Wie man zählt, sollten die meisten Menschen ja wissen."

Genau wieder so ein elitärer Satz, wie die (Pseudo-)Begründung "trivial redundant" für das Streichen einer Formel, die sich irgendein Wikipedia-Mitautor irgendwann einmal zur (seiner Meinung nach) Verbesserung der Verständlichkeit ausgedacht hat, und die auch lange Zeit akzeptiert worden ist. Wikipedia ist aber kein elitäres Projekt, etwa als Ersatz für ein nicht selbst geschriebenes Mathe-Buch.

Um nur einmal anzufangen aufzuzählen, wie wenig das Urteil "trivial redundant" zutrifft:

- Nicht unbedingt "die meisten Menschen" kennen das Mächtigkeitssymbol (|...|) der Mengenlehre.

- Die eigentliche Definitionsformel in dem Artikel ist eine Mengendefinition, während die nun ausradierte Formel eine (sicher nicht sehr anspruchsvolle) Berechnungsvorschrift darstellt.

- Einen substanziellen Begriff "Trivialität" findet man sicher in der formalen Logik. In vielen anderen Bereichen wird jeweils konkret definiert, was unter "triviale/r ..." zu verstehen sei.

- ... (hier gibt es wohl noch genügend Raum zur Fortsetzung) --2003:EA:5F1A:5400:6C5D:474:CC6C:60C8 22:44, 25. Nov. 2022 (CET)

Du argumentierst gegen irrelevantes. Mein Änderungskommentar ist egal. Die Frage ist, ob der fragliche Text im Artikel sein soll, oder nicht. Meine Ansicht ist: Wer $|\{?\}|$ lesen kann, kann auch $\sum _{?}1$ lesen (und umgekehrt). Ohne sehr sehr deutlich darauf hinzuweisen, dass es sich um eine triviale Umformulierung handelt, stiftet es daher mehr Verwirrung als es hilft, beides im Artikel zu haben.

Ich empfinde es im Übrigen als sehr elitär (um das mal zurückzuwerfen), die Leser für Blödiane zu halten, die man mit "viel hilft viel" abspeisen kann. --Daniel5Ko (Diskussion) 02:26, 28. Nov. 2022 (CET)