Diskussion:L-Funktion

Bildlegende

Kodieren nicht die verschiedenen Farben verschiedene Funktionswerte zu den komplexen Argumenten (die durch die Position im Koordinatenkreuz kodiert sind)? Vgl. Wiki-Eintrag zur Riemannschen Zeta-Funktion. (nicht signierter Beitrag von 77.180.81.240 (Diskussion) 16:23, 14. Mai 2016 (CEST))

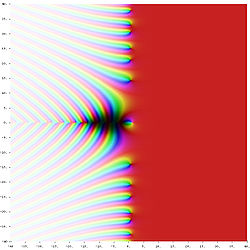
Verschiedene Farben kodieren die Funktionswerte noch nicht vollständig, sondern nur deren Argumente (also den Winkel gemessen gegen die positive, reelle Achse). Die noch fehlende Information über den Absolutbetrag des Funktionswertes wird über die Farbschattierung der Farbe kodiert: hell und blass erscheinende Farben gehören zu Funktionswerten mit großem Absolutbetrag (die unendliche Polstelle der Riemannschen Zeta-Funktion in z=1 wird durch einen rein weißen Punkt kodiert), während dunkel und intensiv erscheinende Farben einen Absolutbetrag nahe Null repräsentieren (insbesondere die Nullstellen der Riemannschen Zeta-Funktion mit Realteil = 0.5 sind als schwarze Punkte im Schaubild erkennbar). Aus dem Schaubild "Verwendete Kodierung" kann man die Darstellung der einzelnen, komplexen Funktionswerte vollständig ablesen:

• 
  Riemannsche Zeta-Funktion
• 
  Verwendete Kodierung

Mathematisch ausgedrückt steht man bei Schaubildern von komplexwertigen Funktionen komplexer Argumente vor der Schwierigkeit, insgesamt vier reelle Dimensionen (zwei reelle Dimensionen für die komplexen Funktionsargumente und zwei reelle Dimensionen für die komplexen Funktionswerte) in einem zweidimensionalen Schaubild zu kodieren. Hier gibt es natürlich mehrere Möglichkeiten. Das abgebildete Schaubild der Riemannschen Zeta-Funtion repräsentiert die zwei reellen Dimensionen der Funktionsargumente durch ihre Lage in der komplexen Ebene, einem zweidimensionalen Vektorraum über den reellen Zahlen. So weit, so natürlich. Damit sind aber auch schon alle zur Verfügung stehenden Dimensionen des Schaubilds aufgebraucht. Die zwei reellen Dimensionen der komplexen Funktionswerte werden dann einerseits durch die Farbe und andererseits durch deren Farbschattierung kodiert. Chrgue (Diskussion) 18:22, 15. Mai 2016 (CEST)

Gamma-Faktoren zu Hecke-L-Funktionen

Hallo, insbesondere @Chrgue:,

ich habe mein Problem mit der Definition der Gammafaktoren $\Gamma _{\mathbb {R} }$ und $\Gamma _{\mathbb {C} }$, da sich die Literatur hier widersprüchlich äußert. Habe bereits in der angegebenen Quelle Popescu und co. nachgesehen; weite Teile sind daraus ja übernommen worden. Dort wird zum Beispiel für eine reelle Stelle $v$ mit zugehörigem (unitären) Charakter $t\mapsto |t|^{iq}(t/|t|)^{m}$, wir setzen $s_{0}:=iq$

$L(\chi _{v},s)=\pi ^{-(s+iq+m)/2}\Gamma \left({\frac {s+iq+m}{2}}\right)$

definiert. In Daniel Bumps Automorphic Forms and Representations auf den Seiten 77/78 wird jedoch für den Charakter $t\mapsto \operatorname {sgn}(t)^{\varepsilon _{j}}|t|^{\nu _{j}}$ explizit der Faktor

$\Gamma \left({\frac {s-\nu _{j}+\varepsilon _{j}}{2}}\right)$

benutzt. Und auch bei Neukirchs Algebraic number theory findet ein Vorzeichenwechsel statt, siehe S. 497. Nun reden beide über unitäre Charaktere, aber auch im allgemeinen Setting scheint die obere Formel, schenkt man Bump und Neukirch Glauben (und der Vorzeichenwechsel macht auch Beweistechnisch Sinn!) falsch zu sein. Kennt jemand das richtige Resultat? Danke!

Beste Grüße, --Googolplexian1221 16:29, 14. Nov. 2019 (CET)

Hallo, insbesondere @Googolplexian1221:,

vielleicht entgeht mir der entscheidende Punkt deines Beitrags, aber ich habe nochmal in drei Quellen geprüft, wie dort jeweils die Gammafaktoren $\Gamma _{\mathbb {R} }$ und $\Gamma _{\mathbb {C} }$ definiert sind, nämlich in

1) David Rohrlich: Root Numbers. In: Popescu et al. (Hrsg.): Arithmetic of L-Functions. 2011, Part III, Lecture 1, Abschnitt 1, S. 358;

2) Neukirch: Algebraische Zahlentheorie. Kapitel 7, Paragraph 12, 1992, S. 558; und

3) Ehud de Shalit: Artin L-Functions. In: Bernstein, Gelbart (Hrsg.): An Introduction to the Langlands Program. 2004, Kapitel 4, Abschnitt 4.1, S. 80

Und sie sind in allen drei Quellen gleich definiert: $\Gamma _{\mathbb {R} }(z):=\pi ^{-z/2}\Gamma (z/2)$ und $\Gamma _{\mathbb {C} }(z):=2\cdot (2\pi )^{-z}\Gamma (z)$.

Auch LMFDB, die Internet-Datenbank für L-Funktionen und Modulformen, verwendet genau diese Definitionen; siehe https://www.lmfdb.org/knowledge/show/lfunction.gamma_factor.

Aber der springende Punkt deines Beitrags ist eigentlich ein anderer, oder?

Grüße, Chrgue (Diskussion) 17:59, 6. Dez. 2019 (CET)

Hallo @Chrgue:, danke für die Antwort! Ja, ich hatte mich etwas umständlich ausgedrückt. Es besteht Klarheit um die Gamma-Faktoren an sich, jedoch nicht, auf welche Weise die Exponenten der "infinity-part" Charaktere dort eingesetzt werden. Während bei Rohrlich das Vorzeichen vor $s_{0}$ positiv ist, ist es bei Neukirch und Bump negativ, also in deren Schreibweise $-iq$ wenn der Charakter durch $t\mapsto |t|^{iq}(t/|t|)^{m}$ gegeben ist. Nun gilt aber sicherlich im Allgemeinen

$\Gamma \left({\frac {s-iq+m}{2}}\right)\not =\Gamma \left({\frac {s+iq+m}{2}}\right)$

d.h. der finale Gamma-Faktor ist sehr "sensibel" gegenüber der eindeutigen Wahl dieser Exponenten. Vielleicht verstehe ich die Notation nicht, aber aus meiner Sicht müsste es bei Rohrlich $\Gamma _{\mathbb {K} }(s-s_{0}+\varepsilon )$ statt $\Gamma _{\mathbb {K} }(s+s_{0}+\varepsilon )$ (mit $\varepsilon =m,|m|/2$ je nach $\mathbb {K} \in \{\mathbb {R} ,\mathbb {C} \}$) sein. Ich hoffe, mein Punkt ist einigermaßen klar. Vielen Dank!

Beste Grüße, --Googolplexian1221 09:23, 17. Dez. 2019 (CET)

Hallo,

es tut mir leid, @Googolplexian1221: aber eine wirklich "scharfe" Antwort auf deine Frage erfordert mehr Zeit, als ich, ehrlich gesagt, in diese Plus-Minus-Vorzeichenangelegenheit investieren möchte. Vermutlich verwendet ein Autor bei der Definition der Charaktere ein Plus, und der andere ein Minus, bzw. schreibt Dinge in den Zähler, die anderswo im Nenner stehen, und das überträgt sich dann bis hin zu den Gamma-Faktoren - so jedenfalls meine Vermutung. Ich habe in der Weihnachtszeit über eine Stunde recherchiert. Da die Formeln, so wie sie im Artikel stehen, konsistent und mehrfach belegt sind, verzeihe mir bitte, wenn ich hier in der Diskussion deine Frage nicht abschließend beantworte.

--Chrgue (Diskussion) 16:31, 17. Jan. 2020 (CET)

Ist kein Problem, vielen Dank trotzdem für deine Mühe! :-) -- Googolplexian (Diskussion) 13:24, 25. Mär. 2020 (CET)