Diskussion:Nutation (Astronomie)

Nutation vs Aberration

Habe "interessanterweise" durch "zufälligerweise" ersetzt. Tatsächlich ist solch eine Zusammentreffen phänomenologisch erst mal interessant, denn es deutet auf eine gemeinsame Ursache hin. Darauf macht das Wort "interessanterweise" aufmerksam, was aber in die Irre führt, weil die Aberration reine Optik ist. Gruß Thomas (ohne Datum signierter Beitrag von 85.180.64.84 (Diskussion) 01:14, 7. Mai 2007 (CEST))

trefflich analysiert, danke -- W!B: 03:02, 7. Mai 2007 (CEST)

Nutation vs Präzession

Es sollte vielleicht erwähnt werden, dass die Verwendung des Begriffs "Nutation" in diesem Artikel (und der Astronomie im Allgemeinen) nicht deckungsgleich ist mit dem Begriff "Nutation" im physikalischen Sinn (siehe Nutation (Physik)). Die hier erwähnte "Nutation" ist physikalisch eine Präzession (durch äußere Drehmomente verursacht). Dass die Erde auch noch eine echte (also physikalische) Nutation ausführt, wird hier leider gar nicht erwähnt. Diese Bewegung hat eine Periode von < 2 Jahren, eine Amplitude von < 1 Winkelsekunde und wird nicht durch äußere Drehmomente verursacht. Diese Bewegung wäre also auch noch vorhanden, wenn die Erde alleine im Universum wäre. Im englischen Artikel ist die echte Nutation zumindest kurz erwähnt, allerdings wird dort ebenfalls keine klare Unterscheidung getroffen. --Catskineater 03:42, 19. Sep. 2008 (CEST)

Sehe ich exakt genau so. Die doppelte Verwendung von Nutation halte ich im Prinzip für "gefährlich", gerde da die astronomische Nutation einen Präzession beschreibt, die mit der physikalischen Nutation verwechselt werden kann. Da du den Unterschied zwischen physikalischer und astronomischer Nutation genauso siehst wie ich, habe ich den Artikel mal soweit es mir möglich war angepasst. --GammaRay 01:46, 4. Mär. 2009 (CET)

Sieht gut aus. Deine Änderungen machen es etwas klarer. Catskineater 00:45, 3. Aug. 2009 (CEST)

Berechnungsgrundlagen

Der Großteil des Artikels wird von den Berechnungsgrundlagen eingenommen. Kaum jemand wird das benötigen. Der Laie kapierts eh nicht und jemand der diese Berechnungen durchführen muss, muss eh auf Bücher zurückgreifen. Dazu trägt der Abschnitt nicht zum verständnis bei. Man KANN natürlich nennen wie die Berechnungen durchzuführen sind, aber ohne diese großen Tabellen. Ne Idee wäre, dass man erklärt dass es viele große Terme gibt die man betrachten muss, dahinter noch ein Verweis auf z.B. das Buch "Astronomical Algorithms" oder ähnliche in welchem diese dann beschrieben sind. Also meine Meinung: Abschnitt komplett neu schreiben/ersetzen. -- 84.152.157.245 15:28, 21. Apr. 2012 (CEST)

Wer auch immer die Berechnungen und Beispiele hinzugefügt hat: Sie haben mir sehr geholfen, bitte auf jeden Fall beibehalten. (nicht signierter Beitrag von 79.140.120.141 (Diskussion) 18:02, 4. Feb. 2021 (CET))

Scale?

(Entschuldigen Sie mir Bitte für schreiben in Englisch.) The scale on the image says that the nutation varies between +/- 18 archseconds. This is twice the actual value. (If I had tried German this would have been the result: Der Schale bei das Bild sagt das der Nutation variert zwischen +/- 18 Bogensekunde. Das ist zweimal die faktische Verte. At least a nice try!) Episcophagus (Diskussion) 23:22, 26. Dez. 2018 (CET)

The figure is correct. It shows both components of nutation, namely nutation in obliquity (Δε) in red and nutation in longitude (Δψ) in blue. The first term with a period of 18.6 years has an amplitude of 9.2″ in obliquity and 17.2″ in longitude. --BurghardRichter (Diskussion) 23:57, 26. Dez. 2018 (CET)

@BurghardRichter: The amplitude in obliquity is in reality +/- 9.2" (see for instance nutation in Encyclopaedia Britannica or page 603 in A Concise History of the Theories of Tides By Martin Ekman or page 470 in Nutations of the earth by P.M. Mathews and I.I. Shapiro.). The scale on the image says +/-18" (or something like that - it goes from +20" to -20" - LOOK AT THE SCALE AT THE LEFT IN THE DIAGRAM! - Excuse me for shouting!). The amplitude in longitude is about +/-7". The scale gives twice that amount. Give a reference for your claim! Episcophagus (Diskussion) 00:53, 27. Dez. 2018 (CET)

@BurghardRichter: Even the article says so: "Die Amplitude dieser Komponente beträgt ±9,2″ rechtwinklig zur Ekliptik und ±6,8″ parallel zur Ekliptik. Weitere Komponenten der Nutation haben Amplituden unter 1″ und kürzere Perioden." Episcophagus (Diskussion) 01:00, 27. Dez. 2018 (CET)

The ordinate scale of the diagram extends from −20″ up to +20″. The nutation in obliquity Δε is indicated by the red curve, and you can see that it varies approximately between −9″ and +9″, according to its major-term amplitude of 9.2″. The nutation in longitude Δψ is indicated by the blue curve; it varies approximately between −17″ and +17″, according to its major-term amplitude of 17.2″. So, what is your problem?

Please be aware that Δψ is the periodical variation of the ecliptical longitude ψ of the earth rotation axis. It is measured on the ecliptic plane and therefore refers to the projection of the rotation axis onto the ecliptic. Each nutation term describes an elliptical motion of the pole of the rotation axis on the celestial sphere. The semi-major and semi-minor axes of the ellipse are the amplitude of Δε perpendicular to the ecliptic and the amplitude of Δψ sin ε parallel to the ecliptic, where ε = 23° 26′ is the mean obliquity of the ecliptic (that is the orthogonal complement of the mean ecliptical latitude of the rotation axis). Thus for the major term of nutation (with 18.6-year period), the semi-major and semi-minor axes of the ellipse are equal to the amplitude of Δε = 9.2″ and the amplitude of Δψ sin ε = 6.84″, respectively. The factor sin ε is due to the projection onto the ecliptic, where Δψ is actually measured. --BurghardRichter (Diskussion) 02:26, 27. Dez. 2018 (CET)

@BurghardRichter: Thanks for clarifying! The sentence Die Amplitude dieser Komponente beträgt ±9,2″ rechtwinklig zur Ekliptik und ±6,8″ parallel zur Ekliptik. in the introduction is however confusing and may I recommend that you add something like ..., which corresponds to ±17.2" in ecliptical longitude. (a figure that is never mentioned in the article!) - or, perhaps better, start with ecliptical coordinates, and then "convert" ±17.2" in longitude to which corresponds to ±6.8" along the great circle perpendicular to the meridian. When the article later introduces Δε and Δψ one (at least I did) automatically links the values given (which I recognized) with Δε and Δψ - or rather the curves in the diagram (which shows the principal, semiannual and forthnightly nutations - so I directly applied the curve with the larger amplitude to ±9.2" and the smaller to ±6.8"), so please add a small explanation to the diagram/text and stress that it is the difference in eclipitcal longitude measured along the parallel at 66.5° (and not the actual angular difference measured on a great circle perpendicular to the meridian that is given in the introduction) in diagram and formulas. It might help the next reader? Also the rechtwinklig zur Ekliptik is confusing, because it is the angular difference between the axis and the normal of the ecliptical plane (or between the equatotial and ecliptical planes) and is actually "measured at an angle" of 23,5°, and not 90°, to the plane. Also the expression parallel zur Ekliptik is confusing even though the "tangent" to the arc at the "point" it is measured is "parallel" to the ecliptic. I find it confusing when the article starts with one system of measurement, and then, without actual notice, switches to another. Or? Regards. Episcophagus (Diskussion) 13:05, 27. Dez. 2018 (CET)

@Episcophagus: As to the difference between the two numbers 6.8″ and 9.2″, you can compare it with distances between neighbouring points on the earth: When you walk in north-south direction, the distance corresponds directly to the geographical latitude difference Δφ. However, when you walk in east-west direction, the distance does not directly correspond to the geographical longitude difference Δλ but to Δλ cos φ, where λ and φ are geographical longitude and latitude, respectively. That is due to the fact that two meridians approach each other when you are walking from the equator towards the north or south pole, whereas their geographical longitude difference is always constant. In both cases, we have spherical coordinates longitude and latitude, on the earth or on the celstial sphere and with respect to different coordinate systems, an equatorial terrestrial one and an elliptical celestial one, respectively. It is typical for such spherical coordinates that the corresponding metric factors are 1 for latitude and cosine of the latitude for longitude. The reason that in the case of astronomical nutation we have sin ε (instead of cosine) is that ε is not the ecliptical latitude of the rotation axis, but its orthogonal complement, namely the obliquity of the ecliptic, that is the angle between the rotation axis and the normal vector of the ecliptic or, equivalently, between the planes of the equator and the ecliptic.

I know that this article has a lot of shortcomings. However, in the introduction, I think we should only give a geometrical description of the motions of the earth rotation axis, without any reference to ecliptical coordinates; that would be too sophisticated for the introduction. 6.8″ and 9.2″ are the amplitudes of the actual motion in two perpendicular directions. There is no motion with an amplitude of 17.2″. This number is involved only by the (arbitrary) choice of the coordinate system for the numerical description.

The formulations “rechtwinklig zur Ekliptik” (perpendicualar to the ecliptic) and “parallel zur Ekliptik” (parallel to the ecliptic) are meant in the sense that the one component of motion is measured along a great circle perpendicular to the ecliptic and the other one is measured along a small circle parallel to the ecliptic. Of course, we are here not speaking about motions in three-dimensional space, but on the celestial sphere.

I have strong criticisms of this article. It is absolutely intolerable that it presents numerical values of the nutation parameters Δψ and Δε and even complicated formulae for calculating them according to the nutation theory of 1980, without giving any explanation of the geometrical meaning of these parameters or of the other parameters occurring in the formulae. --BurghardRichter (Diskussion) 23:47, 1. Jan. 2019 (CET)

@BurghardRichter: I agree with your opinions. It is very confusingly written and it made me misunderstand quite a lot. In my opinion the text should be more focused on telling how the nutation varies and the reasons to those variations. I made an image of the 6.8"/9.2" ellipse that I use in an article I am trying to write on Swedish Wikipedia (I see from your user-page that you understand Swedish) and discuss the principal, semi-annual and semi-monthly nutations, giving amplitudes and periods, but no unmotivated (and partly obsolete, as there is IAU 2000A with 1375 correctional terms) formulas. I use "ecliptical coordinates" (and try to explain obliquity) and write something like »... and 17.2" in longitude. Seen from the center of the Earth this gives an ellipse with semi-major axis 9.2" and semi-minor axis 6.8" (the latter figure obtained by multiplying Δψ with sin ε).« when explaining the 7"/9" ellipse. The article is not finished yet, and I have some diffuse rubbish left to write on an elastic mantle and liquid core, as well as some kind of blurry stuff on polar wandering (and, of course, reformulating most of what I already have written a dozen times). There should also be a short history chapter. Regards. Episcophagus (Diskussion) 10:17, 2. Jan. 2019 (CET)

Also, instead of "perpendicular to the ecliptic", I would prefer "parallel to the projection of the earth's axis on the ecliptical plane", as it excludes the infinitely many other directions in the plane that is perpendicular to the ecliptic in a given point (for instance a direction normal to the ecliptical plane, which is the only direction that is perpendicular to every part of the ecliptic). Episcophagus (Diskussion) 10:42, 2. Jan. 2019 (CET)

Ja, der schwedische Artikel ist viel besser. --Rainald62 (Diskussion) 16:14, 5. Jan. 2019 (CET)

Falsches Bild

Präzession und Nutation eines starren Körpers

Nutationselipse der Erdachse für den Zeitraum von 2015 bis 2033

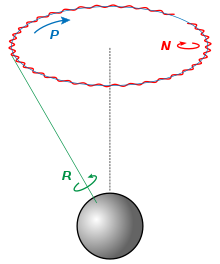
Das obere Bild rechts ist im Moment als Illustration zu diesem Artikel eingebunden. Es zeigt die Präzession und Nutation eines starren Körpers, nicht die Nutation eines Planeten, die hier in diesem Artikel gemeint ist. Wie oben schon mehrfach festgestellt, ist die Nutation von Planeten der schnelle Anteil der Präzession. Außerdem sieht die Spur der momentanen Drehachse weder für die Nutation starrer Körper noch für die astronomische Nutation wie ein Sinus aus. Bei der astronomischen Nutation ergibt sich üblicherweise eine Folge von Schlaufen. Siehe das untere Bild der berechneten Nutation der Erdachse für den Zeitraum von 2015 bis 2033. Ich werde daher die beiden Bilder austauschen.---<)kmk(>- (Diskussion) 23:17, 15. Jul. 2019 (CEST)

Nein, das stimmt so nicht; die Präzession ist der säkulare Anteil, die Nutation der (kurz-)periodische Anteil der Richtungsänderung der Erdachse relativ zu einem raumfesten System. Bitte lass das bisherige Bild stehen! Es veranschaulicht als Prinzipskizze sehr gut das Zusammenwirken von Präzession und Nutation. Mit starrem Körper hat das nichts zu tun. Der Unterschied zwischen einer starren Erde und der realen deformierbaren Erde zeigt sich nicht in der Nutation, insbesondere nicht in deren längerperiodischen Anteilen, sondern in der Polbewegung (Chandlersche statt Eulersche Periode und unregelmässige Anteile) oder entsprechend in den tagesperiodischen Anteilen der Nutation.

Das von dir vorgeschlagene Bild ist keine Prinzipskizze, sondern zeigt die reale Nutation für den genannten Zeitraum; zu erkennen sind der 18,6-Jahres-Term sowie der Halbjahres- und der Halbmonatsterm. Die sehen bei der Annahme einer starren Erde (etwa Woolardsches Nutationsmodell) exakt genauso aus. Der Nachteil dieses Bildes ist, dass es die Nutation isoliert, also ohne die Präzession, zeigt. Daher halte ich es für den Anfang des Artikels für ungeeignet. Es ist besser weiter hinten angeordnet, wo die Hauptterme der Nutation explizit aufgeführt sind. --BurghardRichter (Diskussion) 00:54, 16. Jul. 2019 (CEST)

Nutation der Länge und Schiefe

Meiner Meinung nach kann die Nutationselipse ruhig an den Anfang des Artikels, allerdings bin auch ich gegen eine Entfernung des oberen Bildes, da es zum Verständnis erforderlich ist. Ich halte aber noch eine weitere Skizze für sinnvoll, aus der das Auseinanderziehen der Nutationselipse infolge der Präzession erkennbar wird (werde ich bei Gelegenheit anfertigen).

Bei der Nutationselipse fällt mir auf, dass die beiden Jahreszahlen falsch eingezeichnet sein müssen. Nicht 2016 (unten) ist das Jahr mit der max. negativen Schiefe von -9,2", sondern 2020 / 2021. Die Jahre 2033 und 2015 müssten korrekterweise auf der linken Seite von der Bildmitte aus eingezeichnet werden. Zumindest wenn die Daten aus dem unteren Bild „Nutation der Länge und Schiefe“ stimmen (was ich nicht überprüft habe). Oder liege ich da falsch? --Helko Peters (Diskussion) 06:20, 22. Jun. 2024 (CEST)