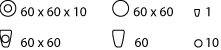Diskussion:Sexagesimalsystem
Archiv bis 2007
[Quelltext bearbeiten]Die Annahme, dass das sumerische Sexagesimalsystem auf der 60 beruht, ist eine nicht korrekte Auffassung. Vielmehr muss man davon ausgehen, dass eine wechselnde Multiplikationsfolge mit den Zahlen 6 bzw. 10 die Grundlage bildet. Ergänzt man dieses System mit den heutigen Erkenntnissen der Mathematik, ergeben die ersten 10 Teilergebnisse folgendes Bild:
6° x 0 = 0;
10° x 1 = 1;
6 x 1 = 6;
10 x 6 = 60;
6 x 60 = 360;
10 x 360 = 3.600;
6 x 3.600 = 21.600;
10 x 21.600 = 216.000;
6 x 216.000 = 1.296.000;
10 x 1.296.000 = 12.960.000;
... x ... = ...
von Benutzer Hores (ich denke so sollte das aussehen--WerWil 20:02, 19. Feb. 2007 (CET))
Die Begründung das System eigne sich besonders gut z. B. zum erstellen von Fahrplänen ist zielmich drollig, angesichts der im Text gemachten Aussagen es stamme von den alten Babyloniern und würde heute noch bei Winkelberechungen verwendet. Daraus folgt, dass die Babylonier Fahrpläne hatten? Denn heute werden Systeme auf Basis 60 ja anscheinend dafür nicht verwendet.--WerWil 20:02, 19. Feb. 2007 (CET)
Die Begründung, dass es heute noch verwendet wird, ist, dass 60 viele Teiler hat. Die Fahrpläne sind nur Beispiele. Die vielen Teiler haben auch in anderen Bereichen Vorteile. Ein Viertel ist im Hexagesimalsystem 15 von 60. Im Dezimalsystem: 2,5 von 10, also ein Bruch.--84.178.11.187 17:30, 3. Jun. 2007 (CEST)
- Sehr richtig IP, man sollte seinen Grips schon erstmal anstrengen @WerWil, dass die Sumerer ein noch komplizierteres (raffinierteres) System aus der Kombination von 6 und 10 hatten @Hores widerspricht ja nicht der Aussage, dass die Basis dennoch 60 ist. Denn das ist sie 60 = 6 x 10. Soviel ich weiß, ist das bei Hexa- oder Sexagesimalsystemen immer so. Aber die Sumerer kann man aufnehmen.
- Aber warum gab es nur 20 Zahlzeichen? es ist doch kein Vigesimalsystem?--Löschfix 01:27, 27. Jun. 2007 (CEST)
- 20 Zahlzeichen? Meinst Du nun Einzelzahlzeichen oder Zahlen, die in Zahleinzelzeichen ausgedrückt wurden? Direkte Zahlzeichen waren ja nur : 1,10 und die Veränderung dieser Zeichen in der optischen Größe für die nächsten Einheiten. Gruss NebMaatRe 12:47, 7. Okt. 2007 (CEST)
Ausbau
[Quelltext bearbeiten]Da noch sehr viele Informationen und Beispiele im Artikel fehlen, sollte er ausgebaut werden. Habe damit mal angefangen. Andere haben bestimmt auch noch viel Wissenswertes. --NebMaatRe 17:35, 7. Okt. 2007 (CEST)
Zählen
[Quelltext bearbeiten]Es ist praktischer mit der linken Hand zu zaehlen, weil dann die Rechte noch frei ist. Zudem ist die Richtung beliebig, je nachdem ob in dreier oder vierergruppen gezaehlt wird. Als Kind habe ich jedenfalls gelernt, dass der Daumen auf der Zeigefingersprize die 1 ist, und auf der Wurzel des kleinen Fingers die 12. Also genau andersrum als im Beispiel beschrieben. 91.66.12.150 21:40, 31. Mär. 2009 (CEST)
Fehler?
[Quelltext bearbeiten]Ich kenne mich damit nicht aus, aber sollte es bei dem ersten Beispiel der "Weitere Zahlenbeispiele:" nicht
"![]()
![]() = 660" sondern "
= 660" sondern "![]()
![]() = 601" heißen?
= 601" heißen?
- Danke für den Hinweis. Auch 601 wäre falsch, eher 11 (dann aber zusammen). Auch das nebenstehende Beispiel war nicht nachvollziehbar. Beide wurden nun gelöscht. --NebMaatRe 11:24, 18. Dez. 2007 (CET)
Bitte Nachweise
[Quelltext bearbeiten]Bitte die Nachweise und links zu der interessanten Geschichte mit den Wolfsknochen.... Es klingt so mystisch--Brakbekl 21:34, 1. Mär. 2008 (CET)
- Nachweis eingefügt, 1.Kapitel im Buch von "Zeitreise...." --NebMaatRe 22:13, 1. Mär. 2008 (CET)
Dividieren
[Quelltext bearbeiten]Was ueber dividieren erzaehlt wird, ist ziemlich unklar.82.75.63.115 18:39, 25. Mär. 2008 (CET)
- 1.Schritt: Umdenken in 60er Basis, 2.Schritt Die Hälfte von 60 ist 30, also wurde 1/2 mit der Zahl 30 ausgedrückt; 1/12 = Zahl 5 etc. (5x12=60). 3.Schritt Rechnen mit "Brüchen" 1/4 (= 15) + 1/12 (= 5) = 4/12 = 1/3 = 20 im Sexagesimalsystem.--NebMaatRe 19:09, 25. Mär. 2008 (CET)
Frühsumerische Ziffern (um 3000 v. Chr.)
[Quelltext bearbeiten]In "Mathematik Maße und Gewichte in der Antike" von O.A.W. Dilke (Reclam Verlag) ISBN 3-15-008687 wird das Sexagesimalsystem in Babylonischer Verwendung mMn recht anschaulich illustriert.
Ich habe, mit Verwendung des oben aufgeführten Werkes als Quelle dienend, eine Illustration der Ziffern 1,10,60,60x10,60x60 und 60x60x10 entworfen, das möglicherweise zu einer besseren Veranschaulichung des Sexagesimalsystems[[1]] beitragen könnte. So hoffe ich zumindest.
Falls keine Verwendung für die Grafik gefunden wird, habe ich es zumindest angemerkt oder eine weitere Quelle genannt, die vielleicht von Nutzen ist.
Wenn erwünscht, wäre ich bereit, eine schönere/bessere Version dieser Ziffern anzufertigen, die diesen Artikel diesbezüglich ergänzen würden. Gruß--PoorPoor 16:01, 25. Jun. 2008 (CEST)
- Das wäre nicht schlecht. Allerdings müssten die Zeichen um 90° (gegen den Uhrzeigersinn) gedreht werden, zumindest sind sie so im Buch von Vogel (S. 18) gezeichnet. Gruss --RPI 16:37, 5. Mär. 2009 (CET)
Schreibweise mit modernen Ziffern
[Quelltext bearbeiten]Hi, auf en:Sexagesimal wird bei der Notation im Sexagesimalsystem mit modernen Ziffern zur Abgrenzung der Zweiergruppen voneinander der Doppelpunkt statt dem Komma verwendet. Sprich, die Zahl 90 wird dann 1:30 geschrieben und nicht wie hier 1,30. Die Schreibweise mit Doppelpunkt scheint mir sinnvoll zu sein, da der Leser seit der Erfindung der Digitaluhren damit vertraut ist, sexagesimale Zahlen so abzulesen (meist sogar ohne darüber nachzudenken.) --GluonBall 15:27, 22. Jul. 2008 (CEST)
- Gegen die Schreibweise mit Doppelpunkt sprechen zwei Gründe:
- 1. Die hier im deutschen Artikel verwendete Schreibweise mit Kommata und Semikolon ist wissenschaftlicher Standard, den man auch auf den Seiten findet, deren Links im englischen Artikel angegeben sind.
- 2. Digitaluhren zeigen kein reines Sexagesimalsystem, weil ein Tag nur 24 Stunden und keine 60 Stunden hat. Hat man noch kleinere Einheiten als Sekunden (z.B. bei Stoppuhren), dann werden diese kleineren Einheiten ausserdem nach dem Dezimalsystem (10tel, 100tel Sekunden usw.) gebildet. Die Digitale Anzeige benutzt zu dem üblicher Weise zwei Stellen, auch bei einstelligen Zahlen: z.B. 16:01 und nicht 16:1 (bei Wikipedia ist das auch so).
- Gruss --RPI 16:31, 5. Mär. 2009 (CET)
Abstrakte Formelverwendung
[Quelltext bearbeiten]Im Artikel steht unter "Der Satz des Pythagoras in Babylon":
Die Babylonier kannten die abstrakte Formelverwendung nicht; ihre mathematischen Kenntnisse wurden in der Praxis umgesetzt, ohne für wiederkehrende Rechenoperationen allgemeine Grundsätze zu notieren.
Das ist so nicht richtig. Richtig ist, dass die entdeckten babylonischen mathematischen Texte fast ausschließlich aus Tabellenwerken und Übungsaufgaben bestehen. Es gibt jedoch noch - wenn auch sehr selten - allgemein formulierte Lösungsverfahren in Worten ohne Zahlen, z.B. auf der altbabylonischen Keilschrifttafel IM 52301, auf der die allgemeine Berechnung der Quadratwurzel einer beliebigen Zahl angegeben ist (K. Vogel: Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier. Schroedel, Hannover und Schöningh, Paderborn 1959. S. 34f, 5.). Ebenso wird auf der Keilschrifttafel BM 34568 aus der Seleukidenzeit (K. Vogel. S. 68, d) β)) u.a. die allgemeine Formel für die Berechnung der Diagonalen eines Rechtecks in Worten ohne Zahlen beschrieben. --RPI 18:52, 4. Feb. 2009 (CET)
Der Satz des Pythagoras in Babylon
[Quelltext bearbeiten]Im Artikel werden unter "Der Satz des Pythagoras in Babylon" die Zahlen als ganzzahlig angegeben, was sicher falsch ist: Da 1 GAR ca. 6 m entspricht, müsste ein Balken von 30 GAR 180 m lang sein! Selbst wenn man kleinere Längeneinheiten als GAR zu Grunde legen würde (K. Vogel. S. 20) wie gi (Rohr/Rute = 1/2 GAR), kùš (Elle = 1/12 GAR) oder šu-si (Finger/Zoll = 1/360 GAR), käme man auf Längen von 30 gi ≈ 90 m, 30 kùš ≈ 15 m oder 30 šu-si ≈ 0,5 m, so dass 30 gi noch immer viel zu lang sind, auch 30 kùš sind zwar möglich aber immer noch zu groß und 30 šu-si nicht nur zu kurz sondern auch gleich 1 kùš, was dann wohl angegeben worden wäre. Die in der wissenschaftlichen Fachliteratur (H. Gericke: Mathematik in Antike und Orient, Berlin 1984, S. 33.) angegebenen Maße von 0;30 GAR ≈ 3 m usw. treffen den Sachverhalt sehr viel besser, so dass diese auch im Artikel genannt werden sollten. --RPI 11:16, 9. Feb. 2009 (CET)
- Der Satz des Pythagoras ist rein geometrisch und hat deshalb mit dem Sexagesimalsystem an sich nichts zu tun, er ist also deshalb hier im Artikel fehl am Platz. Es genügt, wenn seine babylonische Verwendung im Artikel zum Satz des Pythagoras steht. --RPI 22:40, 3. Mär. 2009 (CET)
Babylonische Ziffern
[Quelltext bearbeiten]Babylonische Ziffern löschdisk, nachtrag --W!B: 16:39, 16. Sep. 2009 (CEST)
Weblinks
[Quelltext bearbeiten]folgender Link funktioniert momentan nicht: Dr. Christoph Grandt: Das Babylonische Sexagesimalsystem. (PDF- Datei) Sollte sich das nicht ändern, bitte löschen, danke.-- 95.89.102.108 20:57, 28. Aug. 2010 (CEST)
- geht wieder. -- seth 21:03, 29. Aug. 2010 (CEST)
Zählen großer Zahlen
[Quelltext bearbeiten]Das Zählen mit zwei händen ist nicht bei 72 ausgeschöpft sondern bei 144(12 x 12). Man geht nachdem bis 12 gezählt wurde mit der linken Hand ein Fingerglied weiter und erhällt so ein Gros. 93.218.105.148 22:11, 3. Sep. 2010 (CEST)
- wenn man binaer zaehlt, kann man mit zehn fingern auch einfach bis 1023 zaehlen, aber der komplette abschnitt ist ohnehin besser im artikel Zählen aufgehoben. ich wuerde ihn demnaechst dorthinverschieben, wenn keiner einwaende hat und mir niemand zuvorkommt. -- seth 10:16, 4. Sep. 2010 (CEST)
Die Zahlzeichen: das Leerzeichen
[Quelltext bearbeiten]Um Missverständnisse auszuschließen habe ich die Bedeutung des Leerzeichens präzisiert, das zwar den Stellenwert einer Null hatte, aber nicht die Zahl Null repräsentierte. --RPI 12:30, 1. Sep. 2011 (CEST)
Astronomie
[Quelltext bearbeiten]Die längliche Abhandlung zu den Schaltmonaten scheint mir in Bezug auf das Sexagesimalsystem nur von geringem Interesse. Nötigenfalls reicht wohl ein Verweis auf http://de.wikipedia.org/wiki/Schaltmonat#.C3.84gyptischer_Kalender. Wichtiger ist sicher ein Bezug zur Zahl 360, der gegenwärtig leider untergeht: Aufgrund ihrer vielen Primfaktoren sind 360 Tage günstig in gleichlange Untereinheiten zu zerlegen. So lässt sich die Jahreslänge von 365,2422 Tagen praktisch annähern.--Laufe42 (Diskussion) 08:16, 22. Jun. 2013 (CEST)
Das Sexagesimalsystem (oder Hexagesimalsystem) ist ein Stellenwertsystem und "Hexagesi" steht nicht im Wörterbuch
[Quelltext bearbeiten]Kann mir bitte einer mal sagen, woher das Wort "Hexagesimalsystem" kommt, ich finde es in keinem deutschen Wörterbuch, dort geht es immer nur zum "Hexadezimalsystem". Lieben Dank. (nicht signierter Beitrag von Fritzjetzt (Diskussion | Beiträge) 15:41, 9. Okt. 2013 (CEST))
- Hexagesimal kenne ich auch nicht. Das scheint mir eine seltene Variante zu sein, vielleicht eine hyperkorrekte Spontanbildung – es ist eine merkwürdige Mischung aus lateinisch sexagesimus und dem altgriechischen hexa-. Allerdings ist auch schon das hexadezimal, was diese Variante inspiriert zu haben scheint, schon eine merkwürdige Hybridbildung. --Florian Blaschke (Diskussion) 00:25, 6. Dez. 2013 (CET)
Sexagesimalsystem, Zahlzeichen
[Quelltext bearbeiten]Die Graphik zeigt ein Dezimalsystem und kein Sexagesimalsystem.--87.122.94.6 16:37, 20. Nov. 2019 (CET)