Belastung (Physik)
Als Belastung – kurz: Last – werden alle äußeren Kraftgrößen (Kräfte und Momente) und eingeprägte Verformungen (Verschiebungen, temperaturbedingte und durch Zwängungen verursachte Längenänderungen u. a.) bezeichnet, die auf ein Bauteil wirken. Im Kontext der Baustatik wird auch der Begriff Einwirkung verwendet.
Entsprechend dem newtonschen Reaktionsprinzip führen Belastungen, sofern sie sich nicht gegenseitig aufheben, zu einer Beanspruchung im Bauteil. Diese kann als Spannung ausgedrückt werden und ruft je nach Steifigkeit entsprechende Gestaltänderungen (Deformationen) hervor. Grundlegend ist die Belastungsrechnung in der gesamten Technik für die Ermittlung von Grenzlasten, bei denen die im Bauteil auftretenden Spannungen zum Bruch oder anderem Versagen führen, und damit zur Festlegung von notwendiger Tragfähigkeit und zulässiger Nutzlast.
Grundlagen
[Bearbeiten | Quelltext bearbeiten]Entsprechend der verschiedenen Arten von Belastungen werden unterschiedliche physikalische Größen zur Definition von Lasten verwendet, welche zusätzlich als Funktionen von Ort und Zeit angegeben werden können. Zeitlich konstante Lasten werden als statische Lasten bezeichnet, wobei weiter zwischen beweglichen Lasten (Wanderlasten) und Dauerlasten unterschieden wird, letztere greifen immer im selben Punkt an. Dynamische Lasten sind hingegen zeitabhängig.
Im Falle von Kräften werden außerdem auf Raumdimensionen bezogene Größen verwendet[1], wobei sich folgende Einteilung ergibt:
| Bezeichnung | übliches
Formelzeichen |
Dimension | Beispiel |
|---|---|---|---|
| Punktlast oder Einzellast | Kraft | Auflast einer Stütze, Gewichtskraft einer Punktmasse | |
| Streckenlast oder Linienlast | Kraft pro Länge | linienförmig aufgebrachte Last bei einem Balken | |
| Flächenlast | Kraft pro Fläche | Wasserdruck auf eine Oberfläche | |
| Volumenlast | , (Wichte) | Kraft pro Volumen | Eigengewicht des Bauteils, häufig in Form einer Wichte |
Auch Momente werden gelegentlich auf die Länge bezogen, beispielsweise bei einem Streckentorsionsmoment[2].
Eine konstante (nicht von , oder abhängige) Last wird als gleichförmig verteilte Last oder Gleichlast bezeichnet. Im eindimensionalen Fall wird hierfür auch der Begriff Gleichstreckenlast verwendet.
Zeitliche Änderungen (dynamische Last)
[Bearbeiten | Quelltext bearbeiten]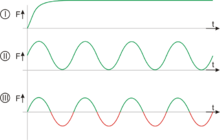
Im Falle zeitlich veränderlicher Lasten werden folgende Fälle unterschieden:
- Belastungsfall I: Ruhende bzw. statische Belastung – Belastung steigt nur bis zu einem bestimmten Punkt und bleibt ab dort konstant. (Beispiel: Last hängt am Seil.)
- Belastungsfall II: Schwellende Belastung – Die Kraft schwankt (ist jedoch stets ungleich 0). → Unterspannung ist bei schwellender Belastung immer gleich null, weil sich das Werkstück immer in die Ausgangslage zurückbewegt.
- Belastungsfall III: Schwingende bzw. wechselnde Belastung – Die Kraft schwingt von Minus nach Plus und von Plus nach Minus usw. (Beispiel: Pleuel).
Die Belastungsfälle II und III können weiter beschrieben werden, indem von einem praktisch häufigen periodischen (zumeist sinusförmigen) zeitlichen Belastungsverlauf ausgegangen wird. Ausschlaggebend sind dann das obere bzw. untere Maximum der Belastungskurve. Ihr Verhältnis, auch Belastungsverhältnis genannt, ist der R-Wert
- .
Wenn entsprechend der Vorzeichenkonvention Druckspannungen mit negativem und Zugspannungen mit positivem Vorzeichen versehen werden, können für R folgende Spezialfälle unterschieden werden, die jeweils eigene Bezeichnungen tragen:
| R-Wert | Bezeichnung | ||
|---|---|---|---|
| Zugschwellbelastung (Fall I) | |||
| Druckschwellbelastung (Fall II) | |||
| Wechselbelastung (Fall III) |
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik. 1: Statik / Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall. 13., aktualisierte Auflage. Springer, Berlin, Heidelberg 2016, ISBN 978-3-662-49471-4. S. 11
- ↑ Technische Mechanik. 2: Elastostatik / Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall. 13., aktualisierte Auflage. Springer Vieweg, Berlin, Heidelberg 2017, ISBN 978-3-662-53678-0. S. 174
















