Elliott-Wellen

Die Elliott-Wellen sind ein Mittel der technischen Analyse zur Vorhersage von Trends in Finanzmärkten.

Allgemeines

Die Theorie wurde 1938 von dem US-Amerikaner Ralph Nelson Elliott entwickelt. Seine „Wellen“ stellen eine deterministische Abfolge dar, die auf der Fibonacci-Folge und dem Goldenen Schnitt beruht. Elliott versuchte damit, psychologische Aspekte des Käuferverhaltens zu berücksichtigen. Bedeutend zur Weiterentwicklung und Verbreitung der Elliott-Wellen-Theorie haben die US-Amerikaner Alfred Frost und Robert Prechter beigetragen. Die Elliott-Wellen-Theorie ist insbesondere eine Analyse massenpsychologisch bedingter Marktbewegungen des Aktienmarktes. Wie andere Instrumente der technischen Analyse ist auch die Elliott-Wellen-Theorie umstritten. Wissenschaftliche Untersuchungen haben überwiegend ergeben, dass eine Vorhersage von Kursentwicklungen nicht möglich ist.

Wellen-Theorie

Grundlegendes Konzept

Aus dem Aufsatz „The Basis of the Wave Principle“ von R. N. Elliott (1940)

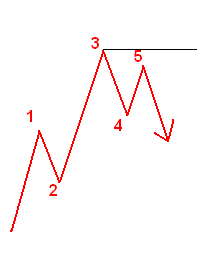
Die Wellentheorie von Elliott basiert auf der Annahme, dass die kollektiven Gefühle der Investoren zwischen Optimismus und Pessimismus schwanken. Diese Schwankungen erzeugen Muster. Elliotts Theorie besagt, dass Preise innerhalb eines Trends in fünf und drei Wellen schwanken. Die nebenstehende Grafik zeigt das Grundprinzip. Innerhalb des Trends sind die Wellen, die im obersten Graphen mit 1, 3, und 5 bezeichnet sind, so genannte Antriebs- oder Motiv-Wellen. Die Wellen 2 und 4 sind Korrekturwellen. Die Antriebswellen gliedern sich ihrerseits wieder in fünf Wellen und die Korrekturwellen in drei Wellen auf. Auf diese Weise entsteht der fraktale Charakter.

Die Aufgabe der Wellen-Theorie ist es, das Verhalten des Marktes zu beschreiben und nur sekundär Aussagen über die zukünftige Entwicklung zu machen.

Bezeichnungen

Da die Wellen aufgrund ihrer fraktalen Natur unterschiedliche Zeiträume umfassen, hat Elliott diesen unterschiedlichen Zeiträumen besondere Bezeichnungen gegeben. Die standardisierte Bezeichnung der Wellen erfolgt folgendermaßen:

Name	Zeitraum	Antriebswellen	Korrekturwellen
Grand supercycle	Jahrhunderte	eingekreiste große römische Zahlen	eingekreiste kleine Buchstaben
Supercycle	Jahrzehnte (40–70 Jahre)	geklammerte große römische Zahlen, z. B. (I), (II)	geklammerte kleine Buchstaben, z. B. (a), (b)
Cycle	ein Jahr bis Dekaden	allein stehende große römische Zahlen, z. B. I, II	allein stehende kleine Buchstaben, z. B. a, b
Primary	Monate bis Jahre	eingekreiste indische Ziffern	eingekreiste große Buchstaben
Intermediate	Wochen oder Monate	geklammerte indische Ziffern, z. B. (1), (2)	geklammerte große Buchstaben, z. B. (A), (B)
Minor	Wochen	indische Ziffern, z. B. 1, 2	große Buchstaben, z. B. A, B
Minute	Tage	eingekreiste kleine römische Zahlen	eingekreiste kleine Buchstaben
Minuette	Stunden	geklammerte kleine römische Zahlen, z. B. (i), (ii)	geklammerte kleine Buchstaben, z. B. (a), (b)
Subminuette	Minuten	kleine römische Zahlen, z. B. i, ii	kleine Buchstaben, z. B. a, b

Motive-Wellen

Zu den Motive-Wellen gehören die Impuls-Wellen sowie die Diagonalen-Dreiecke.

Impulswellen

Eine Impulswelle bewegt sich in fünf Wellen. Hierbei stellen die Wellen 1, 3 und 5 ihrerseits Motive-Wellen dar, sowie die Wellen 2 und 4 Korrekturwellen.

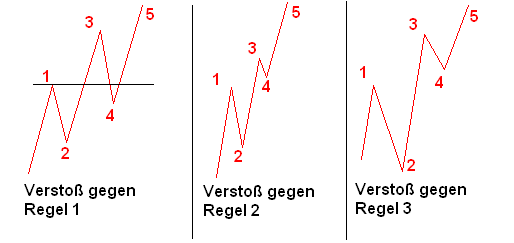
Für die Identifizierung von Impulswellen gelten folgende Regeln:

1. Die Welle 4 darf sich nicht mit der Welle 1 überschneiden.
2. Die Welle 3 ist nie die kürzeste.
3. Die Welle 2 darf nicht unter den Startpunkt von Welle 1 laufen.

Verstößt eine Chartformation gegen diese Regeln, handelt es sich nicht um eine gültige Zählung für eine Impulswelle. In diesem Fall ist die Zählweise zu korrigieren oder es liegt eine andere Formation vor.

Die meisten Impulswellen enthalten Erweiterungen (weitere Unterteilungen), die meist – aber nicht immer – in der Welle 3 stattfinden, sodass sich die Anzahl der Wellen auf neun erhöht:

Gelegentlich kann es vorkommen, dass die Welle 5 verkürzt ist, hierbei überschreitet die Welle 5 nicht die Welle 3:

Diagonale Dreiecke

Die diagonalen Dreiecke bewegen sich ähnlich wie die Impulswellen in fünf Wellen. Es existieren hierbei zwei Arten von Diagonalen: Beendende Diagonale und Führende Diagonale.

Beendende Diagonalen sind meist in Welle 5 und selten in Welle C zu finden. Alle Wellen, auch Welle 3 und 5, sind Korrekturwellen, hieraus ergibt sich ein 3-3-3-3-3-Muster. Die Diagonalen bewegen sich hierbei fast ausnahmslos aufeinander zu:

Führende Diagonalen treten in Welle 1 oder Welle A (sofern es ein ZigZag ist, siehe unten) auf. Hierbei überschneiden sich immer Welle 1 und Welle 4, und die Diagonalen bewegen sich aufeinander zu. Im Gegensatz zur beendenden Diagonale sind die Wellen 1, 3 und 5 Motive-Wellen, und es ergibt sich ein 5-3-5-3-5-Muster:

Korrektur-Wellen

Die Korrektur-Wellen bewegen sich entgegengesetzt des höheren Trends. Es existieren hierbei vier Hauptkategorien: Zigzag, Flat, Dreiecke und Kombinationen.

Zigzag

Der Zigzag ist eine Korrekturwelle, die drei Wellen werden mit A, B und C gekennzeichnet. Die Welle A und die Welle C stellen hierbei ihrerseits eine Motive-Welle dar und die Welle B eine Korrekturwelle, so dass sich eine 5-3-5-Sequenz gegen den übergeordneten Trend ergibt. Ein Zigzag bewegt sich mit starker Energie gegen den Trend, da dieser seinerseits zwei Motive-Wellen enthält.

Die Welle C schließt nahezu immer Unter der Welle A, und die Welle B darf den Beginn von Welle A nicht überschreiten.

In einem Zigzag läuft die Welle B niemals um mehr als 61,8 % der Welle A zurück.

Ein Zigzag stellt sich im Chart folgendermaßen dar:

Manchmal kommt es vor, dass ein Zigzag zweimal hintereinander auftritt. Ganz selten geschieht dies dreimal hintereinander. Man spricht in diesem Fall von einem Doppel-Zigzag. In diesem Fall werden die beiden Zigzags mit W, X und Y bezeichnet. Es entsteht hierdurch eine 5-3-5-3-5-3-5-Sequenz. Diese stellt sich in einem Chart folgendermaßen dar:

Flat

Neben dem Zigzag tritt häufig auch ein Flat-Muster auf. Welle A und B sind in diesem Fall Korrekturwellen, in einer 3-3-5-Sequenz. Hierdurch stellt sich der Flat schwächer gegen den Trend als der ZigZag. Im Gegensatz zum Zigzag muss die Welle C nicht unterhalb von Welle A schließen; sollte dies trotzdem erfolgen, wird von einem erweiterten Flat gesprochen.

Die Welle C darf oberhalb enden, dies ist ein verkürzter Flat. Ein Flat stellt sich daher in einer der folgenden drei Formationen dar:

Diese drei Typen der Flats sind Varianten des normalen Flat.

Sonderformen des Flats sind solche mit über- oder unterschießender Welle B. Hierbei übersteigt/überschießt Welle B Welle A (Flat in einem Aufwärtstrend) oder fällt tiefer als/unterschießt Welle A (Flat in einem Abwärtstrend).

Nach einer solchen Welle B kann die nachfolgende Welle C entweder sehr lang oder sehr kurz werden. Bei einer sehr langen Welle C (länger als 161,8 % der Welle A) spricht man von einem „irregular Flat“, bei einer sehr kurzen Welle C (mind. 61,8 % der Welle B) von einem „running Flat“.

Entscheidend bei einem Flat sind die Retracements der drei Wellen (A-B-C):

Normales Flat (auch verkürztes und erweitertes Flat):

- Welle B retraced mindestens 61,8 % von Welle A (im Unterschied zum Zigzag, bei dem die Welle B zwingend unterhalb des 61,8 % Retracements verbleiben muss).

- Welle C wird nie länger als 161,8 % der Welle A.

- Welle C erreicht mindestens 61,8 % der Welle B, meistens jedoch 61,8 % der Welle A.

„irregular Flat“:

- Welle B über- oder unterschießt Welle A (je nach Trendrichtung) maximal um 61,8 %.

- Welle C kann maximal 261,8 % der Welle A erreichen.

Der Kursverlauf „bestraft“ hiermit sozusagen die Teilnehmer, die in der Welle B über das Ziel hinausgeschossen sind.

„running Flat“:

- Welle B über- oder unterschießt Welle A (je nach Trendrichtung) maximal um 61,8 %.

- Welle C kann nur mindestens 61,8 % der Welle B erreichen.

Der Kursverlauf „belohnt“ hiermit sozusagen die Teilnehmer, die in der Welle B schon die Trendfortsetzung sahen mit einer kurzen und schnellen Welle C.

Zu den Besonderheiten gehört auch, dass die Welle C auch ein EDT (ending diagonal triangle) sein kann.

Theoretisch gibt es ähnlich dem Doppel-Zigzag die Möglichkeit von Doppel-Flats, diese werden von Elliott als normale Kombinaten in „Doppel-Drei“ und „Dreifach-Drei“ (siehe unten) behandelt und deuten auf eine ausgedehnte Seitwärtsbewegung hin.

Horizontale Dreiecke

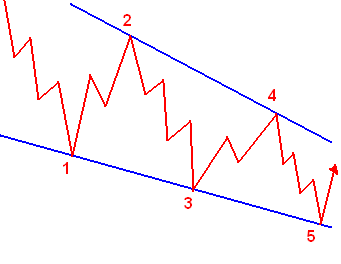
Eine Dreiecksformation bewegt sich in einer 3-3-3-3-3-Formation mit den Bezeichnungen A, B, C, D und E. Diese Formation deutet auf einen Ausgleich der Kräfte hin und die Kurse bewegen sich Seitwärts bei geringer werdenden Volumen. Die Welle E beachtet häufig nicht die Begrenzungslinie und muss daher nicht bis zu ihr laufen, kann sie aber auch überschreiten.

Es existieren zwei Varianten von Dreiecken: Zusammenlaufende und sich ausdehnende Dreiecke.

Sich ausdehnende Dreiecke kommen sehr selten vor. Bei den zusammenlaufenden Dreiecken existieren drei Varianten: symmetrische Dreiecke, aufsteigende Dreiecke und abfallende Dreiecke.

Hier eine Darstellung der Dreiecksformationen:

Kombinationen

Elliott bezeichnet die meist seitwärts laufenden Kombinationen aus zwei oder drei Korrekturwellen als „Doppel-Drei“ oder „Dreifach-Drei“. Hierbei werden die Wellen mit den Bezeichnungen W, X, Y und gegebenenfalls Z verbunden. Die Bezeichnung Z tritt hierbei nur bei „Dreifach-Drei“ auf. Die einzelnen Korrekturwellen werden mit einer 3er-Formation verbunden.

Hier einige Beispiele:

Folgende Formationen sind möglich:

• Flat-Flat
• Flat-Dreieck
• Zigzag-Flat
• ZigZag-Dreieck
• Flat-Flat-Flat
• Flat-Flat-Dreieck
• ZigZag-Flat-Flat
• Zigzag-Flat-Dreieck

Fibonacci-Zahlen

Die Wellentheorie von Elliott behauptet, dass die Aktienpreise durch Zyklen gelenkt werden, die auf der Reihenfolge der Fibonacci-Zahlen beruhen: 0, 1, 1, 2, 3, 5, 8, 13, 21, ….

Demnach bewegen sich die Märkte in einer vorherbestimmten Anzahl von Höhen und Tiefen, den Wellen. Die Marktpreise bewegen sich in fünf Wellen nach oben und in drei Wellen wieder nach unten (5-3-Sequenz). Bei einer Hausse gilt diese einfache Beobachtung als gesichert. Die erste, dritte und fünfte Welle werden Impulswellen genannt. Bei einer Baisse verhält sich der Markt umgekehrt, dann gehen fünf Wellen nach unten und drei Korrekturen nach oben.

Rezeption

In der wirtschaftswissenschaftlichen Literatur ist diese Wellentheorie gleichwohl sehr umstritten, da offensichtlich ein linearer Mechanismus der Preisentwicklung nicht mit dieser Eindeutigkeit zu belegen ist. Unbestritten ist dagegen der psychologische Faktor des Käuferverhaltens.

Eine wissenschaftliche Wiederbelebung erfuhr die Elliott-Wellen-Theorie durch die Entdeckung des mathematischen Phänomens der Fraktale Ende der 1970er Jahre. Auch hier stellt sich die Frage, ob erneut ein verkürzender Analogieschluss von mathematischen Regelmäßigkeiten auf soziale Phänomene vorliegt.

Vor allem die zutreffende Prognose des Aktienhändlers Robert Prechter von 1978 für eine allgemeine Aktienhausse bis zur Mitte der 1980er und der anschließende Crash von 1987 konnte zumindest bei einem Teil der Börsianer und Wirtschaftsjournalisten das Ansehen dieser Theorie mehren.

Unter dem Blickwinkel der Chaostheorie lassen sich die 5-3-Sequenzen, die sich – wie bei Fraktalen üblich (vgl. Mandelbrot-Fraktal) – im Sinne der Selbstähnlichkeit in unterschiedlichen Größenordnungen (entspricht Zeitabschnitten: Minuten, Stunden, Tage, Wochen, Monate, Jahre usw.) wiederholen, als Marktfraktal interpretieren.

Neuere Forschungen ergaben Hinweise darauf, dass Marktfraktale von Aktienindizes als Messinstrumente für die gesellschaftliche und historische Entwicklung eines Landes dienen können. Historische Entwicklungen und Ereignisse repräsentieren demnach endogene, durch äußere Ereignisse nicht zu beeinflussende Stimmungsschwankungen von Gesellschaften im massenpsychologischen Sinne. In gewissen Grenzen soll es möglich sein, bei korrekter Auswertung der Elliott-Wellen Voraussagen über die weitere geschichtliche, gesellschaftliche und soziale Entwicklung eines Landes zu ermöglichen. Dieser Teilbereich der Geschichts- oder Gesellschaftswissenschaft wird Socionomics genannt.

Literatur

• Prechter, Robert und Frost, A. J. (2004): Das Elliott-Wellen-Prinzip. Schlüssel für Gewinne am Markt. München: FinanzBuch Verlag, S. 327 ISBN 3-89879-038-X
• Ströer, Walter J. (1988): Die Sprache der Märkte. Elliott-Wellen; Struktur für die Zukunft. Brechen: Verlag Sprache der Märkte, 230 S., 96 graph. Darst. ISBN 3-9801956-0-0
• Maass, Rüdiger (2011): Elliott-Wellen; Sichere Prognosen in jeder Marktlage treffen. München: FinanzBuch Verlag, 232 S., ISBN 978-3-89879-338-4
• Tiedje, André (2010): Elliot-Wellen leicht verständlich. München: FinanzBuch Verlag, 240 S., ISBN 978-3-89879-503-6