Materialermüdung

aus Wikipedia, der freien Enzyklopädie
(Weitergeleitet von Ermüdungsriss)
Zur Navigation springen Zur Suche springen
Durch Materialermüdung gebrochene Hartschale eines Skischuhs

Die Materialermüdung beschreibt einen langsam voranschreitenden Schädigungsprozess in einem Werkstoff unter Umgebungseinflüssen wie wechselnder mechanischer Belastung, wechselnder Temperatur, UV-Strahlung, ionisierender Strahlung, eventuell unter zusätzlicher Einwirkung eines korrosiven Mediums.

Beschreibung

[Bearbeiten | Quelltext bearbeiten]

Materialermüdung bedeutet, dass auch eine statisch unkritische Belastung (noch im elastischen Bereich, also noch unterhalb der Streckgrenze des Werkstoffs) zu einer Funktionsuntüchtigkeit (Ermüdungsrissbildung) oder auch zum Totalausfall (Ermüdungsbruch) eines Bauteils führen kann, wenn sie oft genug auf das Bauteil einwirkt.

Zyklisch belastete Teile haben daher prinzipiell eine begrenzte Lebensdauer. Deshalb muss man an kritischen Bauteilen vor dem Einsatz eine Lebensdauerbewertung, -berechnung oder Versuche durchführen, die eine Abschätzung der Haltbarkeit des Bauteils zulassen. Bauteile, die theoretisch unbegrenzt viele Zyklen ertragen (weil sie aus bestimmten, dafür geeigneten Werkstoffen bestehen), bezeichnet man als dauerfest.

Einfaches Beispiel: Die Halterung eines Kugelschreibers kann mehrmals elastisch hin- und hergebogen werden. Mit der Anzahl der Biegevorgänge nimmt allerdings die Wahrscheinlichkeit eines Bruches zu. Die Redewendung „Steter Tropfen höhlt den Stein“ oder das philosophische Gesetz vom „Umschlagen quantitativer Veränderungen in qualitative“ beschreibt dieses Phänomen.

Die genaue Betrachtung des Bruchbildes eines Bauteils zeigt, ob ein Gewalt- oder ein Ermüdungsbruch vorliegt. Daraus müssen Schlussfolgerungen gezogen werden, um das Bauteilversagen in Zukunft zu vermeiden.[1][2]

Unterarten

[Bearbeiten | Quelltext bearbeiten]

Man unterscheidet

Isotherme mechanische Ermüdung

[Bearbeiten | Quelltext bearbeiten]

Als mechanische Materialermüdung metallischer Werkstoffe wird der Prozess bezeichnet, der letztlich zum Versagen eines Bauteils oder Werkstoffes durch Bildung eines Anrisses, Erreichen einer bestimmten Risslänge oder Ermüdungsbruch führt. Der Prozess beginnt mit lokalen Versetzungsbewegungen, die bereits bei Beanspruchungen unterhalb der Streckgrenze vor allem an der Bauteiloberfläche an Querschnittsübergängen und Oberflächenkerben oder im Volumen an Werkstoffinhomogenitäten wie Einschlüssen, Poren, Ausscheidungen, Dispersionen etc. durch lokale Spannungsüberhöhungen auftreten.

Durch wiederholte Beanspruchung bilden sich statistisch regellos verteilte Bereiche lokaler plastischer Verformungen. Im weiteren Verlauf der Beanspruchung bilden sich daraus Versetzungskonfigurationen, die schädigende Wirkung durch Konzentration plastischer Verformungen auf sehr kleine Bereiche haben können.

Das weitere Verhalten unter zyklischer Beanspruchung ist stark vom Werkstoff und seiner Vorgeschichte abhängig. Meist bilden sich in oberflächennahen Werkstoffbereichen Ermüdungsgleitbänder, sog. persistente Gleitbänder, aus, die dann unter 45° zur Beanspruchungsrichtung (höchste Schubspannung und daher bevorzugte Richtung der Versetzungsbewegung, Mohrscher Spannungskreis) sogenannte Ex- und Intrusionen an der Bauteiloberfläche bilden. Diese wirken wie scharfe Kerben und initiieren Mikrorisse, die parallel zu den Gleitbändern verlaufen. Nach einigen Mikrometern (häufig etwa doppelter Korndurchmesser des Gefüges) schwenken die Risse um und verlaufen unter 90° zur Beanspruchungsrichtung.

Bei Erreichen einer bestimmten Risslänge spricht man dann von Makrorissen oder sogenannten technischen Anrissen, die sich in Abhängigkeit von der Rissgeometrie, der Beanspruchungsart (Rissmoden) und der -höhe ausbreiten. Erreicht der Anriss die sogenannte kritische Risslänge, versagt das Bauteil durch instabile Rissausbreitung (Gewaltbruch) im Restquerschnitt.

Geschichtliche Ereignisse

[Bearbeiten | Quelltext bearbeiten]
In Concepción stürzte der 21-stöckige O’Higgins Tower teilweise ein. Das Erdbeben von 2010 in Chile verursachte Ermüdungsbrüche in Strukturelementen.[3]
  • 1822: Thomas Tredgold veröffentlicht A Practical Essay on the Strength of Cast Iron and other Metals
  • 1829: Julius Albert beobachtet Ausfälle an eisernen Kettengliedern von Minen-Fahrstühlen in den Minen von Clausthal
  • 1839: In seinen Vorlesungen an der Militärschule in Metz führt Jean Victor Poncelet den Begriff der Ermüdung an Metallen ein und vergleicht es mit dem Erschlaffen eines Menschen
  • 1843: William John Macquorn Rankine erkennt die Wichtigkeit der Spannungskonzentration in seinen Untersuchungen an Ausfällen von Eisenbahn-Achsen im Zugunglück von Versailles
  • 1849: Eaton Hodgkinson untersucht, bis zu welcher Grenze man Stahlstrukturen belasten kann ohne die Sicherheit zu gefährden
  • 1860: August Wöhler untersucht Eisenbahnachsen und schlägt daraufhin vor, die Belastungsgrenzen von Bauteilen in einem Diagramm aufzutragen, um zukünftig Festigkeits-Auslegungen zu ermöglichen[4]
  • 1875: Die Lokomotive Amstetten entgleist aufgrund eines wegen Materialermüdung gebrochenen Radreifens. Die Untersuchung des Unfalls gilt als der Beginn der modernen Materialprüfung und -normung
  • 1903: Sir James Alfred Ewing entdeckt mikroskopisch kleine Risse als den Ursprung des Ermüdungsversagens
  • 1910: O.H. Basquin definiert die Form einer typischen Wöhlerkurve
  • 1938: Edward E. Simmons erfindet den Dehnungsmessstreifen und beschleunigt damit sämtliche Forschung auf dem Gebiet der Ermüdung
  • 1945: A.M. Miner favorisiert A. Palmgrens (1924) lineare Schadensakkumulations-Theorie als praktikables Auslegungswerkzeug
  • 1954: Materialermüdung führt zu einer zunächst rätselhaften Serie von Abstürzen von De Havilland DH.106 Comet-Jets, den ersten kommerziellen Passagierjets.
  • 1954: L.F. Coffin und S.S. Manson erklären das Risswachstum anhand plastischer Dehnungen an der Rissspitze
  • 1961: P.C. Paris stellt den phänomenologischen Betrachtungen Miners seine theoretische Betrachtungen auf Basis des Risswachstums einzelner Risse gegenüber
  • 1968: Tatsuo Endo und M. Matsuiski leiten den Rainflow-Algorithmus zur Zählung von zufälligen Schwingspielen ab und ermöglichen damit die zuverlässige Anwendung der Minerschen Gesetzmäßigkeiten
  • 1970: W. Elber entdeckt die Mechanismen des Riss-Schließens
  • 1975: S. Pearson beobachtet bei kurzen Rissen gelegentliches Stoppen des Risswachstums in frühen Wachstumsphasen
  • 1975: J. Köhler bestätigt den statistischen Größeneinfluss aus der Extremwerttheorie nach W. Weibull und E. J. Gumbel
  • 1980: Durch Ermüdungserscheinungen am Tragwerk der Bohrinsel Alexander L. Kielland sterben 123 der 212 Besatzungsmitglieder. Dies führte u. a. zu einer Reihe von einschneidenden Änderungen in der Konstruktion und Prüfung von Bohrinseln
  • 1998: Ein wegen Materialermüdung gebrochener Radreifen führt zum ICE-Unfall von Eschede, dem weltweit schwersten Unglück eines Hochgeschwindigkeitszuges
  • 2010: Ein weiteres Ereignis aus jüngerer Zeit war das Erdbeben in Chile im Jahr 2010, bei dem mehrere Forscher der Universität von Chile Berichte über mehrere im ganzen Land durch das seismische Ereignis beschädigte Stahlbetonkonstruktionen berichteten. Viele Strukturelemente wie Balken, Wände und Stützen versagten aufgrund von Ermüdung, wodurch die bei der Konstruktion verwendeten Stahlbewehrungen mit deutlichen Anzeichen von Längsknicken.[5][6] Dieses Ereignis führte dazu, dass die chilenischen seismischen Bemessungsnormen auf der Grundlage von Beobachtungen an beschädigten Strukturen, die durch das Erdbeben verursacht wurden, aktualisiert wurden.[7]

Schwingende Beanspruchung

[Bearbeiten | Quelltext bearbeiten]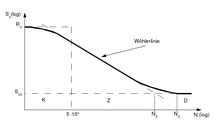
Qualitative Darstellung der Wöhlerlinie
Das Haigh-Diagramm ist ein Schaubild zur Bestimmung von Dauerfestigkeit

Materialermüdung kann durch schwingende, dynamische Belastung auftreten. Die Spannung, bei der ein dynamisch belastetes Bauteil bricht, liegt jedoch deutlich unterhalb der Zugfestigkeit und meist auch unterhalb der Streckgrenze des verwendeten Werkstoffs. Die Schwingfestigkeit von Werkstoffen oder Bauteilen wird im Wöhlerversuch ermittelt. Hierfür werden die Versuchskörper zyklisch, meist unter einer sinusförmigen Beanspruchungs-Zeit-Funktion, belastet. Der Versuch läuft, bis ein definiertes Versagen (Bruch, Anriss) eintritt oder eine festgelegte Grenzschwingspielzahl erreicht wird. Versuchskörper, die die Grenzschwingspielzahl ohne erkennbares Versagen erreichen, werden als Durchläufer bezeichnet.

Die Ergebnisse des Versuchs trägt man in ein doppellogarithmisches Diagramm ein. Üblicherweise wird im Wöhlerdiagramm die Nennspannungsamplitude Sa über der ertragbaren Schwingspielzahl aufgetragen. Den sich ergebenden Kurvenzug nennt man die Wöhlerkurve oder auch Wöhlerlinie. In der nebenstehenden Wöhlerkurve sind die drei Bereiche K, Z und D eingetragen.

  • K ist der Bereich der Kurzzeitfestigkeit bzw. Kurzzeitschwingfestigkeit unterhalb von ca. 104 bis 105 Schwingspielen. Diese Art der Ermüdung tritt bei hohen plastischen Dehnamplituden auf, die zu frühem Versagen führen. Um diesen Bereich genauer darzustellen, wird in der Regel die Coffin-Manson-Auftragung herangezogen.
  • Z ist der Bereich der Zeitfestigkeit bzw. Zeitschwingfestigkeit zwischen 104 und materialabhängig etwa 2·106 Schwingspielen, in dem die Wöhlerkurve bei doppellogarithmischer Darstellung nahezu gerade verläuft.
  • D ist der anschließende Bereich der so genannten Dauerfestigkeit. Bei ferritisch-perlitischen Stählen beginnt der Bereich der Dauerfestigkeit bei ca. 1–5·106. Bei austenitischen Stählen und kfz Basiswerkstoffen (z. B. Aluminium, Gold, Kupfer) fällt die ertragbare Amplitude weiter ab. Eine „echte“ Dauerfestigkeit existiert hier nicht. Daher wird hier meist die ertragbare Amplitude bei 107 Lastwechseln als Dauerfestigkeit bezeichnet. Unterliegt ein Bauteil ständiger Korrosion oder stark erhöhten Temperaturen, so kann nicht mehr mit einer Dauerfestigkeit gerechnet werden. Zur Bestimmung der Dauerfestigkeit werden Schaubilder wie das Haigh-Diagramm oder das Smith-Diagramm verwendet.[8]

Unterhalb der Dauerfestigkeit SaD kann ein Bauteil prinzipiell beliebig viele Schwingspiele ertragen. Belastungen oberhalb der Dauerfestigkeit bewirken ein Versagen des Bauteils nach einer bestimmten Zahl an Schwingspielen. Die Zahl der ertragenen Schwingspiele eines Bauteils unter Betriebsbelastung (variable Belastungsamplituden) bis zum Ausfall kann im Rahmen statistischer Genauigkeit mit Hilfe der Wöhlerlinie vorausgesagt werden. Dazu verwendet man die Methoden der linearen Schadensakkumulation nach Palmgren, Langer und Miner. Man spricht hierbei von betriebsfester Bemessung eines Bauteils. Betriebsfestigkeit wird heute in nahezu allen Bereichen der Technik zum Zweck des Leichtbaus eingesetzt.

Siehe auch

[Bearbeiten | Quelltext bearbeiten]

Literatur

[Bearbeiten | Quelltext bearbeiten]
  • S. Suresh: Fatigue of Materials. Cambridge University Press, 1998.
  • Bernhard Ilschner: Hochtemperatur-Plastizität. Springer-Verlag, 1973.
  • Joachim Rösler, Harald Harders, Martin Bäker: Mechanisches Verhalten der Werkstoffe. Teubner, 2006.
  • Richard M. Christensen: The theory of materials failure. Oxford Univ. Press, Oxford 2013, ISBN 978-0-19-966211-1.
[Bearbeiten | Quelltext bearbeiten]
Wiktionary: Materialermüdung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

[Bearbeiten | Quelltext bearbeiten]
  1. ↑ W. Olivier, R. Jaeger, M. Möser, K. Müller: Schadensanalyse eines Misserfolgs durch Implantatfraktur. In: Implantologie Journal, 7(6), 2003, Oemus Media Leipzig, S. 34–36, ISSN 1435-6139
  2. ↑ K. Müller, W. Olivier, R. Jaeger, M. Möser: Schadensanalysen an enossalen Titanimplantaten. (Memento vom 28. April 2015 im Internet Archive) (PDF) Postersession, DGI Tagung Göttingen 27.–29. November 2003
  3. ↑ F. Rojas et al.: Performance of tall buildings in Concepción during the 27 February 2010 moment magnitude 8.8 offshore Maule, Chile earthquake. In: The Structural Design of Tall and Special buildings. 20. Jahrgang, Nr. 1, 2011, S. 37–64, doi:10.1002/tal.674 (wiley.com).
  4. ↑ K.-E. Kurrer: Wenn Eisenbahnräder müde werden In: der Freitag Nr. 15/2004, 2. April 2004, S. 18.
  5. ↑ J. E. Egger, F. R. Rojas, L. M. Massone: High-Strength Reinforcing Steel Bars: Low Cycle Fatigue Behavior Using RGB Methodology. In: International Journal of Concrete Structures and Materials. 15. Jahrgang, Nr. 38, 24. September 2021, doi:10.1186/s40069-021-00474-9 (springer.com).
  6. ↑ L. M. Massone, P.A. Herrera: Experimental study of the residual fatigue life of reinforcement bars damaged by an earthquake. In: Materials and Structures. 52. Jahrgang, Nr. 61, 22. Mai 2019, doi:10.1617/s11527-019-1361-x (springer.com).
  7. ↑ J. Wallace, L. Massone, P. Bonelli, J. Dragovich, R. Lagos, C. Lüders, J. Moehle: Damage and implications for seismic design of RC structural wall buildings. In: Earthquake Spectra. 28. Jahrgang, Nr. 2, 2012, S. 281–299, doi:10.1193/1.4000047.
  8. ↑ Georg Jacobs: Maschinengestaltung. Mainz Verlag, Aachen 2015, ISBN 3-86130-748-0, S. 19–21.
Abgerufen von „https://de.wikipedia.org/w/index.php?title=Materialermüdung&oldid=246989878“