Newtonsche Gesetze

Im Jahr 1687 erschien Isaac Newtons Werk Philosophiae Naturalis Principia Mathematica (lat.; ‚Mathematische Prinzipien der Naturphilosophie‘), in dem Newton drei Grundsätze der Bewegungslehre formuliert, die als die Newtonschen Axiome, Grundgesetze der Bewegung, Newtonsche Prinzipien oder auch Newtonsche Gesetze bekannt sind. Sie werden in Newtons Werk mit Lex prima, Lex secunda und Lex tertia (‚Erstes/Zweites/Drittes Gesetz‘) bezeichnet, oder zusammengenommen mit axiomata, sive leges motus (‚Axiome oder Gesetze der Bewegung‘).
Diese Gesetze bilden das Fundament der Klassischen Mechanik. Obwohl sie im Rahmen moderner physikalischer Theorien wie der Quantenmechanik und der Relativitätstheorie nicht uneingeschränkt gelten, sind mit ihrer Hilfe innerhalb des weiten Gültigkeitsbereiches der klassischen Mechanik zuverlässige Vorhersagen möglich.
Meistens werden die drei Gesetze in vereinfachter Form so wiedergegeben:
- Ein kräftefreier Körper bleibt in Ruhe oder bewegt sich geradlinig mit konstanter Geschwindigkeit.
- Kraft gleich Masse mal Beschleunigung:
- Kraft gleich Gegenkraft: Eine Kraft von Körper A auf Körper B geht immer mit einer gleich großen, aber entgegen gerichteten Kraft von Körper B auf Körper A einher:
Zudem ging Newton davon aus, dass zwei Kräfte mit einem Kräfteparallelogramm zu einer resultierenden Kraft zusammengefasst werden können. Das Axiom vom Kräfteparallelogramm wurde auch als viertes Newtonsches Gesetz bezeichnet, während in moderner Literatur meist das allgemeinere Superpositionsprinzip als viertes Newtonsches Gesetz genannt wird.
Überblick
Erstes Newtonsches Gesetz
Das erste Newtonsche Gesetz wird auch lex prima, Trägheitsprinzip, Trägheitsgesetz oder Inertialgesetz genannt. Das Trägheitsprinzip macht Aussagen über die Bewegung von physikalischen Körpern in Inertialsystemen:
- „Ein Körper verharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, sofern jener nicht durch einwirkende Kräfte zur Änderung seines Zustands gezwungen wird.“
Lateinischer Originaltext:
- Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.[1]
Die Geschwindigkeit ist also in Betrag und Richtung konstant. Eine Änderung des Bewegungszustandes kann nur durch Ausübung einer Kraft von außen erreicht werden, beispielsweise durch die Gravitationskraft oder die Reibungskraft. Man beachte, dass innere Kräfte, also Kräfte zwischen den Teilen eines zusammengesetzten Körpers, seine Bewegung als Ganzes nicht beeinflussen.
Andere Formulierungen lauten:
- Wirkt auf einen Körper keine Kraft, so ist seine Geschwindigkeit zeitlich konstant.[2]
- Wenn auf einen Massenpunkt keine Kraft wirkt, so ist sein Impuls konstant.[3] Dabei ist der Impuls das Produkt aus Masse und Geschwindigkeit.
Daraus folgt nicht, dass gar keine Kraft wirkt, wenn er sich mit konstanter Geschwindigkeit bewegt. Dasselbe Ergebnis tritt nämlich auch dann ein, wenn mehrere Kräfte auf ihn wirken, die einander in ihrer Wirkung aufheben. In diesem Fall befindet er sich im Kräftegleichgewicht und es wirkt keine resultierende Kraft.
Die obigen Fassungen gelten nur dann, wenn die Bewegung in einem Inertialsystem beschrieben wird. Das erste Newtonsche Gesetz ist dann lediglich ein Spezialfall des zweiten.[4] In den modernen Werken zur theoretischen Mechanik wird meist zunächst das Bezugssystem definiert und das erste Newtonsche Gesetz in der folgenden oder einer ähnlichen Fassung eingeführt.
- Es gibt Koordinatensysteme, in denen sich jeder kräftefreie Massepunkt geradlinig gleichförmig bewegt oder ruht. Diese besonders wichtigen Koordinatensysteme werden Inertialsysteme genannt.[5]
Das erste Newtonsche Axiom wird somit als Definition für den Begriff des Inertialsystems genutzt.
Zweites Newtonsches Gesetz

Das zweite Newtonsche Gesetz wird auch lex secunda, Aktionsprinzip oder (in der Technischen Mechanik) Impulssatz genannt,[6] wobei jedoch mit letzterem in der Physik nur der Impulserhaltungssatz bezeichnet wird.
Es ist die Grundlage für viele Bewegungsgleichungen der Mechanik:
- „Die Änderung der Bewegung ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.“
Lateinischer Originaltext:
- „Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.“
Formal wird dieser Zusammenhang zwischen Kraft und Bewegungsänderung als ausgedrückt, beziehungsweise als . Hierbei sind die Änderungsrate der Geschwindigkeit, also die Beschleunigung, und die Änderungsrate des Impulses. bezeichnet die resultierende äußere Kraft. Sofern für die Kraft eine kohärente Einheit verwendet wird, wie beispielsweise Newton im internationalen Einheitensystem, so kann die letzte Beziehung auch als Gleichung geschrieben werden:
Ersetzt man in dieser Gleichung den Impuls durch , so erhält man , beziehungsweise
mit der Beschleunigung . Vor allem in der letzten Schreibweise wird diese Beziehung häufig als Grundgleichung der Mechanik bezeichnet. Sie wurde in dieser Weise erstmals 1750 von Leonhard Euler formuliert.[7] Für die Bewegung in einer Dimension, d. h. ohne Änderung der Richtung, geht die Formulierung auf Jakob Hermann zurück.
In seinem Originalwerk hat Newton für die einwirkende Kraft und die resultierende Bewegungsänderung eine Proportionalität postuliert. Er arbeitete, wie in seiner Zeit üblich, vorrangig mit Quotienten zweier gleichartiger Dinge, nicht mit Quotienten (oder Produkten) von Dingen verschiedener Art. Die mathematische Gleichsetzung von begrifflich so verschiedenen Dingen wie Kraft und Impulsänderung (genauer: Impulsänderungsrate) wurde erst später von Leonhard Euler (in der Form ) und d’Alembert (in der Form für die der Veränderung des Bewegungszustandes entgegengesetzte Trägheitskraft) formuliert.[8]
Die Darstellung wird auch als Impulssatz bezeichnet, vor allem in Literatur zur Technischen Mechanik und zur Strömungslehre. In Worten ausgedrückt bedeutet sie, dass die zeitliche Änderung des Impulses eines Körpers der resultierenden äußeren Kraft entspricht, die auf diesen Körper wirkt. Diese Darstellung ist allgemeiner als die darunter genannte Form von Euler, da sie auch Bewegungen von Körpern mit veränderlicher Masse (beispielsweise Raketen) beschreibt. Das 2. Newtonsche Gesetz kann auch in integraler Form dargestellt werden:
Das Integral der Kraft über die Zeit oder (im Falle einer konstanten Kraft) das Produkt aus Kraft und Einwirkungsdauer wird auch als Kraftstoß bezeichnet. Die Kraft kann somit als Ursache für die Änderung des Impulses gedeutet werden. Kräfte, die parallel oder antiparallel zur Bewegungsrichtung wirken, verändern den Betrag des Impulses; wirken sie rechtwinklig zur Bewegung, so ändern sie dessen Richtung; Kräfte, die schiefwinklig angreifen, beeinflussen beides. Falls die resultierende Kraft null ist, folgt daraus der Impulserhaltungssatz.[9][10][11][12] (siehe Erstes Newtonsches Gesetz)
Drittes Newtonsches Gesetz
Das dritte Newtonsche Gesetz, auch lex tertia, Wechselwirkungsprinzip, Gegenwirkungsprinzip, oder Reaktionsprinzip genannt, besagt:
- „Kräfte treten immer paarweise auf. Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio), so wirkt eine gleich große, aber entgegen gerichtete Kraft von Körper B auf Körper A (reactio).“
Lateinischer Originaltext:
- „Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.“
Das Wechselwirkungsprinzip wird auch als Prinzip von actio und reactio bezeichnet.
Im Unterschied zum Kräftegleichgewicht wirken die beiden Kräfte und nicht auf denselben, sondern auf verschiedene Körper. Sie heben sich also nicht gegenseitig auf.
Das dritte Newtonsche Gesetz setzt voraus, dass die Wirkung der wechselseitigen Kräfte auf beide Körper unmittelbar, also gleichzeitig erfolgt. Während das bei Körpern, die sich direkt berühren, naheliegend ist, macht es bei weit voneinander entfernten Körpern eine unverzügliche Fernwirkung erforderlich. Dies ist nach heutigem Verständnis der Physik nicht möglich. In der speziellen Relativitätstheorie (und damit der Elektrodynamik) und der allgemeinen Relativitätstheorie zeigt sich, dass das dritte Newtonsche Gesetz nicht immer anwendbar ist – verwendbar ist weiterhin die Impulserhaltung des Gesamtsystems (Teilchen plus Feld).[13] Der Unterschied zwischen der von Newton postulierten Fernwirkung und der verzögerten Kraftübertragung durch Felder wirkt sich vor allem auf relativ zueinander bewegte Körper aus, die Verzögerung ist gut durch Beobachtungen bestätigt.
Das Wechselwirkungsprinzip lässt sich auch so formulieren, dass in einem aus mehreren Körpern bestehenden System die Vektorsumme der Kräfte zwischen den Körpern gleich Null ist.
Superpositionsprinzip der Kräfte
In Newtons Werk wird das Prinzip der ungestörten Überlagerung oder Superpositionsprinzip der Mechanik als Zusatz zu den Bewegungsgesetzen beschrieben.
- „Wirken auf einen Punkt (oder einen starren Körper) mehrere Kräfte , so addieren sich diese vektoriell zu einer resultierenden Kraft auf.“
Später wurde dieses Superpositionsprinzip auch als lex quarta, als viertes Newtonsches Gesetz bezeichnet.
Anwendung
Last an einer festen Rolle
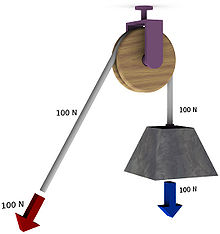
Als einfaches Anwendungsbeispiel soll hier eine Last dienen, die an einem Seil hängt, das über eine feste Rolle läuft (siehe Abbildung).
- Auf die Last wirkt eine Gewichtskraft von (beispielsweise) 100 N nach unten. Gleichzeitig wirkt durch das gespannte Seil auf die Last eine Kraft von 100 N nach oben. Diese beide Kräfte heben sich auf. Die Last befindet sich also im Kräftegleichgewicht. Nach dem ersten Newtonschen Gesetz befindet sie sich entweder in Ruhe oder bewegt sich mit konstanter Geschwindigkeit auf oder ab. Entgegen der Intuition ist für das Heben und Senken einer Last die gleiche Kraft erforderlich.
- Wenn man das Seil loslässt, wird die Last immer noch mit einer Kraft von 100 N nach unten gezogen. Es fehlt aber die nach oben gerichtete Kraft. Nach dem zweiten Newtonschen Gesetz beginnt die Last nun beschleunigt nach unten zu fallen. Die Fallbeschleunigung berechnet sich nach der Grundgleichung der Mechanik aus der Kraft und der Masse der Last: . Offensichtlich hängt diese Beschleunigung nur vom Schwerefeld der Erde, nicht aber von der Masse der Last ab. (Mit anderen Worten: Auf der Erde fallen alle Körper gleich schnell, sofern andere Kräfte als die Gewichtskraft zu vernachlässigen sind).
- Wenn ein Mensch mit der Kraft nach unten zieht, die in der Abbildung durch den roten Pfeil dargestellt wird, so erfährt er selbst nach dem dritten Newtonschen Gesetz eine nach oben wirkende Kraft. Dies wird spätestens dann offensichtlich, wenn er versucht, eine Last anzuheben, die schwerer ist als er selbst.
- Auch die Gewichtskraft, die den frei fallenden Körper nach unten beschleunigt (actio), bewirkt eine entgegengesetzte, also nach oben gerichtete Kraft (reactio). Da die Gewichtskraft von der Gravitation der Erde hervorgerufen wird, muss also diese ebenso große Kraft auf die Erde wirken. Wegen ihrer enormen Masse ist die Beschleunigung der Erde nach oben aber nicht zu bemerken.
- Man könnte den zweiten Punkt auch anders betrachten: Sobald man das Seil loslässt, wirkt keine (offensichtliche) Kraft mehr auf die Last. Betrachtet man den nun eintretenden Zustand als kräftefrei, so folgt nach dem ersten Newtonschen Gesetz, dass das Bezugssystem, in dem die frei fallende Last ruht, ein Inertialsystem ist. Demnach ist die zuvor wirksame Seilkraft nach dem zweiten Newtonschen Gesetz als eine nach oben beschleunigende Kraft zu sehen. Das Gewicht der Last ist dann nichts anderes als die Trägheit, die sich einer Beschleunigung nach oben widersetzt. Die Überlegung, dass diese Betrachtungsweise ebenso korrekt ist wie die weiter oben beschriebene, führt zum Äquivalenzprinzip der allgemeinen Relativitätstheorie.
Horizontales Federpendel (Harmonischer Oszillator)

Eine Masse kann sich reibungsfrei in horizontaler Richtung bewegen. Sie ist über eine Feder mit der Wand verbunden. Am Ort ist die Feder entspannt. Die Masse erfährt in horizontaler Richtung keine Kraft. Man bezeichnet diese Position auch als „Gleichgewichtslage“, da hier Kräftegleichgewicht herrscht. (In vertikaler Richtung wirkt die Gewichtskraft nach unten und die Stützkraft des Bodens nach oben. Diese beiden Kräfte heben sich gegenseitig auf. Da sich daran während der gesamten Bewegung der Masse nichts ändert, werden diese beiden Kräfte im Weiteren nicht mehr berücksichtigt).
- Um die Feder um die Strecke zu dehnen, ist nach dem Hookeschen Gesetz eine Kraft erforderlich. Folglich übt die Feder nach dem dritten Newtonschen Gesetz die Gegenkraft auf die Masse aus. Das negative Vorzeichen zeigt an, dass die Kraft entgegen der Auslenkung stets zur Gleichgewichtslage hin wirkt.
- Da nur in der Gleichgewichtslage keine Kraft wirkt, ist es nach dem ersten Newtonschen Gesetz nur dort möglich, dass der Körper in Ruhe verharrt. An jedem anderen Ort wird er mehr oder weniger stark beschleunigt.
- Nach dem zweiten Newtonschen Gesetz gilt
- Die Beschleunigung ist per Definition die zweite zeitliche Ableitung des Orts: . Es ergibt sich also eine lineare, homogene Differentialgleichung zweiter Ordnung:
- Die Lösungen dieser Differentialgleichungen sind zeitlich periodische Funktionen der Gestalt . Die Masse kann also Schwingungen um die Gleichgewichtslage ausführen. Die Parameter und ergeben sich aus den Anfangsbedingungen, die Kreisfrequenz aus der Masse und der Federhärte: .
Geschichte
Als Erster erkannte Galileo Galilei zu Beginn des 17. Jahrhunderts das Trägheitsprinzip und formulierte auch schon, dass die kräftefreie Bewegung sich beliebig weit geradlinig fortsetze. Er nutzte dies zur ersten korrekten Behandlung der Bewegungen von Körpern auf der Erde im freien Fall, im schiefen Wurf und auf der schiefen Ebene.[14][15] Die erste eindeutige Formulierung als allgemeines Prinzip der kräftefreien Bewegungen gab René Descartes 1644. Bereits vor der Newtonschen Formulierung als erstes Axiom (Lex Prima), ab Mitte des 17. Jahrhunderts, war das Trägheitsprinzip der Ausgangspunkt zur Begründung verschiedener mechanischer Gesetzmäßigkeiten, wie vor allem aus der Stoßtheorie und der Theorie starrer Körper. In diesem Sinne ist das Trägheitsprinzip in der zeitlich vorausgehenden Mechanik von Christiaan Huygens fest verankert.[16] Newton war dann der Erste, der das Trägheitsprinzip auch zur Begründung von Gesetzen der Himmelsmechanik einbrachte und somit auf die Bewegung der irdischen Körper und der Himmelskörper verallgemeinerte. Darin besteht auch seine besondere Leistung.[17] In den Werken der Antike, die noch bis ins Spätmittelalter als korrekt angesehen wurden, war man der Meinung, dass die Bewegungen auf der Erde und diejenigen am Himmel verschiedenen Gesetzmäßigkeiten gehorchen. Newton erkannte sie als zwei Spezialfälle eines allgemeinen Gesetzes. Außerdem erklärte Newton damit die geradlinige, unbeschleunigte Bewegung zum Normalfall. Nur wenn die Bewegung eines Körpers davon abweicht, muss man dies mit der Wirkung von Kräften erklären. Noch kurz vor Newton ging man davon aus, dass die Kreisbewegung der Normalfall wäre.[18]
Literatur
- Isaac Newton: Philosophiae Naturalis Principia Mathematica. 3. Auflage. Innys, Regiae Societatis typographos, London 1726 (uni-goettingen.de [abgerufen am 30. Juli 2017]).
- Jerry Marion, Stephen Thornton: Classical Dynamics of Particles and Systems. Harcourt College Publishers, 1995, ISBN 0-03-097302-3.
- G. R. Fowles, G. L. Cassiday: Analytical Mechanics. 6. Auflage. Saunders College Publishing, 1999, ISBN 0-03-022317-2.
- Ulrich Hoyer: Ist das zweite Newtonsche Bewegungsaxiom ein Naturgesetz? In: Zeitschrift für allgemeine Wissenschaftstheorie. Band VIII, 1977, S. 292–301, doi:10.1007/BF01800698.
Weblinks
Einzelnachweise
- ↑ Philosophiae naturalis principia mathematica. London, 1726 S. 13 (GDZ) – fast ebenso in der Auflage Genf 1739, S. 20 (Digitalisat, 60 of 589): „Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.“
- ↑ Brandt, Damen: Mechanik – Vom Massenpunkt zum starren Körper. Springer, 2016, S. 12.
- ↑ Gross et al.: Technische Mechanik – Kinetik. 13. Auflage. Springer, 2015, S. 36.
- ↑ Bartelmann et al. (Hrsg.): Theoretische Physik. Springer, 2015, S. 10.
- ↑ Tobias Henz, Gerald Langhanke: Pfade durch die Theoretische Mechanik 1. Springer, 2016, S. 42.
Beinahe gleichlautend auch bei Nolting: Grundkurs Theoretische Physik 1 – Klassische Mechanik. Die Newtonsche Mechanik und ihre mathematischen Grundlagen: anschaulich – axiomatisch – abstrakt. 10. Auflage. Springer, 2013, S. 173. - ↑ Mathias Fraaß: Impulssatz. (PDF) beuth-hochschule.de, 2006, abgerufen am 1. September 2020.
- ↑ L. Euler: Découverte d'un nouveau principe de mécanique. Memoires de l’Academie royal des sciences, Berlin, Band 6, 1752, S. 185 – Euler Opera Omnia, Serie 2, Band 5, 1957.
- ↑ H. Schecker: Der Weg zum physikalischen Kraftbegriff von Aristoteles bis Newton. In: Naturwissenschaften im Unterricht Physik/Chemie. 36, Nr. 34, 1988, (gekürzte Fassung ( vom 20. Januar 2012 im Internet Archive)).
- ↑ Dreyer: Technische Mechanik – Kinetik, Kinematik. 11. Auflage. Springer, S. 123–125.
- ↑ Holzmann, Meyer, Schumpich: Technische Mechanik – Kinetik und Kinematik. 12. Auflage. Springer, S. 123–125.
- ↑ Mahnken: Technische Mechanik – Dynamik. 2. Auflage. Springer, S. 329 f.
- ↑ Henz, Langhake: Pfade durch die Theoretische Mechanik 1. Springer, 2016, S. 140.
- ↑ Skriptum Elektrodynamik und Relativitätstheorie, S. 4 (PDF; 13,4 MB).
- ↑ Stillman Drake: Galileo and the Law of Inertia. In: American Journal of Physics. Band 32, 1964, S. 601–608, doi:10.1119/1.1970872.
- ↑ Roberto Torretti: The Philosophy of Physics. Cambridge University Press, Cambridge 1999, S. 20–30.
- ↑ David Speiser, Le ‘Horologium Oscillatorium‘ de Huygens et le ‘Principia‘. In: Revue Philosophique de Louvain, Vol. 86 (4), 1988, S. 485–504.
- ↑ Lichtenegger: Schlüsselkonzepte zur Physik – von den Newton-Axiomen bis zur Hawking-Strahlung. Springer, 2015, S. 14.
- ↑ Wilfried Kuhn: Ideengeschichte der Physik. Springer, 2. Auflage, 2016, S. 218.

































