Fast-and-Frugal-Tree

Ein Fast-and-Frugal-Tree (FFT) ist eine Darstellung von Entscheidungsregeln in Form eines Baumdiagramms. Gegenüber anderen Entscheidungsbäumen zeichnet sie sich dadurch aus, dass sie in ihrer Konstruktion und Ausführung sehr einfach gehalten ist und sich so mit wenig Eingangsinformationen schnell ausführen lassen kann.

FFTs werden in Bereichen genutzt, in denen Menschen außergewöhnlich schnelle Entscheidungen treffen müssen, so zum Beispiel in der Medizin oder dem Militär. Außerdem untersucht und verwendet man Fast-and-Frugal-Trees in der Psychologie und bei Klassifikationsverfahren im Bereich der künstlichen Intelligenz.

Mathematisch können Fast-and-Frugal-Trees als lexikographische Heuristik oder als lineares Klassifikationsverfahren mit nicht-kompensatorischen Gewichten und einem Schwellenwert verstanden werden.

Geschichte

Die Bezeichnung und das dahinter stehende Konzept wurde 2003 erstmals von Martignon, Vitouch, Takezawa und Forster vorgestellt. FFTs bauen zusammen mit anderen Heuristiken auf Modellen von Gerd Gigerenzer und Herbert A. Simon auf.

Ihre formalen Eigenschaften und ihr Aufbau wurden 2011 von Luan, Schooler und Gigerenzer mithilfe der Signalentdeckungstheorie analysiert.

Aufbau und Funktionsweise

Für Klassifikationen mit zwei möglichen Ergebnissen und n Entscheidungen lässt sich ein Fast-and-Frugal-Tree wie folgt definieren:

Ein Fast-and-Frugal-Tree ist ein Klassifizierungs- oder Entscheidungsbaum mit n+1 Blättern mit je einem Blatt für die ersten n-1 Knoten und 2 Blättern für den letzten Knoten.

Aufbau

Fast-and-Frugal-Trees stellen grundlegend eine Abfolge von Entscheidungen dar. FFTs sind so geordnet, dass sich auf jeder Ebene außer der letzten eine Entscheidung befindet. Zusätzlich befindet sich auf jeder Ebene ein Ausgang, außer auf der ersten, auf der es nur eine Entscheidung gibt und der letzten, auf welcher sich zwei Ausgänge befinden. Bei jeder Entscheidung wird eine Frage gestellt. Die Antwort einer solchen Entscheidungsfrage kann entweder zu einer weiteren Entscheidung oder einem Ausgang des FFTs führen, dieser Ausgang gibt das Ergebnis der Klassifikation an.

In der Literatur zu FFTs werden viele Algorithmen präsentiert, um Entscheidungen zu ordnen und um zu entscheiden, welche mögliche Antwort auf eine Entscheidungsfrage unmittelbar zu einem Ausgang führt. Um den Aufbau einfach und intuitiv zu halten, verwenden die Algorithmen oft einfache Maße für die Güte der Knoten (z. B. der Zusammenhang zwischen der Entscheidung und dem Ergebnis) und treffen einfache Entscheidungen über Ausgänge (über eine bestimmte Entscheidungsfrage wird unabhängig von den anderen Entscheidungen entschieden).

Abbildung 1: Ein FFT, der Ärzten bei der Entscheidung hilft, ob ein Patient auf einer normalen oder einer kardiologischen Station aufgenommen werden soll.

Ausführung

FFTs werden ab dem Wurzelknoten beginnend Knoten für Knoten abgearbeitet. Daraus ergibt sich, dass die dem Knoten zugehörige Frage beantwortet wird und in Abhängigkeit dieser Antwort das folgende Baumelement der darunterliegenden Ebene bearbeitet wird. Auf jeden Knoten folgt entweder ein Blatt, welches ein Ergebnis der Kategorisierung darstellt und damit die Ausführung des FFTs beendet, oder ein weiterer Knoten, dann wird mit dem Abarbeiten der Knoten fortgesetzt, bis ein Blatt erreicht wird.

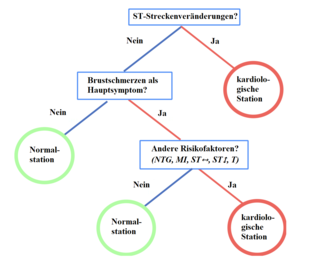
Abbildung 1 zeigt einen FFT, mit welchem entschieden werden soll, ob ein Patient in akuter Gefahr ist, einen Herzinfarkt zu erleiden. Es ergeben sich demzufolge also zwei Ausgänge: Den Patienten an die Kardiologie zu überweisen (hohes Risiko) oder ihn auf einer normalen Station aufzunehmen (geringes Risiko). Beispielhaft lässt sich der FFT an den Patienten Max, Erika und Otto anwenden.

• Bei Max wurde mittels Elektrokardiogramm eine ST-Streckenveränderung diagnostiziert. Damit wird ein „hohes Risiko“ festgestellt und er wird direkt der Kardiologie übergeben, ohne dass andere Knoten berücksichtigt wurden.
• Bei Erika lässt sich keine ST-Streckenveränderung feststellen. Zudem leidet sie unter Brustschmerzen, allerdings lassen sich keine der weiteren Risikofaktoren bei ihr feststellen. Deshalb wird sie mit geringem Risiko in einer Normalstation aufgenommen.
• Otto hat weder ST-Streckenänderungen noch Brustschmerzen, weswegen er mit „geringem Risiko“ nach zwei bearbeiteten Knoten des FFT an die Normalstation verwiesen wird.

Signalentdeckungstheorie

FFTs werden verwendet, um binäre Klassifikationen durchzuführen. Dabei wird die Signalentdeckungstheorie zur Analyse dieser Klassifizierungsaufgaben eingesetzt. Die Signalentdeckungstheorie setzt voraus, dass es zwei Kategorien von Ereignissen oder Objekten gibt (z. B. Menschen mit oder ohne Herzprobleme), wobei die für den Ausführenden relevantere Kategorie als Signal und die weniger relevante als Rauschen bezeichnet wird. Diese beiden Kategorien unterscheiden sich durch ihre Verteilung auf einer Evidenzskala, wobei die Signalverteilung einen höheren Mittelwert aufweist. So lässt sich nach dem Sammeln der Evidenz eine Klassifikation in Signal oder Rauschen festlegen. Dies führt zu einem der vier möglichen Ergebnissen:

Abbildung 2: Der obere Teil der Abbildung veranschaulicht die Annahme der Signaldetektionstheorie bei einer binären Entscheidungsaufgabe. Die drei vertikalen Linien stellen drei Entscheidungskriterien dar, die der Entscheidungsträger anwenden kann. Der untere Teil zeigt die vier möglichen FFTs, die erstellt werden können, wenn drei Merkmale in einer festen Reihenfolge herangezogen werden. Basierend auf den Klassifizierungen, auf die die ersten beiden Ausgänge hinweisen, werden die Bäume von links nach rechts FFTss, FFTsr, FFTrs und FFTrr genannt ("s" für Signal, "r" für Rauschen). Die Pfeile, die die Teile der Abbildung miteinander verbinden, zeigen die ungefähre Lage der Ausgangskriterien der vier FFTs an, wenn sie für eine binäre Signal/Rauschen-Klassifizierung verwendet werden. Von den vier FFTs ist FFTss am liberalsten und FFTrr am konservativsten. Die Entscheidungskriterien von FFTsr und FFTrs sind weniger extrem als die der anderen beiden, wobei FFTsr liberaler ist als FFTrs.

• Treffer (Signal wurde erkannt und ist die erwartete Antwort)
• korrekte Ablehnung (Rauschen wurde erkannt und ist die erwartete Antwort)
• Fehlschlag (Rauschen wurde erkannt, Signal wäre richtig gewesen)
• Fehlalarm (Signal wurde erkannt, Rauschen wäre richtig gewesen)

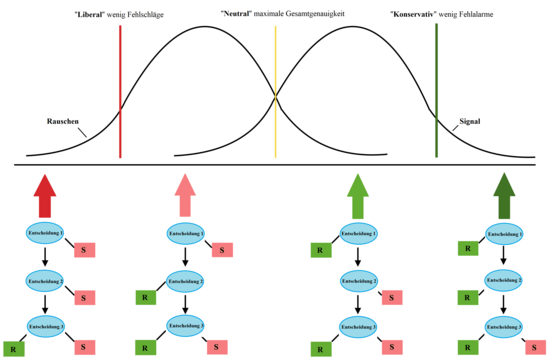
Um die Genauigkeit einer Klassifizierung zu maximieren, muss der Signalentdeckungstheorie zufolge das Klassifizierungskriterium, bei dessen Überschreitung ein Signal und bei dessen Unterschreitung ein Rauschen erkannt wird, auf der Evidenzskala sorgfältig ausgewählt werden. Dabei müssen die Kosten eines Fehlschlags (z. B. Patient mit Herzproblemen wird nicht ausreichend versorgt) mit den Kosten eines Fehlalarms (z. B. kardiologische Station wird durch falsch diagnostizierte Patienten überlastet) verglichen werden. Bei hohen Kosten durch Fehlschläge sollte das Kriterium niedrig (oder liberal) gewählt werden (d. h. eher links auf der Skala), während bei hohen Kosten bei Fehlalarmen das Kriterium hoch (oder konservativ) gewählt werden muss. Insgesamt ist damit eine Erkenntnis der Signalentdeckungstheorie, dass ein guter FFT im Vorhinein so erstellt werden muss, dass er für die jeweilige reale Situation ausreichend voreingenommen sein muss.

Aus der Untersuchung von FFTs aus der Sicht der Signalentdeckungstheorie aus dem Jahr 2011 von Luan, Schooler und Gigerenzer ergaben sich folgende Erkenntnisse:

Erstens wurde festgestellt, dass die Wahl der Ausgangsstruktur eines FFTs, also die Reihenfolge der Signal- und Rauschausgänge im Baum, der Festlegung der Entscheidungskriterien der Signalentscheidungen entspricht. Das bedeutet: Je früher sich im FFT ein Signalausgang befindet, desto liberaler ist der Baum. Betrachtet man also zwei FFTs, zeigt sich, dass sich die Kriterien der Bäume an dem Ausgang unterscheiden, an dem die Bäume zum ersten Mal zu unterschiedlichen Klassifizierungen kommen. So ist der Baum, welcher zuerst einen Signalausgang besitzt, immer liberaler als der Baum mit einem Rauschausgang. Dieses Prinzip bezeichnet man als "lexikografische Verzerrung" von FFTs.

Zweitens stellte man durch Simulationen fest, dass die Wahl der Ausgangsstrukturen einen drastischen Einfluss auf die Erwartungswerte einer Entscheidung haben kann, falls sich die Konsequenzen von Fehlalarmen und Fehlschlägen unterscheiden. Das verdeutlicht, dass die Konstruktion und Ausführung auf diese Kriterien angepasst sein muss.

Drittens ist die Gesamtempfindlichkeit eines FFTs, d. h. wie gut ein Baum ein Signal von einem Rauschen unterscheiden kann (gemessen mit d' oder A' in der Signalentdeckungstheorie), von den Eigenschaften der Knoten abhängig, aber nicht wesentlich von der Ausgangsstruktur des Baums.

Zuletzt wurde beobachtet, dass die Leistung eines FFTs robust und vergleichbar mit anspruchsvolleren in der Signalentdeckungstheorie entwickelten Entscheidungsalgorithmen ist, einschließlich des idealen Beobachteranalysemodells und des optimalen sequenzieller Stichprobeverfahrens. Es stellte sich zudem heraus, dass FFTs beim Klassifizieren von Testdaten im Vergleich mit anderen Modellen am besten abschnitten, wenn wenig Trainingsdaten vorliegen (z. B. weniger als 80 Trainingsdatensätze).

Einsatzgebiete

Medizin

Aufgrund ihrer Übersichtlichkeit finden FFTs in der Medizin dort Einsatz, wo wenig medizinisches Vorwissen vorhanden ist oder benötigt wird. Beispielsweise als Entscheidungshilfen für Patienten, ob es anhand von beobachteten Symptomen an der Zeit ist, einen Arzt aufzusuchen.

FFTs werden auch verwendet, um klinischem Personal zu helfen, Entscheidungen über die Behandlung von Patienten zu treffen. So gibt es unter anderem FFTs, die dabei helfen können, zu entscheiden, ob ein Patient eine klinisch relevante depressive Stimmung vorweist oder ob ein Patient anhand von Testwerten unter kardiologische Beobachtung gestellt werden sollte.

Militär

Abbildung 3: Ein FFT, der Soldaten dabei hilft einzuordnen, ob es sich bei einem annähernden Fahrzeug um einen Selbstmordattentäter handelt.

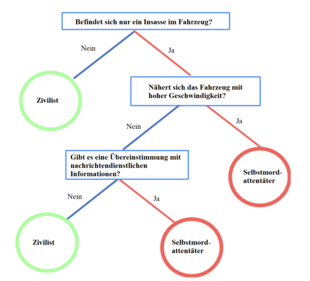
Das Militär ließ eigene FFTs entwickeln, welche sich auf akute Einsatzszenarien beziehen. Dabei handelte es sich unter anderem um Szenarien, wie etwa ob es sich bei einem annähernden Fahrzeug um einen Suizidattentäter handelt oder wie man bei Konvoifahrten eine Straßenkreuzung sichert. Es wurde dabei festgestellt, dass FFTs vergleichbar akkurat wie komplexere, bewährte Systeme sind.

Verwaltung

In einer Studie von Luan und Reb aus dem Jahr 2017 wurden verschiedene Entscheidungsmodelle, darunter FFTs, darauf untersucht, wie diese Entscheidungsprozesse von Probanden im Bezug auf die Wahlmöglichkeiten und die Reaktionszeiten beschreiben können. Die Probanden sollten, ohne vorher von den Modellen zu wissen, leistungsbezogene Personalfragen ("Bonuszahlung" oder "Entlassung") beantworten. Dabei stellte man fest, dass eine signifikant große Anzahl von Probanden dabei intuitiv FFTs, bzw. FFT-ähnliche Strukturen anwandten und dabei auch auf Änderungen der Verteilung der geforderten Ergebnisse (also dem Verhältnis von Bonuszahlungen und Entlassungen) durch Anpassung der Knoten adaptiv reagierten.

Illustrativ gibt es auch einen FFT, mit dem entschieden werden kann, ob man für eine Klassifizierung einen FFT in Betracht ziehen sollte.

Informatik

In der künstlichen Intelligenz sind FFTs ein mögliches Modell, um binäre Klassifikationen durchzuführen. Mit ihnen kann untersucht werden, welche Merkmale bei der Bestimmung des Ergebnisses einer Klassifizierungsaufgabe am wichtigsten sind oder welche Eingabeparameter die stärkste Gewichtung auf das Resultat haben.

2017 stellten Phillips, Neth, Woike und Gaissmaier das R-Paket FFTrees vor, welches eine Anwendung ist, um FFTs zu konstruieren, grafisch darzustellen und auszuwerten.

Vor- und Nachteile

Vorteile

Ein Vorteil von FFTs ist ihre geringe Komplexität und damit folgend schnelle Ausführbarkeit. Da sich auf jeder Ebene des FFTs maximal je eine Frage und zwei Ausgänge befinden, können sie deutlich schneller als andere Entscheidungsbäume abgearbeitet werden. So hat ein FFT mit vier Ebenen drei Fragen mit vier Ausgängen, während ein voll besetzter binärer Entscheidungsbaum der gleichen Größe sieben Fragen und acht Ausgänge besitzt.

FFTs sind resistenter gegen das aus der Statistik bekannte Problem der Überanpassung als beispielsweise Regressionsmodelle und führen dabei zu ähnlich guten Ergebnissen. Das Problem der Überanpassung ist, dass ein Modell zu sehr an seine Trainingsdaten gewöhnt ist und so bei neuen, ungewohnten Daten zu Fehlklassifikationen neigt.

Außerdem sind FFTs mit der menschlichen Entscheidungsfindung gut zu vereinbaren: FFTs erlauben es, gezielt große Datenmengen auszublenden und so anhand nur weniger Daten, welche dann aber tatsächlich relevant sind, Entscheidungen zu treffen.

Nachteile

Ein Nachteil der FFTs besteht darin, dass dem Anwender der FFT, durch das Herunterbrechen komplexer Themen auf wenige Fragen, zu simpel vorkommt und dem Ergebnis des Models damit weniger Vertrauen geschenkt wird.

Mit FFTs lassen sich generell nur binäre Klassifizierungen darstellen, d. h. es gibt nur zwei mögliche Resultate. Dementsprechend sind FFTs in Bereichen ungeeignet, die mehr als zwei Resultate benötigen bzw. in denen mehr als zwei Resultate berücksichtigt werden sollten. So könnte beispielsweise mit einem FFT zwar entschieden werden, ob ein Patient kardiologische Behandlung benötigt, es kann aber keine Aussage über die Notwendigkeit einer gleichzeitig notwendigen neurologischen Behandlung getroffen werden.

Außerdem kann beobachtet werden, dass Anwender eher dazu neigen, Modelle zu nutzen, welche viele Informationen verwenden, um zu ihren Ergebnissen zu kommen.

Zuletzt spricht gegen FFTs ihre geringe Popularität und ein daraus mangelndes Angebot von FFTs in Standardsoftware.