Schrödingers Katze

Schrödingers Katze im Kasten: Tot? Lebendig? Sowohl als auch?

Schrödingers Katze bezeichnet ein populär gewordenes Gedankenexperiment aus der Anfangszeit der Modernen Physik. Erwin Schrödinger verdeutlichte damit 1935, dass die neuen Vorstellungen vom Zustand eines Teilchens, die die Grundlage der bis heute erfolgreichen Quantenmechanik bilden, „einfach falsch“ werden, wenn man sie auf „grob tastbare und sichtbare Dinge“ bezieht.

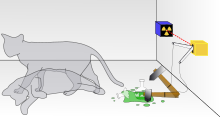
In der Quantenmechanik muss man sich vorstellen, dass der Zustand eines punktförmigen Elektrons einer Welle ähneln kann, die im Raum über einen mehr oder weniger großen Bereich ausgedehnt ist (Welle-Teilchen-Dualismus). Zum Beispiel ist ein Elektron im Atom nicht nur an einem Punkt, sondern gleichzeitig in „verwaschener“ Weise auch an jedem anderen Punkt im ganzen Atom anwesend. So ein Zustand wird genauer als kohärente Superposition von solchen Zuständen bezeichnet, in denen das Elektron tatsächlich nur einen Ort hat. Ebenso muss man sich von einem radioaktiven Atom vorstellen, dass es nach Ablauf einer Halbwertzeit einen Superpositionszustand einnimmt, in dem es zu gleichen Teilen sowohl „zerfallen“ als auch „nicht zerfallen“ ist. Analog müsste man sich dann auch von einer Katze vorstellen können, dass sie in kohärenter Superposition gleichzeitig im Zustand lebendig und im Zustand tot ist. Um zu illustrieren, wie sie in diesen Zustand kommen kann, lässt Schrödinger in einem „burlesk ausgeschmückten“ Gedankenexperiment die kohärente Superposition von einem radioaktiven Atom auf eine Katze übergehen. Die Katze ist in einer Stahlkammer eingesperrt, zusammen mit einer „Höllenmaschine“ bestehend aus dem radioaktiven Atom, einem Geigerzähler, einem Hämmerchen und einem Fläschchen voll Giftgas. Das Giftgas tötet die Katze, sobald die Strahlung des Atoms über den Geigerzähler einen Schlag mit dem Hämmerchen auslöst, der das Fläschchen zertrümmert. Zu Beginn lebt die Katze, aber im Laufe einer Halbwertzeit gerät das Atom in den genannten kohärenten Superpositionzustand aus den Zuständen „zerfallen“ und „nicht zerfallen“. Entsprechend müsse die Katze dann in einen genauso „verwaschenen“ Zustand geraten, in dem sie je zur Hälfte sowohl „tot“ als auch gleichzeitig „lebendig“ ist. In diesem Superpositionszustand müsste die Katze bleiben, bis er durch eine wirkliche Beobachtung beendet wird. Diese würde keinen Überlagerungszustand feststellen, sondern entweder das Ergebnis „tot“ oder „lebendig“, nach einer Halbwertzeit also mit je 50 % Wahrscheinlichkeit.

Der deutliche Gegensatz zwischen dieser Vorstellung von einem „verwaschenen“ Zustand einer Katze und der gesicherten Anschauung hat innerhalb wie außerhalb der Physik jahrzehntelange Diskussionen angeregt. Zum Teil haben sie sich von Schrödingers ursprünglicher Darstellung auch erheblich entfernt. Im physikalischen Sinn ist das Problem spätestens seit den 1980er Jahren durch die Theorie der quantenmechanischen Dekohärenz geklärt worden. Demnach kann ein in Schrödingers Sinn „verwaschener“ Zustand einer Katze höchstens für eine unmessbar kurze Zeitspanne existieren, um dann in eine Situation überzugehen, die man sich schon in der klassischen Physik und sogar im Alltag mühelos vorstellen kann, wenn nämlich z. B. nach einem Münzwurf der Zustand der Münze unklar bleibt, bis jemand hinguckt und entweder „Kopf“ oder „Zahl“ feststellt.

Dabei ist es wichtig, dass es sich bei der Katze um ein komplexes makroskopisches System handelt. Dessen ungeachtet spricht man in Anlehnung an Schrödingers Gedankenexperiment zuweilen auch bei einem mikroskopischen quantenmechanischen System von einem Katzenzustand, wenn man verschiedene seiner Zustände kohärent überlagert hat und dieser kohärente Überlagerungszustand anhält, bis das System durch eine Messung auf einen von ihnen festgelegt wird.

Detailliertere Erklärung

Dieses Kapitel gibt eine detailliertere Erklärung in möglichst leicht zugänglich gehaltener Form. Auf manche Einzelheiten wird zunächst verzichtet. Eine genaue Darstellung ist vor allem in den entsprechend verlinkten Hauptartikeln zu finden.

Superpositionsprinzip der Quantenmechanik

Das Superpositionsprinzip der Quantenmechanik drückt aus, dass zwei Zustände eines Quantensystems sich so addieren lassen wie zwei Wellenfelder oder zwei Vektoren, und dass die Summe einen neuen Zustand (bzw. Wellenfeld oder Vektor) darstellt. In dem Superpositionszustand sind beide Ausgangszustände als Komponenten in derselben Weise präsent, wie es zwei Vektoren, die man addiert, in dem resultierenden Vektor sind (vgl. etwa Kräfteparallelogramm). Vor dem Addieren können sie noch mit Faktoren versehen werden, weshalb die Superposition auch als Linearkombination bezeichnet wird. Bei der quantenmechanischen Superposition sind die Faktoren komplexe Zahlen und werden auch Amplituden genannt, denn ihre Betragsquadrate geben an, wie stark die Ausgangszustände im Superpositionszustand vertreten sind. Die Linearkombination heißt genauer auch kohärente Überlagerung, weil es nicht nur von den Absolutbeträgen der Faktoren abhängt, welchen physikalischen Zustand das System einnimmt, sondern auch von ihren komplexen Phasen.

Zwei Beispiele:

• Doppelspaltversuch: Wenn ein Elektron durch eine Blende mit einem Schlitz fliegt und auf einem Leuchtschirm nachgewiesen wird, dann hat es dort vor dem Nachweis eine ausgedehnte Wellenfunktion $\psi _{1}({\vec {r}})$. Das Elektron wird nur an einem einzigen Ort ${\vec {r}}$ nachgewiesen, und die Wahrscheinlichkeit, dass es der Ort ${\vec {r}}$ ist, wird durch das Betragsquadrat $|\psi _{1}({\vec {r}})|^{2}$ gegeben. Viele nacheinander registrierte Elektronen zusammen zeigen dann auf dem Schirm die Intensitätsverteilung $|\psi _{1}({\vec {r}})|^{2}$. Fliegen Elektronen durch einen benachbarten Schlitz, dann haben sie eine andere Wellenfunktion $\psi _{2}({\vec {r}})$ und zeigen die Intensitätsverteilung $|\psi _{2}({\vec {r}})|^{2}$. Ist abwechselnd nur der eine oder der andere Schlitz offen, zeigt sich die Summe beider Intensitätverteilungen

$|\psi _{1}({\vec {r}})|^{2}+|\psi _{2}({\vec {r}})|^{2}$.

Dies ist das Ergebnis einer inkohärenten Überlagerung.

Sind aber beide Schlitze gleichzeitig offen, kann jedes Elektron durch jeden von ihnen zum Schirm gelangt sein und hat als Wellenfunktion die kohärente Überlagerung der beiden einzelnen Wellenfunktionen: $\Psi ({\vec {r}})=\psi _{1}({\vec {r}})+\psi _{2}({\vec {r}})$. Deren Betragsquadrat

$|\Psi ({\vec {r}})|^{2}=|\psi _{1}({\vec {r}})|^{2}+|\psi _{2}({\vec {r}})|^{2}+2|\psi _{1}({\vec {r}})|\;|\psi _{2}({\vec {r}})|\,\cos \gamma ({\vec {r}})$

gibt wieder die Wahrscheinlichkeit an, dass das Elektron am Ort ${\vec {r}}$ auftrifft. Sie unterscheidet sich vom Fall der inkohärenten Überlagerung durch den Interferenzterm, der außer von den beiden Amplituden auch vom Winkel $\gamma ({\vec {r}})$ abhängt, das ist die Differenz der komplexen Phasen von $\psi _{1}({\vec {r}})$ und $\psi _{2}({\vec {r}})$ am Ort ${\vec {r}}$ des Schirms. Abhängig von $\cos \gamma ({\vec {r}})$ kann die Intensität daher kleiner, aber auch größer sein, als wenn bei allen Elektronen immer entweder der eine oder der andere Schlitz geschlossen gewesen wäre. $\gamma ({\vec {r}})$ variiert von Ort zu Ort. Genau dies erklärt die Interferenzstreifen, die sich auf dem Schirm bilden, wenn beide Schlitze dauernd offen sind und man viele Elektronen nacheinander auftreffen lässt. Die Interferenz zeigt, dass man bei jedem einzelnen Elektron annehmen muss, es habe beim Auftreffen beide Zustände $\psi _{1}({\vec {r}})$ und $\psi _{2}({\vec {r}})$ inne.

• Spin: Der Elektronenspin hat (in Bra-Ket-Notation) die beiden Zustände $|\!+\!z\rangle$ und $|\!-\!z\rangle$, in denen er parallel bzw. antiparallel zur z-Achse ausgerichtet ist. Der kohärente Superpositionszustand $|\!+\!x\rangle =\alpha (\;|\!+\!z\rangle +|\!-\!z\rangle )$ (mit gleichen Amplituden $\alpha ={\sqrt {\tfrac {1}{2}}}$, also auch gleichen Wahrscheinlichkeiten $|\alpha |^{2}={\tfrac {1}{2}}$, und mit Phasendifferenz $\gamma =0$) ist dann der Zustand mit Ausrichtung parallel zur x-Achse. Wenn man nur die Phasendifferenz ändert und z. B. $\gamma =\pi /2$ wählt, ist die kohärente Überlagerung $|\!+\!y\rangle =\alpha |\!+\!z\rangle +\alpha e^{i\pi /2}|\!-\!z\rangle =\alpha (|\!+\!z\rangle -|\!-\!z\rangle )$ eine andere, denn sie beschreibt den Zustand mit Ausrichtung zur y-Achse.

Wenn ein Zustand sich zeitlich verändert, geschieht das nach der grundlegenden Bewegungsgleichung der Quantenmechanik (Schrödingergleichung) dadurch, dass ein anderer Zustand mit ihm superponiert wird, wobei dessen Amplitude vom Wert Null an zeitlich anwächst. Kohärente Superpositionen entstehen daher zwangsläufig bei jeder Veränderung eines Anfangszustands.

Bei einem radioaktiven Atom, das ein hochenergetisches Alphateilchen emittieren kann, ist im Anfangszustand das Alphateilchen noch mit dem Atomkern verschmolzen. Diesem Zustand wird mit zeitlich allmählich anwachsender Amplitude ein Zustand superponiert, in dem sich das Alphateilchen von dem Rest des Atomkerns (dem „Tochterkern“) entfernt. Gleichzeitig reduziert sich in der Superposition der Beitrag des Anfangszustands, so dass das Betragsquadrat seiner Amplitude vom Anfangswert 1 aus gemäß dem exponentiellen Zerfallsgesetz $e^{-\lambda t}$ abnimmt (die radioaktive Halbwertszeit ist $T_{1/2}\approx {\tfrac {0{,}693}{\lambda }}$). Der Atomkern befindet sich dann in einem kohärenten Überlagerungszustand der beiden Zustände „zerfallen“ und „nicht zerfallen“.

Wahrscheinlichkeitsdeutung der Quantenmechanik

Eine physikalische Größe hat in einem bestimmten Zustand eines Quantensystems im Allgemeinen keinen bestimmten Wert, denn bei wiederholten identischen Messungen an gleichen Quantensystemen zeigt sich diese Größe mit verschiedenen Werten. Ausgenommen sind nur bestimmte Zustände des Systems, nämlich die speziell zu dieser physikalischen Größe gehörenden Eigenzustände. Die betreffenden Messwerte sind die Eigenwerte dieser Größe. Ein jeder beliebige Zustand des Systems ist eine geeignete kohärente Superposition der Eigenzustände einer beliebig gewählten messbaren Größe. Dabei gibt das Betragsquadrat der Amplitude, mit der ein bestimmter Eigenzustand in dieser Superposition vorkommt, die Wahrscheinlichkeit an, mit der sich bei einer Messung der zugehörige Eigenwert der gewählten Größe zeigt. Als Beispiel wurde oben eine beliebige Wellenfunktion $\psi ({\vec {r}})$ als kohärente Superposition der Ortseigenzustände genannt, bei denen der Ort des Elektrons eindeutig festliegt.

Dies gilt nicht nur für zahlenmäßige Messwerte, sondern auch für andere beobachtbare Eigenschaften, beim Atom z. B. für die Beobachtung „zerfallen oder nicht?“ mit den beiden entsprechenden Eigenzuständen „zerfallen“ bzw. „nicht zerfallen“. Die mit der Zeit exponentiell abnehmende Wahrscheinlichkeit, das Atom unzerfallen vorzufinden, drückt sich im Experiment darin aus, dass von einer anfangs großen Anzahl gleicher Atome nach einer Zeit $t$ ein Bruchteil $e^{-\lambda t}$ noch unverändert vorzufinden ist, nach einer Halbwertszeit $T_{1/2}$ also genau die Hälfte. Dies ist die exakte Vorhersage eines in zahllosen Experimenten bestätigten reproduzierbaren Messergebnisses. Ob aber ein einzelnes herausgegriffenes Atom zu einem bestimmten Zeitpunkt zerfallen sein wird, ist unmöglich vorherzusagen. Diese Frage kann nur dadurch entschieden werden, dass man es zu diesem Zeitpunkt beobachtet, und muss bis dahin offen bleiben.

Kohärente Überlagerung ist reversibel

Wenn ein Anfangszustand sich gemäß der Schrödingergleichung in eine kohärente Überlagerung mit anderen Zuständen entwickelt, dann ist das ein umkehrbarer („reversibler“) Vorgang. Die Reversibilität ist nicht nur theoretisch möglich, sondern wird z. B. technisch vielfach angewendet, etwa bei der Manipulation der Kernspins in der medizinischen MRT-Diagnostik. Daher deutete das Paradoxon, dass Schrödingers Katze in den „verwaschenen“ Überlagerungszustand aus „tot“ und „lebendig“ gerät, auf das weitere Paradoxon hin, dass es nach den Regeln der Quantenmechanik (mindestens theoretisch) möglich sein müsste, die Katze aus diesem Zustand heraus wieder ganz lebendig zu machen, sogar unabhängig davon, wie gering die Amplitude für die Komponente „lebendig“ schon geworden wäre. Voraussetzung für die Reversibilität ist, dass die komplexen Phasen der Amplituden von keinen zufälligen Störungen verändert werden. Solche Störungen z. B. bei Qbits zu verhindern, ist die größte technische Hürde bei der Verwirklichung von Quantencomputern. Für eine Katze in normaler Umgebung kann man ausschließen, dass sie von solchen Störungen frei ist.

Beim Zerfall des Atoms in Schrödingers Gedankenexperiment tritt als zweite Komplikation auf, dass es für die Superposition mit dem Anfangszustand genau genommen nicht nur einen bestimmten Zustand nach dem Zerfall gibt, sondern unendlich viele. Sie unterscheiden sich in der genauen Aufteilung der Energie im Rahmen der natürlichen Linienbreite.

Beide Effekte machen die Reversibilität des Gedankenexperiments zunichte, werden aber von Schrödinger nicht angesprochen. Er geht vielmehr davon aus, dass die kohärente Superposition bis zum Moment der Beobachtung beim Öffnen der Stahlkammer anhält.

Dekohärenz

In den 1980er Jahren wurde innerhalb der Quantenmechanik die Dekohärenztheorie entwickelt. Darin wird die Umgebung des Beobachtungsobjekts in die quantenmechanische Beschreibung mit einbezogen. Demnach entsteht der paradox erscheinende kohärente Überlagerungszustand anfangs tatsächlich, bleibt aber nur solange bestehen, wie das System nahezu perfekt von Umgebungseinflüssen abgeschirmt ist. Aus jüngerer Zeit gibt es Beispiele dafür aus realen physikalischen Experimenten: Etwa ein einzelnes Teilchen in einer Atom- oder Ionenfalle, ein Qbit oder in gewissen Fällen messbare Ströme in Supraleitern. Aber bei Schrödingers Gedankenexperiment sagt die Quantenmechanik weder für das zerfallende Atom noch für die Katze nach einer Stunde den kohärent überlagerten Zustand „Atom ist sowohl zerfallen als auch nicht zerfallen“ bzw. „Katze ist sowohl tot als auch lebendig“ vorher, sondern den Zustand „Atom ist entweder zerfallen oder nicht“ bzw. die „Katze ist entweder tot oder lebendig“. Denn immer wenn ein anfänglich im kohärenten Überlagerungszustand befindliches Objekt mit einer makroskopischen Umgebung in Wechselwirkung steht – wie das vom Atom emittierte Teilchen mit dem Füllgas des Geigerzählers oder die Katze mit ihrer Atemluft und beide mit der Wärmestrahlung etc. –, gehen die stabilen Phasenbeziehungen in unmessbar kurzer Zeit verloren. Der Zustand des Objekts geht damit in eine inkohärente Überlagerung über, die auch als Zustandsgemisch bezeichnet wird (früher auch als Gemenge). In Objekten der Größe einer Katze geschieht das in einer Umgebung bei Normalbedingungen in unmessbar kurzer Zeit, Abschätzungen ergeben z. B. 10⁻³⁰s. Danach sind irgendwelche Folgen der ehemaligen Kohärenz der Überlagerung aber nicht mehr zu beobachten. Der Zustand der Katze muss dann so beschrieben werden wie z. B. der eingangs erwähnte Zustand der Münze nach dem Münzwurf, nämlich als unbestimmt – bis jemand hinguckt und entweder „Kopf“ oder „Zahl“ oder, im Falle der Katze, „tot“ oder „lebendig“ feststellt. Der Zustand des Würfels vor dem Aufheben des Würfelbechers ist ein anderes Beispiel. Es treten keine der für die Quantenmechanik charakteristischen kombinierten Wirkungen („Interferenzen“) mehr auf, für deren Entstehen das Objekt zwei überlagerte Zustände gleichzeitig innehaben müsste. Man darf annehmen, das Objekt befinde sich in einem wohlbestimmten und nicht „verwaschenen“ Zustand, man könne nur nicht vorhersagen, in welchem von mehreren möglichen Zuständen man es bei der Beobachtung vorfinden wird. Damit hat der für die Katze vorhergesagte Zustand in der Realität nichts sonderbares mehr an sich. Vielmehr ist die quantenmechanische Vorhersage für den Zustand der Katze mit der Anschauung ebenso verträglich wie die ganz ähnlichen Aussagen der klassischen Physik.

Es besteht allerdings der Unterschied, dass es in der Quantenmechanik notwendig sein kann, einen Zustand in Form eines solchen inkohärenten Gemischs schon bei der Beschreibung eines einzigen Objekts anzusetzen, auch wenn dessen Vorgeschichte und sein Anfangszustand mit der theoretisch größten denkbaren Präzision bekannt sind (siehe irreversible Umwandlung in ein Zustandsgemisch bei der quantenmechanischen Messung). In der klassischen Statistischen Physik muss man das hingegen nur, wenn das betrachtete Objekt aus einer großen Zahl gleicher Objekte in ähnlichen Zuständen zufällig herausgegriffen wurde (wie ein Molekül aus einem Gas) oder sein Anfangszustand und die Vorgeschichte nicht mit mathematischer Präzision bekannt sind (wie beim Würfel oder der Münze). Dieser Unterschied spielt für die Praxis aber keine Rolle, denn die einzigen durch empirische Überprüfung beobachtbaren Größen sind in beiden Fällen die prozentualen Anteile der verschiedenen Zustände im inkohärenten Gemisch, und solche Messungen erfordern in beiden Fällen eine lange Reihe von Wiederholungsmessungen an vielen Objekten im gleichen Zustand.

Inkohärente Überlagerung ist irreversibel

Ein Zustandsgemisch kann in der Quantenmechanik nicht durch eine Wellenfunktion oder einen Zustandsvektor mathematisch dargestellt werden, man braucht stattdessen einen Dichteoperator (oder Dichtematrix). Im Zustandsgemisch (aus beispielsweise zwei inkohärent überlagerten Zuständen) darf man das Quantenobjekt so behandeln, als ob es mit einer bestimmten Wahrscheinlichkeit $p_{1}$ entweder in dem einen der beiden Zustände sei, oder mit der Wahrscheinlichkeit $p_{2}=1-p_{1}$ in dem anderen. Phasenfaktoren oder Interferenzterme tauchen nicht mehr auf. Falls das Zustandsgemisch aus einem kohärenten Superpositionszustand hervorgegangen ist, sind $p_{1}$ und $p_{2}$ die Betragsquadrate der Amplituden, mit denen die beiden Zustände vor der Dekohärenz kohärent überlagert gewesen waren. So ein Zustandsgemisch entspricht daher in allen beobachtbaren Konsequenzen dem aus der klassischen Physik (und dem Alltag) bekannten Fall der unvollständigen Kenntnis, welcher der beiden möglichen Zustände denn nun vorliegt. Der Zustand des Systems „Katze mit Höllenmaschine“ ist nach kürzester Zeit analog zum Zustand einer Münze nach einem Münzwurf, bevor jemand durch Beobachtung feststellt, ob sie Kopf oder Zahl zeigt.

Schrödinger drückt sich hierzu in seiner Veröffentlichung nicht klar aus. An anderer Stelle jedoch bezeichnet er diese klassisch interpretierbare Art der Unbestimmtheit als "Boltzmannisch", in Erinnerung an die Leistungen Ludwig Boltzmanns in der Entwicklung der klassischen statistischen Mechanik. Dagegen sei es ihm bei seinem Gedankenexperiment darum gegangen, die paradox erscheinenden Konsequenzen einer "Heisenbergischen" Unbestimmtheit zu demonstrieren. Diese tritt nur bei der kohärenten Superposition auf und drückt sich auch in der Heisenbergschen Unschärferelation aus.

Die Irreversibilität des Übergangs in eine inkohärente Mischung kommt auch darin zum Ausdruck, dass die Entropie zunimmt. Ein Zustand, der durch eine Wellenfunktion oder einen Zustandsvektor genau beschrieben ist (reiner Zustand, auch ein kohärenter Superpositionszustand ist ein reiner Zustand), hat immer die Entropie $S=0$. Die Entropie eines Gemischs (aus mindestens zwei Zuständen) dagegen ist immer größer als Null.

Beziehung zum Messprozess

Eine Messung ist in der klassischen Physik die Feststellung des am Messobjekt eindeutig schon vorhandenen Werts einer Größe. In der Quantenmechanik aber haben die Messobjekte vor der Messung meist noch gar keinen bestimmten Wert. Vielmehr wird dieser – auf eine zufällige, bisher nicht weiter aufgeklärte Weise – unter den verschiedenen möglichen Werten durch die Messung erst ausgewählt. Schrödinger definiert für die Quantenmechanik den Begriff Messung daher neu und rückt die Reproduzierbarkeit des Messwerts ins Zentrum:

„Die planmäßig herbeigeführte Wechselwirkung zweier Systeme (Meßobjekt und Meßinstrument) heißt eine Messung an dem ersten System, wenn sich ein direkt sinnenfälliges variables Merkmal des zweiten (Zeigerstellung) bei sofortiger Wiederholung des Vorganges (an demselben Meßobjekt, das inzwischen keinen anderweitigen Einflüssen ausgesetzt worden sein darf) stets innerhalb gewisser Fehlergrenzen reproduziert.“

– Erwin Schrödinger

In diesem Sinn gilt die Wahrnehmung, die der Beobachter beim Öffnen der Stahlkammer vom Zustand der Katze gewinnt, als Messung. Auf Schrödingers Katze wurde daher häufig Bezug genommen, wenn die bisher ungeklärte Problematik des Zufälligen beim quantenmechanischen Messprozesses diskutiert wurde. Daraus ist jedoch nicht zu schließen, dass es in der realen Welt bis zum Moment der Wahrnehmung durch den Beobachter unbestimmt geblieben ist, ob das Atom zerfallen ist oder nicht, und schrittweise weiter bis zur Frage, ob die Katze tot ist oder lebendig. Denn das Ergebnis steht schon mit jeder irreversiblen makroskopischen Reaktion fest, die von dem Zerfall ausgelöst wird. Das kann z. B. schon die Ionisationsspur des Alphateilchens im Gas des Geigerzählers sein und ist auf jeden Fall längst abgeschlossen, bevor die Katze überhaupt das Giftgas einatmet.

Diese Interpretation stützt sich wesentlich auf die Dekohärenz-Theorie, die ab den 1970er Jahren entwickelt wurde. Vorher wurden noch Ansichten vertreten, in denen die verschiedenen kohärent überlagerten Zustände des Messobjekts bis zum Moment der Messung, bei der Katze also bis zur Beobachtung beim Öffnen der Stahlkammer, als wirklich angesehen wurden. Eugene Wigner, ein weiterer Mitbegründer der Quantenmechanik, spitzte diese Ansicht dahingehend zu, dass eine Messung erst mit dem bewussten Wahrnehmen des Ergebnisses beendet ist, und illustrierte dies 1961 durch ein Gedankenexperiment, das als Wigners Freund bekannt wurde. Das entspricht dem Fall, dass die Stahlkammer von einem Menschen geöffnet wird, der nicht begreift, was er sieht. Dann soll die Katze noch solange im Überlagerungszustand verbleiben, bis ein befreundeter Physiker über den Anblick informiert wird und das Ergebnis feststellt. Dagegen wurde es von philosophischer Seite als absurd angesehen, dass menschliche Beobachtung aktuell darüber zu entscheiden hätte, was existiert und was nicht. Nach der Entwicklung der Dekohärenztheorie zog Wigner seinen Gedanken zurück.^{[Beleg suchen]}

Rezeption und Interpretationen des Gedankenexperiments

Langsame Rezeption und anhaltende Diskussion

Schrödingers Gedankenexperiment wurde in den ersten 20 Jahren weder in der fachphysikalischen noch von der populärwissenschaftlichen Literatur beachtet. Eine erste Erwähnung überhaupt sieht der Wissenschaftshistoriker Robert P. Crease in einem Beitrag von 1957 des unorthodoxen Philosophen Paul Feyerabend zu einer Debatte über die Bedeutung der Wellenfunktion. Ab den 1970er Jahren erschien das Gedankenexperiment in Texten der Science-Fiction. Jedoch schon 1980 konnte der Physiker Anthony J. Leggett in einer Grundlagenarbeit über die Rolle makroskopischer Systeme bei quantenmechanischen Messungen Schrödingers Katze als eine der berühmtesten Paradoxien der Grundlagen der Quantenmechanik bezeichnen. Heute wird Schrödingers Katze in einer populären Liste als zweitwichtigstes Gedankenexperiment überhaupt gezählt. Die Diskussion in der Fachwelt hält bis in die jüngste Zeit an (siehe z. B. Ref.).

Unabhängig von der Dekohärenztheorie werden die Abläufe im hypothetischen perfekt verschlossenen Kasten in den verschiedenen Schulen und Deutungen der Quantenmechanik sehr unterschiedlich interpretiert.

Schrödingers Deutung: Wellenfunktion liefert kein Abbild der Realität, sondern einen Katalog von zu erwartenden Messergebnissen

Schrödinger sah es (wie u. a. auch Einstein) als sehr problematisch an, dass die neuen Begriffsbildungen der 1927 von Bohr und Heisenberg vorgestellten Kopenhagener Deutung der Quantenmechanik mit der Anschauung nicht mehr so zu verbinden waren wie von den Begriffen, Theorien und Modellen der klassischen Physik her gewohnt. Schon als er 1926 die Wellenmechanik geschaffen hatte, strebte er nach einer Interpretation, in der die Atomphysik eher die Anschaulichkeit und Determiniertheit der klassischen Physik bewahren könnte. Unter dem Titel „Die gegenwärtige Situation in der Quantenmechanik.“ schrieb er 1935 die kritische Abhandlung, in der er die Probleme herausarbeitete und durch das Gedankenexperiment mit der Katze veranschaulichte. Nach der Kopenhagener Deutung gibt die Wellenfunktion (oder der Zustandsvektor) die vollständigste Beschreibung eines physikalischen Objekts, die die Natur erlaubt. Die Unbestimmtheiten der Werte von konjugierten Größen (wie Ort und Impuls), wie sie z. B. auch durch die Heisenbergsche Unbestimmtheitsrelation festgestellt werden, sind dann als naturgegeben hinzunehmen. Sie beruhen nicht wie in der klassischen Physik auf einer mangelhaften Kenntnis vom genauen Zustand eines Objekts, z. B. eines einzelnen Moleküls in der kinetischen Gastheorie (nach Boltzmann). Schrödinger bezeichnet die fundamental neue quantenmechanische Unbestimmtheit als Verwaschenheit und nennt sie an anderer Stelle Heisenbergisch im Gegensatz zur klassischen Boltzmannischen Unbestimmtheit.

Er bezeichnete diese Interpretation als „aus Bedrängnis geboren“ und wollte sie nicht akzeptieren. Insbesondere solle die Wellenfunktion nicht als Abbild oder Modell der Realität angesehen werden. Um diese Mängel in grotesker Weise zu demonstrieren, konstruierte er das folgende Gedankenexperiment:

„Man kann auch ganz burleske Fälle konstruieren. Eine Katze wird in eine Stahlkammer gesperrt, zusammen mit folgender Höllenmaschine (die man gegen den direkten Zugriff der Katze sichern muß): in einem Geigerschen Zählrohr befindet sich eine winzige Menge radioaktiver Substanz, so wenig, daß im Laufe einer Stunde vielleicht eines von den Atomen zerfällt, ebenso wahrscheinlich aber auch keines; geschieht es, so spricht das Zählrohr an und betätigt über ein Relais ein Hämmerchen, das ein Kölbchen mit Blausäure zertrümmert. Hat man dieses ganze System eine Stunde lang sich selbst überlassen, so wird man sich sagen, daß die Katze noch lebt, wenn inzwischen kein Atom zerfallen ist. Der erste Atomzerfall würde sie vergiftet haben. Die Psi-Funktion des ganzen Systems würde das so zum Ausdruck bringen, daß in ihr die lebende und die tote Katze (s.v.v.) zu gleichen Teilen gemischt oder verschmiert sind. Das Typische an solchen Fällen ist, daß eine ursprünglich auf den Atombereich beschränkte Unbestimmtheit sich in grobsinnliche Unbestimmtheit umsetzt, die sich dann durch direkte Beobachtung entscheiden läßt. Das hindert uns, in so naiver Weise ein „verwaschenes Modell“ als Abbild der Wirklichkeit gelten zu lassen.“

– Erwin Schrödinger

Schrödinger diskutiert dann dieses Gedankenexperiment gar nicht weiter. Für ihn stellt sich die physikalische Frage nach der Bedeutung der „Verwaschenheit“ ohnehin in gleicher Weise schon beim Anfangszustand des Alphateilchens, bevor es den Atomkern verlässt, und alle weiteren „burlesken“ Ausschmückungen mit der Katze sind physikalisch irrelevant.

In der Abhandlung von 1935 arbeitet Schrödinger im Weiteren die Begriffe der Verschränkung, der Messung und der Zustandsreduktion heraus. Dabei betrachtet er die Wellenfunktion explizit nicht im Sinne des wissenschaftlichen Realismus als Abbild oder Modell der Realität, sondern vollzieht einen wörtlich so benannten „Wechsel des erkenntnistheoretischen Standpunkts“. Er charakterisiert die Wellenfunktion als einen „Erwartungskatalog“ aufseiten des Experimentators, der ihm gestattet, das zu erwartende Ergebnis einer jeden Messung mit der größten Genauigkeit vorherzusagen, die die Natur überhaupt erlaubt. In einem Brief an Einstein beschreibt er das Ziel seiner Abhandlung so:

„In einem längeren Aufsatz, den ich eben geschrieben, bringe ich ein Beispiel, das Deinem explodierenden Pulverfaß sehr ähnlich ist. Ich legte bloß Wert darauf, eine Unbestimmtheit ins Spiel zu bringen, die nach heutiger Auffassung wirklich „Heisenbergisch“ und nicht „Boltzmannisch“ ist. In einer Stahlkammer ist ein Geigerzähler ...[es folgt die Beschreibung des Experiments mit der Katze]“

– Erwin Schrödinger

Dementsprechend bleibt Schrödinger dabei, den Zustand des Objekts als eine Wellenfunktion zu betrachten. Das entspricht einem reinen Zustand. Der nach heutiger Auffassung wesentliche Übergang zu einem statistischen Gemisch kommt bei ihm nicht vor.

Kopenhagener Deutung

→ Hauptartikel: Kopenhagener Deutung

Kopenhagener Deutung:
Beim radioaktiven Zerfall erfolgt eine Verzweigung des Zustands. Nach einem Zufallsprinzip kollabiert jedoch einer der beiden Zweige sofort wieder, nachdem die Kohärenz zwischen den Zuständen z. B. aufgrund einer Messung weit genug abgeklungen ist.

In der Kopenhagener Deutung der Quantenmechanik erfolgt im Moment der Messung ein Kollaps der Wellenfunktion des gemessenen Systems. Beim Öffnen des Raums und Beobachtung seines Inneren (Messung) springt der Atomkern, der sich zuvor im Zustand der Überlagerung befand, in einen der zu diesem Messapparat gehörenden Eigenzustände. Erst bei der Messung (hier durch einen äußeren Beobachter) entscheidet sich also, ob die Katze tot oder lebendig ist. Vor der Messung kann über den Zustand der Katze lediglich eine Wahrscheinlichkeitsaussage getroffen werden. Der Messvorgang selbst wird dabei wie in der klassischen Physik beschrieben.

Spätere Interpreten der Kopenhagener Deutung wie Carl Friedrich von Weizsäcker betonen, dass schon das makroskopische Ansprechen der „Höllenmaschine“ die Entstehung eines irreversiblen „Dokuments“ über den erfolgten Atomzerfall zur Folge hat, mit anderen Worten, dass eine Messung stattgefunden hat. Die Wellenfunktion kollabiert ohne weiteres menschliches Zutun; die Katze ist entweder lebendig oder tot.^{[Beleg suchen]}

Mit den 50-Prozent-Wahrscheinlichkeiten für die beiden möglichen Eigenzustände beschreibt die Wellenfunktion vor der Messung gewissermaßen nicht wirklich das System, sondern das unvollständige Wissen über das System. Fröhner hat nachgewiesen, dass die quantenmechanischen Wahrscheinlichkeiten widerspruchsfrei als Bayessche Wahrscheinlichkeiten aufgefasst werden können. Diese ändern sich, indem die Messung den Informationsstand des Beobachters verändert. Dazu wird keine Zeit benötigt; was kollabiert („zusammenbricht“), ist nichts Physikalisches, sondern nur der Informationsmangel des Beobachters. Ganz entsprechend haben sich hierzu Heisenberg 1960 in einer brieflichen Diskussion (siehe Zitat bei Fröhner) und Styer geäußert.

Viele-Welten-Interpretation

→ Hauptartikel: Viele-Welten-Interpretation

Viele-Welten-Interpretation:
Hier verzweigt sich beim Zerfall das gesamte Universum. Gemäß der Theorie bleiben beide Zweige als gleichberechtigte Realitäten erhalten und entwickeln sich von nun an unabhängig voneinander weiter.

Die Viele-Welten-Interpretation ist keine neue oder zusätzliche Theorie, sondern eine alternative Interpretation der Quantenmechanik. Die Viele-Welten-Interpretation spricht allen möglichen Zuständen (also hier „Katze tot“ und „Katze lebendig“) gleichermaßen physikalische Realität zu. Es gibt dann tatsächlich ein Universum, in dem das Atom zerfallen ist, und eines, in dem das Atom noch nicht zerfallen ist, aber die Universen haben keinerlei Kontakt miteinander. In allen Universen gibt es auch uns, ohne dass wir das bemerken könnten. Im ersten Universum öffnen wir den Kasten und finden die Katze tot, im zweiten Universum finden wir die Katze lebendig. Unsere Erinnerungen und das, was wir als „Realität“ wahrnehmen, entsprechen immer nur dem, was in einem von unzähligen möglichen (und gleichermaßen realisierten) Universen stattgefunden hat.

Diese Interpretation wurde 1957 von Hugh Everett veröffentlicht.

Ensembletheorie

Nach der Ensembletheorie kann die Quantenmechanik grundsätzlich keine Einzelsysteme beschreiben, sondern immer nur eine statistische Gesamtheit von Systemen (hier also mehrere, am besten sehr viele Kästen mit Katzen): Nach einem bestimmten Zeitintervall sind dann die Hälfte aller Katzen tot und die andere Hälfte lebendig.

Bohmsche Mechanik

→ Hauptartikel: Bohmsche Mechanik

Bohmsche Mechanik:
Auch diese Theorie berücksichtigt beide Zweige. Jedoch markiert ein deterministischer Mechanismus einen der Zweige als Realität, während alle anderen Zweige als sogenannte Pilotwellen nur die möglichen Quanteninterferenzen auskundschaften.

Die bohmsche Mechanik ist eine alternative Formulierung der Quantenmechanik. Der Zustand eines Teilchens enthält neben der Wellenfunktion zusätzlich eine genaue Ortsangabe, für die eine eigene Bewegungsgleichung aufgestellt wird. Die Beschreibung wird dadurch deterministisch. Jedoch sind diese Orte im Anfangszustand des Systems unbekannt, und daher kann man diesen prinzipiell nicht so genau bestimmen, dass man eine deterministische Voraussage machen könnte. Die Bohmsche Mechanik legt also zu jeder Zeit genau fest, ob die Katze tot oder lebendig ist, kann aber für die Beobachtung nur die Wahrscheinlichkeiten der beiden möglichen Ergebnisse angeben. Diese Form der Quantenmechanik wurde 1952 von David Bohm veröffentlicht.

Katzenzustand

Allgemeines

Angeregt von Schrödingers Katze wird in der Quantenmechanik eine kohärente Überlagerung von zwei Zuständen, die zwei unvereinbar erscheinenden klassischen Zuständen ähnlich sind, als Katzenzustand bezeichnet. Um einen solchen Zustand zu präparieren und wenigstens kurzzeitig zu erhalten, muss möglichst jede Wechselwirkung des Systems mit der Umgebung unterbunden werden. Typische experimentelle Realisierungen beruhten auf Überlagerungen von entgegengesetzten Ausrichtungen von Spins oder von relativ weit entfernten räumlichen Positionen von Teilchen. Erste mesoskopische Katzenzustände einzelner Elektronen wurden mit Elektronenstrahlen erzeugt, die durch Strahlteiler aufgeteilt wurden und bei denen Überlagerungen von Zuständen nachgewiesen wurden, in denen ein Elektron sowohl in dem einen wie auch dem anderen Teilstrahl ist. Mitte der 1990er Jahre ist es gelungen, einen mesoskopischen Katzenzustand für ein einzelnes Atom bezüglich seiner Position zu erzeugen. Darauf aufbauend wurden größere Systeme aus einzelnen Atomen erzeugt. Zum Beispiel wurde mit sechs Atomen die Überlagerung der beiden Zustände hergestellt, bei denen alle Atome den Zustand Spin-Up bzw. alle den Zustand Spin-Down hatten. Auch die kohärente Überlagerung gegenläufiger Kreisströme in einem supraleitenden Ring wurde realisiert.

Katzenzustand beim Quantencomputer

Konkreter Spezialfall ist der Katzenzustand eines Registers in einem Quantencomputer, der auch als Greenberger–Horne–Zeilinger (GHZ) Zustand bezeichnet wird. Er ist die Überlagerung der beiden Zustände, in denen entweder alle Qubits des Registers den Zustand |0⟩ oder alle den Zustand |1⟩ haben. In der Bra-Ket-Notation wird dieser Katzenzustand, als |00…0⟩ +|11…1⟩ geschrieben (mit einem Normierungsfaktor).

Katzenzustand in der Quantenoptik

Wignerfunktion eines quantenoptischen Katzenzustandes mit α=2,5. Neben den beiden Hügeln für $|\alpha \rangle$ und $|{-\alpha }\rangle$ enthält der Katzenzustand eine Interferenzstruktur in der Mitte.

In der Quantenoptik wird eine durch einen komplexen Parameter $\alpha$ bestimmte kohärente Überlagerung der Energie-Eigenzustände $|n\rangle$ eines harmonischen Oszillators als Kohärenter Zustand bezeichnet:

$|\alpha \rangle =e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over {\sqrt {n!}}}|n\rangle$

Die zugehörige Wellenfunktion $\psi _{\alpha }(x)$ hat die Form eines minimalen gaußschen Wellenpakets, das in dem Oszillatorpotential ohne Formänderung harmonisch hin und her schwingt. Der Parameter $\alpha$ bestimmt durch $A={\sqrt {\tfrac {2\hbar }{m\omega }}}\;|\alpha |$ die Schwingungsweite des Mittelpunkts. Der Zustand $|\!-\alpha \rangle$ beschreibt ein Wellenpaket, das genau im Gegentakt schwingt. Als Katzenzustand wird die kohärente Überlagerung

$|\mathrm {cat} _{e}\rangle =N(|\alpha \rangle +|{-}\alpha \rangle )$

bezeichnet, wobei $N$ ein Normierungsfaktor ist. Die Bezeichnung Katzenzustand ergibt sich daraus, dass α und damit die Schwingungsweite prinzipiell beliebig große Werte annehmen kann, und die beiden gegeneinander schwingenden Anteile somit zuweilen räumlich makroskopisch unterscheidbar werden, wie die tote und die lebendige Katze. Die Abbildung zeigt die Wignerfunktion des Katzenzustands mit den beiden Wellenpaketen zu $|\alpha \rangle$ und $|\!-\alpha \rangle$ sowie einem zentralen Maximum, das vom Interferenzterm herrührt.

Bei quantenoptischen Anwendungen ist der Energieeigenzustand $|n\rangle$ ein Fock-Zustand mit $n$ Photonen. Die vergleichsweise einfache Struktur des Zustandes erlaubt systematische theoretische und experimentelle Untersuchungen.

Literatur

• Silvia Arroyo Camejo: Skurrile Quantenwelt, Berlin: Springer, 2006.
• Klaus Mainzer, Jürgen Audretsch [Hrsg.]; Wieviele Leben hat Schrödingers Katze ?, BI Wissenschaftsverlag, Mannheim, 1990, ISBN 3-411-14281-2
• Ernst Peter Fischer: Schrödingers Katze auf dem Mandelbrotbaum: Durch die Hintertür zuer Wissenschaft, Penguin Random House, 2009
• Cord Friebe, Meinard Kuhlmann, Holger Lyre, Paul Näger, Oliver Passon, Manfred Stöckler: Philosophie der Quantenphysik. Einführung und Diskussion der zentralen Begriffe und Problemstellungen der Quantentheorie für Physiker und Philosophen. Springer Spektrum 2015, ISBN 978-3-642-37789-1, Kap. 2.3, 4.2

Weblinks

Wikiquote: Erwin Schrödinger – Zitate

Commons: Schrödingers Katze – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Schrödingers Katze – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Ist Schrödingers Katze tot? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 15. Sep. 2004.
• Schrödingers Katze kann aufatmen – und sei es auch nur ein letztes Mal. quanten.de
• Wie Erwin Schrödingers Katze zu Weltruhm kam. Welt Online, 12. August 2013
• Zvi Schreiber: The nine lives of Schrödingers Cat. Diplomarbeit. Imperial College 1995, Schrödingers Katze in verschiedenen Interpretationen der Quantenmechanik, arxiv:quant-ph/9501014.