Kausalstruktur

In der mathematischen Physik beschreibt die Kausalstruktur einer Lorentzschen Mannigfaltigkeit die kausalen Beziehungen (Relationen) zwischen den Raum-Zeit-Punkten (Ereignissen, englisch events) der Mannigfaltigkeit.

In der modernen Physik (insbesondere der allgemeinen Relativitätstheorie) wird die Raumzeit durch eine Lorentzsche Mannigfaltigkeit dargestellt. Die kausalen Beziehungen zwischen Punkten in dieser Mannigfaltigkeit beschreiben, welche Ereignisse in der Raumzeit welche anderen Ereignisse beeinflussen können.

Die kausale Struktur einer beliebigen (im Allgemeinen nicht ebenen) Lorentzschen Mannigfaltigkeit ist infolge der Krümmung wesentlich kom­pli­zierter als im ebenen Fall, d. h. im Fall eines Minkowski-Raums. Die Diskussion der Kausalstruktur solcher Mannigfaltigkeiten erfolgt über glatte, d. h. differenzierbare, Kurven, die Paare von Raumzeitpunkten (Ereignissen) verbinden. Bedingungen für die Tangentenvektoren der Kurven definieren dann die kausalen Beziehungen.

Tangentenvektoren

Unterteilung der Minkowski-Raumzeit in Be­zug auf einen Punkt in vier disjunkte Mengen. Der Lichtkegel, die kausale Zukunft (Vorwärts-Lichtkegel), die kausale Vergangen­heit (Rückwärts-Lichtkegel) und das (po­ten­ti­ell potentiell gleich­zeitige) „Anderswo“. Die Terminologie wird in diesem Artikel definiert.

Sei $(M,g)$ eine Lorentzsche Mannigfaltigkeit für die Metrik $g$ auf dem Träger $M$ (Menge der Raumzeitpunkte). Als Signatur für die Metrik wird im weiteren Verlauf $(-,+,+,+,\cdots )$ verwendet.

Der Tangentialraum $T_{X}M$ (auch kurz ${\mathcal {T}}_{X}$) an $M$ im (Raum-Zeit-)Punkt (Ereignis) $X$ ist dann ein Minkowski-Vektorraum von Vierervektoren. Da das durch die Metrik $g$ auf diesem Vektorraum induzierte Pseudoskalarprodukt $g_{X}\colon {\mathcal {T}}_{X}\times {\mathcal {T}}_{X}\rightarrow \mathbb {R}$ nicht positiv definit ist, können die Tangenten- oder Vierervektoren $v\in {\mathcal {T}}_{X}$ wie folgt klassifiziert werden:

Nullvektor (englisch zero vector )000	wenn $v=0_{{\mathcal {T}}_{X}}$
lichtartig (englisch null vector )000	wenn $g_{X}(v,v)=0$ und $X\neq 0_{{\mathcal {T}}_{X}}$
zeitartig	wenn $g_{X}(v,v)<0$
raumartig	wenn $g_{X}(v,v)>0$

Anmerkungen:

• Lichtartige Vektoren (mit $g_{X}(v,v)=0$) werden auch als isotrop bezeichnet. Die englische Bezeichnung null vector wird allerdings deutsch oft ebenfalls als Nullvektor (im weiteren Sinn) übersetzt.
• Licht- oder zeitartige Vektoren (mit $g_{X}(v,v)\leq 0$) werden auch als nicht-raumartig oder kausal bezeichnet.

Die kanonische Lorentzsche Mannigfaltigkeit ist die ebene Minkowski-Raumzeit, wobei $M$ ein vierdimensionaler pseudoeuklidischer Raum ist, d. h. $M$≅ $\mathbb {R} ^{4}$ mit der (flachen) Min­kow­ski-Metrik $g$. Die Bezeichnungen für die Klassen der Tangentenvektoren stammen aus der Physik dieses Modells. Die kausalen Be­ziehungen zwischen Punkten sind in der ebenen Minkowski-Raumzeit besonders einfach, weil der Tangentenraum ebenfalls isomorph zum $\mathbb {R} ^{4}$ ist und daher die Raumzeitpunkte nach Festlegung eines Ursprungs mit Tangentenvektoren identifiziert werden können. Der Vierervektor $v$ mit Koordinaten $(t,{\vec {r}})$ wird nach dem Vorzeichen von $g(v,v)=g(v,v)=-c^{2}t^{2}+\|{\vec {r}}\|^{2}$ klassifiziert, wobei ${\vec {r}}\in \mathbb {R} ^{3}$ die kartesischen Koordinaten im dreidimensionalen Raum, $t$ die Zeit und c die universelle Grenzgeschwindigkeit (Vakuumlichtgeschwindigkeit – bei natürlichen Einheiten: $c=1$) ist. Aufgrund der Invarianz der Metrik ist die Klassifizierung jedes Vektors im Raum unabhängig von der Wahl der Bezugssysteme, wenn diese durch eine Lorentz-Transformation miteinander verbunden sind.

Zeitliche Orientierbarkeit

An jedem Punkt (Ereignis) in $M$ können die zeitartigen Tangentenvektoren im Tangentenraum des Punktes in zwei Klassen unterteilt werden. Zu diesem Zweck definiert man zunächst eine Äquivalenzrelation für Paare zeitartiger Tangentenvektoren:

Seien $u$ und $v$ zwei zeitartige Tangentenvektoren an einem Punkt $X$. Man nennt $u$ und $v$ äquivalent (geschrieben $u\sim v$) genau dann, wenn $g(u,v){<}0$.

Es gibt dann zwei Äquivalenzklassen, die unter sich alle zeitartigen Vektoren (und damit Tangentenvektoren am Punkt $E$) aufteilen. Es wird dann eine dieser Äquivalenzklassen willkürlich als zukunftsgerichtet (en. future-directed) und die andere als ver­gangen­heits­gerichtet (en. past-directed) bezeichnen. Physikalisch gesehen entspricht diese Bezeichnung der beiden Klassen von zukunfts- und vergangenheitsgerichteten zeitlichen Vektoren der Wahl eines Zeitpfeils (bei Tangentenvektoren am jeweiligen Punkt $X$). Die Bezeichnungen zukunfts- und vergangenheitsgerichtet können durch stetige Fortsetzung auf lichtartige Vektoren ausgedehnt werden. Beide Äquivalenzklassen zeitartiger Vektoren sind Zu­sam­men­hangs­komponenten, dasselbe gilt für die lichtartigen Vektoren und für die raumartigen Vektoren in Gesamtheit.

Ein Beispiel für einen zukunftsgerichteten Vierervektor ist der Viererimpuls.

Eine Lorentzsche Mannigfaltigkeit ist zeitorientierbar (en. time-orientable), wenn über die gesamte Mannigfaltigkeit eine stetige Bestimmung von zukunftsgerichteten und vergangenheitsgerichteten für nicht-raumartige Vektoren vorgenommen werden kann. Nicht jede Lorentzsche Mannigfaltigkeit ist zeitorientierbar.

Wege und Kurven

Wege bzw. Kurven in der Mannigfaltigkeit werden als zeitartig, raumartig, lichtartig, kausal bezeichnet, wenn die Tangentialvektoren an den Weg bzw. die Kurve auf der gesamten Länge zur entsprechenden Kategorie gehören. Im Detail:

Ein Weg (in der Physik auch Pfad genannt) in $M$ ist eine stetige Abbildung $\mu :\Sigma \to M$, wobei $\Sigma$ ein nicht entartetes Intervall (d. h. eine zusammenhängende Menge von mehr als einem Punkt) in $\mathbb {R}$ ist. Bei einem glatten Weg ist μ eine angemessene Anzahl von Malen ($k$-mal mit $k\geq 1$ bzw. beliebig oft, d. h. $k=\infty$) stetig differenzierbar. Ein regulärer Weg hat eine nicht verschwindende Ableitung.

Eine Kurve in $M$ ist das Bild eines Wegs oder – kategorientheoretisch äquivalent – eine Äquivalenzklasse von Wegen mit gleicher Spur (Bildmenge), die durch Re-Para­metrisierung verwandt sind. Im allgemeinsten Fall müssen diese Parametertransformationen Homöomorphismen (umkehrbar stetig) sein, bei glatten Kurven Diffeomorphismen, bei gerichteten (orientierten) Kurven strikt monoton steigend sein. Für gerichtete Kurven ist sinnvollerweise vorauszusetzen, dass $M$ zeitorientierbar ist.

Glatte reguläre Kurven (oder Wege) in $M$ können anhand ihrer Tangentenvektoren klassifiziert werden. Eine solche Kurve ist

• chronologisch (oder zeitartig), wenn der Tangentenvektor an allen Punkten der Kurve zeitartig ist. Eine solche Kurve wird auch Weltlinie oder Nullgeodäte genannt.
• lichtartig (en. null ) oder Nullkurve, wenn der Tangentenvektor an allen Punkten der Kurve lichtartig (isotrop, en. null vector) ist.
• raumartig, wenn der Tangentenvektor an allen Punkten der Kurve raumartig ist.
• kausal (oder nicht raumartig), wenn der Tangentenvektor an allen Punkten der Kurve zeitartig oder lichtartig ist.

Die Anforderungen der Regularität und Nicht-Entartung der Wege $\Sigma$ stellen sicher, dass geschlossene kausale Kurven (wie solche, die aus einem einzigen Punkt bestehen) nicht automatisch von allen Raumzeiten zugelassen werden (nur von den nicht-zeit­orientier­baren).

Wenn die Mannigfaltigkeit zeitorientierbar ist, können die kausalen (nicht-raumartigen) orientierten Kurven je nach ihrer Orientierung in Bezug auf die Zeit weiter klassifiziert werden. Eine kausale (zeit- oder lichtartige) orientierte Kurve in $M$ ist

• zukunftsgerichtet, wenn für jeden Punkt der Kurve der Tangentenvektor zukunftsgerichtet ist.
• vergangenheitsgerichtet, wenn für jeden Punkt der Kurve der Tangentenvektor vergangenheitsgerichtet ist.

Diese Definitionen gelten nur für kausale (nicht-raumartige) orientierte Kurven, da nur diesen eine Orientierung in Bezug auf die Zeit zugeordnet werden kann.

• Eine geschlossene zeitartige Kurve (geschlossene Weltlinie oder geschlossene Nullgeodäte, en. closed timelike curve, CTC) ist eine geschlossene Kurve, die überall in die Zukunft gerichtet und zeitartig ist, oder überall in die Vergangenheit gerichtet und zeitartig.
• Eine geschlossene Nullkurve ist eine geschlossene Kurve, die überall zukunftsgerichtet und lichtartig ist, oder überall ver­gangen­heits­gerichtet und lichtartig.

Geschlossene Weltlinien gibt es etwa im Gödel-Universum (Kurt Gödel, 1949).

Kausalrelationen

Die Transitivitätsbedingung x≺y,y≺z⇒x≺z wird durch die Kausalitätsbeziehung ≺ in jeder Lorentzschen Raumzeit erfüllt.

Es gibt in der Lorentz-Mannigfaltigkeit $M$ mehrere Arten von kausalen Relationen zwischen Raumzeitpunkten (Ereignissen) $X$ und $Y$:

• $X$ liegt zeitlich vor $Y$ (oft als $X\ll Y$ bezeichnet) genau dann, wenn es eine in die Zukunft gerichtete chronologische (zeitartige) Kurve von $X$ nach $Y$ gibt.
• $X$ geht streng kausal vor $Y$ (oft als $X{<}Y$ bezeichnet) genau dann, wenn es eine in die Zukunft gerichtete kausale (nicht raum­artige) Kurve von $X$ nach $Y$ gibt.
• $X$ geht kausal vor $Y$ (oft als $X\prec Y$ oder $X\leq Y$ bezeichnet) genau dann, wenn $X$ streng kausal vor $Y$ geht oder $X=Y$ ist.
• $X$ horismos $Y$ (oft als $X\to Y$ oder $X\nearrow Y$ bezeichnet), wenn $X=Y$ oder eine zukunftsgerichtete Nullkurve von $X$ nach $Y$ existiert.

Anmerkungen:

• Die kausale Relation $X\prec Y$ alias $X\leq Y$ und die horismos-Relation $X\to Y$ alias $X\nearrow Y$ sind reflexiv.
• Die Mannigfaltigkeit heißt „nicht total bösartig“ (en. non-totally vicious), wenn es (Raumzeit-)Punkte $X\in M$ gibt, für die nicht gilt: $X\ll X$. In Zeichen: $\exists X\in M\colon \neg X\ll X$
• Sie heißt chronologisch, wenn es keine geschlossenen zeitartigen (chronologischen) Kurven gibt, d. h. wenn die chronologische Relation $X\ll Y$ irreflexiv ist, also für alle (Raumzeit-)Punkte $X\in M$ die Relation $X\ll X$ nicht erfüllt ist. In Zeichen: $\forall X\in M\colon \neg X\ll X$
• Sie heißt kausal, wenn es keine geschlossenen kausalen (nicht-raumartigen) Kurven gibt, d. h. wenn für alle (Raumzeit-)Punkte $X,Y\in M$ gilt: Aus $X\prec Y$ und $Y\prec X$ folgt $X=Y$. In Zeichen: $\forall X\in M\colon (X\prec Y\land Y\prec X)\Rightarrow X=Y$.

Im ebenen Fall eines Minkowski-Raumes sind diese Umstände alle trivial und die angegebenen Relationen reflexive oder irreflexive Halbordnungen. Für Lorentz-Mannigfaltigkeiten ist das aber keine Selbstverständlichkeit.

Die Bezeichnung horismos leitet sich ab von altgriechisch ὁρισμός ‚Festlegung‘ und war die Bezeichnung für ein kaiserliches Dekret (Byzantinisches Reich, bekannt seit dem späten 11. Jhd.), es war ein Synonym für Prostagma.

Vergangenheit und Zukunft

Ein gestreckter Zukunfts­licht­kegel

Wenn eine stückweise glatte zeitartige Kurve zwischen zwei Punkten $X,Y\in M$ existiert, liegt ein Punkt in der Zukunft des anderen und dieser in der Vergangenheit des ersteren.

Für einen (Raumzeit-)Punkt $X$ in der Mannigfaltigkeit $M$ definiert man nach Penrose die folgenden Mengen:

• Die chronologische Zukunft (auch zeitartige Zukunft) von $X$, in Zeichen $I^{+}(X)$, ist die Menge aller Punkte $Y$ in $M$, bei denen $X$ chronologisch vor $Y$ ist:

$I^{+}(X)=\{Y\in M|X\ll Y\}$

• Die chronologische Vergangenheit (auch zeitartige Vergangenheit) von $X$, in Zeichen $I^{-}(X)$, als die Menge aller Punkte $Y$ in $M$, bei denen $Y$ chronologisch vor $X$ ist:

$I^{-}(X)=\{Y\in M|Y\ll X\}$

Damit ist $I^{+}(X)$ ist der Inhalt des Zukunfts-Lichtkegels, die Menge aller Punkte $q$, die von $p$ aus mit einer zukunftsgerichteten stückweise glatten zeitartigen Kurve (Weltlinie) erreicht werden können. Analog ist $I^{-}(X)$ der Inhalt des Vergangenheits-Lichtkegels. Der Inhalt des Doppel-Lichtkegels ist damit $I(X):=I^{+}(X)\;\cup$ $I^{-}(X)$. Punkte in $I^{+}(X)$ können von $X$ aus durch eine in die Zukunft gerichtete Weltlinie, die ganz im Innern des Lichtkegels liegt, erreicht werden.

Ähnlich definiert man:

• Die kausale Zukunft (auch absolute Zukunft genannt) von $X$, bezeichnet mit $J^{+}(X)$, ist die Menge aller Punkte $Y$ in $M$, bei denen $X$ kausal vorausgeht vor $Y$:

$J^{+}(X)=\{Y\in M|X\prec Y\}$

• Die kausale Vergangenheit (auch absolute Vergangenheit genannt) von $X$, bezeichnet als $J^{-}(X)$, ist die Menge aller Punkte $Y$ in $M$, bei denen $Y$ kausal vorausgeht vor $X$:

$J^{-}(X)=\{Y\in M|Y\prec X\}$

Die kausale Zukunft $J^{+}(X)$ ist daher die Menge aller Punkte, die mit stückweise glatten nicht-raumartigen Kurven erreicht werden. Entsprechend definiert kausale Vergangenheit $J^{-}(X)$. Der Punkt $X$ kann umgekehrt von den Punkten in $J^{-}(X)$ aus durch eine in die Zukunft gerichtete nicht-raumartige Kurve erreicht werden. Die Synonymie von „nicht-raumartig“ und „kausal“ rührt von der Annahme her, dass sich Ursache und Wirkung mit maximal Lichtgeschwindigkeit ausbreiten können, d. h. teilweise (abschnittsweise) mit Lichtgeschwindigkeit („lichtartig“ wie das Licht) und teilweise darunter („zeitartig“ wie Materie – mehr Zeit als Raum verbrauchend). Diese Mengen entsprechen geometrisch einem (ggf. verzerrten) Vollkegel (Kegelkörper), einschließlich des Kegelmantels als Rand-Hyperfläche. Der Doppel-Vollkegel ist damit $J(X):=J^{+}(X)\;\cup$ $J^{-}(X)$.

• Der Zukunfts-Nullkegel (Vorwärts-Lichtkegel) von $X$ ist die Menge aller Punkte $Y$ in $M$, für die gilt: $X\to Y$.
• Der Vergangenheits-Nullkegel (Rückwärts-Lichtkegel) von $X$ ist die Menge aller Punkte $Y$ in $M$, für die gilt: $Y\to X$
• Der Nullkegel (Lichtkegel) von $X$ wird definiert als die Vereinigung von Zukunfts- und Vergangenheits-Nullkegel (Vorwärts- und Rückwärts-Lichtkegel) von $X$.

• Das Anderswo (en. elsewhere) von $X$ ist die Menge aller Punkte, die nicht im Lichtkegel, in der kausalen Zukunft oder in der kausalen Vergangenheit liegen.

Für den Fall, dass die so definierten Relationen die Bedingungen für Halbordnungen erfüllen, handelt es sich bei den Lichtkegeln um Ordnungskegel. Notwendige Voraussetzung dafür ist, dass es keine geschlossenen Weltlinien gibt.

In der flachen Minkowski-Raumzeit ist diese Bedingung erfüllt und es liegen Halbordnungsrelationen bzw. Ordnungskegel vor. Ein Lichtkegel ist hier eine Menge von Raumzeitpunkten, die zu $X$ vermittels eines zeitartigen (Parallel­ver­schiebungs-)Vektors zu erreichen sind, also das vierdimensionale Innere eines idealen vierdimensionalen Kegels, im dreidimensionalen einem geraden Kreiskegel entsprechend, nur dass hier die Kegelschnitte Kugeln sind (da sich ein von einem Punkt ausgehender Lichtblitz kugelförmig ausbreitet). Die vermöge eines lichtartigen Vektors erreichbaren Punkte bilden den Kegelmantel (Rand des Kegels), eine dreidimensionale Hyperfläche (vgl. Differenzierung zwischen Kugelfläche und Kugelkörper), die oben als Zukunfts-Nullkegel eingeführt wurde.

Kausalstruktur (Definition)

Die Zuordnungen $X\mapsto I^{+}(X),I^{-}(X),J^{+}(X),J^{-}(X)$, die für alle $X$ in $M$ definiert sind, werden zusammen als die kausale Struktur (oder Kausalstruktur) von $(M,g)$ bezeichnet.

Anmerkung:
Dieser Sprachgebrauch weicht etwas ab von dem in der Mathematik relationaler Strukturen üblichen, bei der eine Träger­menge – wie $M$ – oder Trägerstruktur – wie $(M,g)$ mit den zugehörigen Relationen zu einem Tupel zusammengefasst wird. Das wäre hier etwa $(M,\ll ,\leq )$ oder ausführlicher $(M,g,\ll ,{<},\nearrow )$. Da aber stets folgende logische Äquivalenzen gelten:

$Y\in I^{+}(X)\Leftrightarrow X\ll Y$

$Y\in I^{-}(X)\Leftrightarrow Y\ll X$

$Y\in J^{+}(X)\Leftrightarrow X\prec Y$

$Y\in J^{-}(X)\Leftrightarrow Y\prec X$

so können die Relationen aus den Ordnungskegeln zurückgewonnen werden, weshalb diese Definitionen (kategorientheoretisch) äquivalent sind und dieselbe Struktur beschreiben.

Weitere Begriffsdefinitionen

Für eine Teilmenge $S$ von $M$ definiert man als mengentheoretischen Vereinigungen:

$I^{\pm }[S]:=\bigcup _{X\in S}I^{\pm }(X)\equiv \bigcup \{I^{\pm }(X)|X\in S\}$

$J^{\pm }[S]:=\bigcup _{X\in S}J^{\pm }(X)\equiv \bigcup \{J^{\pm }(X)|X\in S\}$

Für zwei Teilmengen $S,T$ von $M$ definiert man:

• Die chronologische Zukunft von $S$ in Bezug auf $T$, $I^{+}[S;T]$, ist die chronologische Zukunft von $S$ als Untermannigfaltigkeit von $T$. Man beachte, dass dies ein ganz anderes Konzept ist als die Schnittmenge $I^{+}[S]\cap T$, das die Menge der Punkte in $T$ angibt, die vermöge von $S$ ausgehender zukunftsgerichteter zeitartiger Kurven erreicht werden können. Im ersten Fall (der Definition hier) müs­sen die Kurven nämlich ganz in $T$ liegen, im anderen Fall nicht. Siehe Hawking und Ellis (1973).
• Die chronologische Vergangenheit von $S$ in Bezug auf $T$, $I^{-}[S;T]$, wird analog definiert.
• Die kausale Zukunft von $S$ relativ zu $T$, $J^{+}[S;T]$, ist die kausale Zukunft von $S$, betrachtet als Untermannigfaltigkeit von $T$. Man beachte, dass dies wieder ein ganz anderes Konzept ist als die Schnittmenge $J^{+}[S]\cap T$, das die Menge der Punkte in $T$ angibt, die vermöge von $S$ ausgehender zukunftsgerichteter Kausalkurven erreicht werden können. Im ersten Fall (der Definition hier) müssen die Kurven komplett in $T$ liegen, im anderen Fall nicht. Siehe ebenfalls Hawking und Ellis (1973).
• Die kausale Vergangenheit von $S$ relativ zu $T$, $J^{+}[S;T]$, wird wieder analog definiert.

• Eine Zukunftsmenge (en. future set) ist eine unter chronologischer Zukunft abgeschlossene Menge.
• Eine Vergangenheitsmenge (en. past set) ist eine unter chronologischer Vergangenheit abgeschlossene Menge.
• Eine unzerlegbare Vergangenheitsmenge (en. indecomposable past set, IP) ist eine Vergangenheitsmenge, die nicht die Ver­ei­ni­gung von zwei verschiedenen offenen Vergangenheitsmengen ist.
• Eine IP, die nicht mit der Vergangenheit eines beliebigen Punktes $X$ in $M$ zusammenfällt, nennt man eine terminale unzerlegbare Vergangenheitsmenge (terminal indecomposable past set TIP).
• Eine eigentliche unzerlegbare Vergangenheitsmenge (proper indecomposable past set, PIP) ist eine IP, die keine TIP ist. $I^{-}(X)$ ist eine eigentliche unzerlegbare Vergangenheitsmenge (PIP).

• Sei $S$ eine Teilmenge von $M$. Die Zukunfts-Cauchy-Entwicklung oder zukünftiger Domäne der Abhängigkeit (en. future Cauchy development bzw. future domain of dependence) von $S$, bezeichnet mit $D^{+}(S)$ (oder auch $D_{+}(S)$), ist die Menge aller Punkte $X$, für die jede vergangenheitsgerichtete, nicht erweiterbare Kausalkurve durch $X$ die Menge $S$ mindestens einmal (im mengentheoretischen Sinn) schneidet. Formal:

$D^{+}(S)\equiv D_{+}(S):=\{p\in M|$jede vergangenheits­nicht­erweiterbare kausale Kurve durch $p$ trifft $S\}$, englisch:

$D^{+}(S):=\{p\in M|$every past inextendible causal curve through $p$ intersects $S\}$

• Dieselbe umgangssprachliche Bezeichnung wird benutzt für ${\tilde {D}}^{+}(S)$ (alias ${\tilde {D}}_{+}(S)$), der Menge aller Punkte $X$, für die jede ver­gangen­heits­ge­richtete, nicht erweiterbare zeitartige Kurve durch $X$ die Menge $S$ mindestens einmal (im mengentheoretischen Sinn) schneidet. Formal:

${\tilde {D}}^{+}(S)\equiv D_{+}(S):=\{p\in M|$jede vergangenheits­nicht­erweiterbare zeitartige Kurve durch $p$ trifft $S\}$, englisch:

${\tilde {D}}^{+}(S):=\{p\in M|$every past inextendible timelike curve through $p$ intersects $S\}$

• Analog wird die Vergangenheits-Cauchy-Entwicklung (en. past Cauchy development) definiert, in Zeichen $D^{-}(S)$ (oder auch $D_{-}(S)$) bzw. ${\tilde {D}}^{-}(S)$ (oder auch ${\tilde {D}}_{-}(S)$).
• Die Cauchy-Entwicklung (schlechthin) ist die Vereinigung der zukünftigen und vergangenen Cauchy-Entwicklungen. In Zeichen:

$D(S):=D^{+}(S)\cup D^{-}(S)$, und analog wäre dann $D(S):=D^{+}(S)\cup D^{-}(S)$.

Cauchy-Entwicklungen sind wichtig für die Untersuchung des Determinismus. Es gilt $D^{+}(S)\subset$ ${\tilde {D}}^{+}(S)$.

• Eine Teilmenge $S\subset M$ heißt achronal genau dann, wenn es keine Ereignisse $q,r\in S$ gibt, so dass $r\in I^{+}(q)$ gilt; oder gleich­wertig, wenn $S$ disjunkt von $I^{+}[S]$ ist.
• Eine Cauchy-Oberfläche ist eine geschlossene achronale Menge, deren Cauchy-Entwicklung ganz $M$ umfasst.

Diamant-Menge und Kau­sal­dia­mant

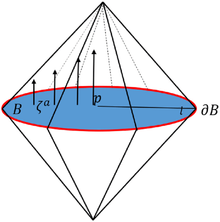
• Eine Metrik ist global hyperbolisch, wenn sie sich als Blätterung von Cauchy-Flächen darstellen lässt (en. if it can be foliated by Cauchy surfaces).

• Eine chronologieverletzende Menge ist eine Menge von (Raumzeit-)Punkten, durch die (mindestens) eine geschlossene zeitartige Kurven verläuft.
• Eine kausalitätsverletzende Menge ist eine Menge von Punkten, durch die eine geschlossene Kausalkurve verläuft.
• Für zwei (Raumzeit-)Punkte $X,Y\in M$ ist die Diamant-Menge (auch Alexandrow-Intervall, en. Alexandrov interval genannt) gegeben durch $A(X,Z):=I^{+}(X)\cap I^{-}(Z)=\{Y\in M|X\ll Y\ll Z\}$
• Für eine Kausalkurve $\gamma$ ist der Kausaldiamant (en. causal diamond ) $J^{+}[\gamma ]\cap J^{-}[\gamma ]\;$. Das bedeutet: Der Kausaldiamant der Weltlinie $\gamma$ eines Teilchens ist die Menge aller Ereignisse, die sowohl in der Vergangenheit eines Punktes in $\gamma$ als auch in der Zukunft eines Punktes in $\gamma$ liegen.

Zur Thermodynamik der Kausaldiamanten siehe beispielsweise Jakobson & Visser (2019).

Eigenschaften

• Der Rand einer kausalitätsverletzenden Menge ist ein Cauchy-Horizont.
• Weitere Eigenschaften nach Penrose (1972):
  Für alle (Raumzeit-)Punkte $X\in M$ gilt:
  • $X$ ist in $I^{-}(Y)$ dann und nur dann, wenn $Y$ in $I^{+}(X)$ ist; formal:
    $X\in I^{-}(Y)\Leftrightarrow Y\in I^{+}(X)$
  • $X\prec Y\implies I^{-}(X)\subset I^{-}(Y)$
  • $X\prec Y\implies I^{+}(Y)\subset I^{+}(X)$

Für jede Teilmenge $S\subset M$ gilt:

• $I^{+}[S]=I^{+}[I^{+}[S]]\subset J^{+}[S]=J^{+}[J^{+}[S]]$
• $I^{-}[S]=I^{-}[I^{-}[S]]\subset J^{-}[S]=J^{-}[J^{-}[S]]$

• Topologische Eigenchaften:
  • $I^{\pm }(x)$ ist offen für alle (Raumzeit-)Punkte $x\in M$.
  • $I^{\pm }[S]$ ist offen für alle Teilmengen $S\subset M$.
  • $I^{\pm }[S]=I^{\pm }[{\overline {S}}]$ für alle Teilmengen $S\subset M$.
  • $I^{\pm }[S]\subset {\overline {J^{\pm }[S]}}$

Dabei bezeichnet ${\overline {S}}$ die abgeschlossene Hülle einer Teilmenge $S\subset M$.

Zum Thema starke und schwache kosmische Zensur siehe z. B. Flores (2007)

Konforme Geometrie

→ Hauptartikel: Konforme Abbildung §Konforme Abbildungen auf (semi-)riemannschen Mannigfaltigkeiten

Seien gegeben $(M,g)$ und $(M,{\hat {g}})$ als zwei Riemannsche Mannigfaltigkeiten (Spezialfall: Lorenztsche Mannigfaltigkeiten) mit derselben Trägermenge (Raumzeit) $M$, aber im Allgemeinen verschiedenen Metriken $g$ und ${\hat {g}}$.

$g$ und ${\hat {g}}$ heißen konform äquivalent (en. conformally related oder conformally equivalent) genau dann, wenn es eine auf $M$ definierte glatte (hinreichend oft differenzierbare) positive Abbildung $u:M\to \mathbb {R} ^{+}\;\;$ gibt derart, dass gilt:

$g=u\cdot {\hat {g}}$,

soll heißen:
Für jedes $X\in M$ seien die auf dem Tangentialraum ${\mathcal {T}}_{X}=T_{X}M$ gegebenen Metriken mit $g_{x}$ und ${\hat {g}}_{x}$ bezeichnet. Dann gilt:

$g_{x}=u(x)\cdot {\hat {g}}_{x}$

Eine Abbildung $u$ dieser Art wird konformer Faktor (oder konforme Skalierung) genannt.

Äquivalente Formulierungen verlangen eine glatte (nicht immer als positiv vorausgesetzte) Funktion $\Omega :M\to \mathbb {R}$ und

$g=\Omega ^{2}\cdot {\hat {g}}$ bzw. $g_{x}=\Omega (x)^{2}\cdot {\hat {g}}_{x}$

und bezeichnen die Abbildung $\Omega$ als konformen Faktor. Von dieser Konvention abgesehen sind beide Definitionen gleichwertig und gehen mit $u=\Omega ^{2}$ ineinander über.

• Die Klasse untereinander konform äquivalenter Metriken auf $M$ heißt konforme Struktur.
• Die obige Definition kann in geeigneter Weise auf Riemannsche Mannigfaltigkeiten $(M,g)$ und $({\hat {M}},{\hat {g}})$ erweitert werden, siehe Konforme Abbildung.

Betrachtet man die Definitionen, welche Tangentenvektoren zeitarig, lichtartig oder raumartig sind, so sieht man, dass sie unverändert bleiben, wenn man eine Metrik $g$ oder eine konform äquivalente Metrik ${\hat {g}}$ zugrunde legt.

Nimmt man als Beispiel an, dass im Raumzeit-Punkt $X$ $v\in {\mathcal {T}}_{X}$ ein zeitartiger Tangentialvektor in Bezug auf die $g_{X}$-Metrik sei. Das bedeutet $g_{X}(v,v)<0$. Es ist dann ${\hat {g}}_{X}(v,v)=\Omega ^{2}g_{X}(v,v)<0$, also ist $v$ auch ein zeitartiger Tangentenvektor bezüglich der Metrik ${\hat {g}}_{X}$.

Daraus folgt, dass die kausale Struktur einer Lorentzschen Mannigfaltigkeit durch eine konforme Transformation unberührt bleibt. Insbesondere bleibt eine Null-Geodäte unter einer konformen Skalierung eine Null-Geodäte.

Theorem von Malament

Das Theorem von Malament (genauer: Malament, Hawking-McCarthy-King, Levichev), das folgendes besagt:
Wenn es eine bijektive Abbildung $f\colon M_{1}\to M_{2}$ zwischen zwei Raumzeiten $(M_{1},g_{1})$ und $(M_{1},g_{1})$ mit Dimension > 2 gibt, die bzgl. der Kausalstruktur treu ist (sie erhält), d. h. für die gilt:

$X\ll Y\Leftrightarrow f(X)\ll f(Y)$ für alle $X,Y\in M$ (oder analog mit ${<}$ statt$\ll$),

dann sind $(M_{1},g_{1})$ und $(M_{2},g_{2})$ konform isometrisch und $f$ ein konformer Isomorphismus.

Der konforme Faktor bleibt dabei zunächst unbestimmt. Er hängt mit dem Volumen der Regionen in der Raumzeit zusammen. Dieser Volumenfaktor lässt sich ermitteln, indem für jeden Raumzeitpunkt ein Volumenelement angegeben wird. Das Volumen einer Raumzeitregion könnte dann durch Zählen der Anzahl der Punkte in dieser Region ermittelt werden, wenn eine lokal diskrete Kausalmenge zugrunde gelegt wird.

Penrose-Diagramm

→ Hauptartikel: Penrose-Diagramm

Eine unendliche Metrik lässt Geodäten von unendlicher Länge und echter Zeit (en. infinite length/proper time) zu. Manchmal kann man jedoch eine konforme Neuskalierung der Metrik mit einem konformen Faktor vornehmen, der bei Annäherung an das Unendliche ausreichend schnell auf 0 abfällt, um so einen konformen Rand (en. conformal boundary) der Mannigfaltigkeit zu erhalten. Die topologische Struktur des konformen Randes hängt von der kausalen Struktur ab.

• Zukunftsgerichtete zeitartige Geodäten enden in $i^{+}$, der zukünftigen zeitartigen Unendlichkeit.
• Vergangenheitsgerichtete zeitartige Geodäten enden in $i^{-}$, der vergangenen zeitartigen Unendlichkeit.
• Zukunftsgerichtete Null-Geodäten enden in ℐ$^{+}$, der zukünftigen Nullunendlichkeit.
• Vergangenheitsgerichtete Null-Geodäten enden in ℐ$^{-}$, der vergangenen Nullunendlichkeit.
• Raumartige Geodäten enden auf der raumartigen Unendlichkeit.
• Für den ebenen Minkowski-Raum sind $i^{\pm }$ Punkte, ℐ$^{\pm }$ sind Nullblätter (en. null sheets), und die raumartige Unendlichkeit hat die Kodimension 2.
• Für den Anti-de-Sitter-Raum gibt es keine zeitartige oder Null-Unendlichkeit, und die raumartige Unendlichkeit hat die Kodimension 1.
• Für den de-Sitter-Raum hat dagegen die zukünftige und vergangene zeitartige Unendlichkeit die Kodimension 1.

Siehe auch Penrose-Diagramm und Holografisches Prinzip.

Siehe auch

• Gerichtete Menge
• Kausalmenge
• Penrose-Diagramm
• Singularitäten-Theorem
• Raumzeit

Weiterführende Literatur

• Gary W. Gibbons, Sergey N. Solodukhin: The Geometry of Small Causal Diamonds. Auf: arXiv, DAMTP-2007-22, Corpus ID: 6877849, 9. März 2007; arXiv:hep-th/0703098, doi:10.1016/j.physletb.2007.03.068, Epub 12. August 2015. (Kausal-Intervale und -Diamanten)
• Jinzhao Wang: Geometry of small causal diamonds. Auf: Phys. Rev. D, Band 100, 11. September 2019, S. 064020; doi:10.1103/PhysRevD.100.064020. (Kausal-Diamanten)
• Stephen W. Hawking, Andrew R. King, P. J. McCarthy: A new topology for curved space–time which incorporates the causal, differential, and conformal structures. In: J. Math. Phys., Band 17, Nr. 2, 1976, S. 174–181. (Geometrie, Kausalstruktur)
• Alexander V. Levichev: Prescribing the conformal geometry of a lorentz manifold by means of its causal structure. In: Soviet Math. Dokl., Band 35, 1987, S. 452–455. (Geometrie, Kausalstruktur)
• David B. Malament: The class of continuous timelike curves determines the topology of spacetime. In: J. Math. Phys., Band 18, Nr. 7, 1977, S. 1399–1404; doi:10.1063/1.523436. (Geometrie, Kausalstrukture)
• Alfred A. Robb: A theory of time and space. Cambridge University Press, 1914. (Geometrie, Kausalstruktur)
• Alfred A. Robb: The absolute relations of time and space. Cambridge University Press, 1921. (Geometrie, Kausalstruktur)
• Alfred A. Robb: Geometry of Time and Space. Cambridge University Press, 1936. (Geometrie, Kausalstruktur)
• Rafael D. Sorkin, Eric Woolgar: A Causal Order for Spacetimes with C⁰ Lorentzian Metrics: Proof of Compactness of the Space of Causal Curves. In: Classical & Quantum Gravity 1971–1994, Band 13, 1996. arXiv:gr-qc/9508018 (Kausalstruktur)
• Benjamin F. Dribus: Entropic Phase Maps in Discrete Quantum Gravity. In: MDPI Entrpy, Band 19, Nr. 7, 30. June 2017, S. 322, Special Issue Quantum Information and Foundations; doi:10.3390/e19070322. (Entropie, Gerichtete Mengen)

Weblinks

• Enrique Zeleny: Turing Machine Causal Networks. Auf: Wolfram Demonstrations Project (wolfram.com)
• Eric W. Weisstein: CausalNetwork. Auf: MathWorld (wolfram.com)

Nachweise

• Stephen W. Hawking, George Francis Rayner Ellis: The Large Scale Structure of Space-Time. Cambridge University Press, 10. Mai 1973, ISBN 0-521-20016-4, doi:10.1017/CBO9780511524646, Epub Januar 2010
• Stephen W. Hawking, Werner Israel: General Relativity: an Einstein Centenary Survey. Cambridge University Press, 1979
• Roger Penrose: Techniques of Differential Topology in Relativity. Society for Industrial and Applied Mathematics (SIAM): CBMS-NSF Regional Conference Series in Applied Mathematics, 1972; ISBN 0-89871-005-7, doi:10.1137/1.9781611970609.
• Robert D. Sard: Relativistic Mechanics - Special Relativity and Classical Particle Dynamics, in: Lecture notes and supplements in physics, Ausgabe 13, W. A. Benjamin Inc., New York, 1. Januar 1970, 376 Seiten, Google Books, Epub 6. Februar 2010; Paperback, Addison-Wesley Longman Inc., ISBN 978-0-8053-8491-8, 376 Seiten, Juli 1970.