Magisches Dürer-Quadrat

Detail aus Melencolia I

Das magische Dürer-Quadrat zählt zu den berühmtesten magischen Quadraten und ist in Albrecht Dürers Kupferstich Melencolia I abgebildet.

Eigenschaften von Summenkombinationen

Das Dürer-Quadrat ist ein symmetrisches magisches Quadrat und besitzt 86 Summenkombinationen der magischen Zahl 34.

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

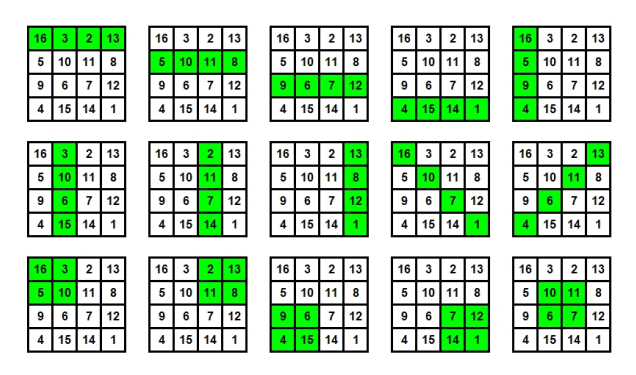
Zur besseren Übersicht sind nachfolgend alle Summenkombinationen nach verschiedenen Eigenschaften gruppiert, wobei möglicherweise auch andere Gruppierungen denkbar sind. Als Orientierung dient jeweils ein Bild, in dem die betreffenden Summenkombinationen mit grüner Hintergrundfarbe gekennzeichnet sind.

• 
  Abbildung 1
• 
  Abbildung 2
• 
  Abbildung 3
• 
  Abbildung 4
• 
  Abbildung 5
• 
  Abbildung 6

Zu Abbildung 1: 15 Summenkombinationen:

Die waagerechten, senkrechten und diagonalen Reihen sowie die zweireihigen Eckquadrate und das zweireihige Mittelquadrat haben jeweils die Summe 34.

Zu Abbildung 2: 21 Summenkombinationen:

Die Eckzahlen des Dürer-Quadrats sowie die Eckzahlen von Rechtecken und dreihreihigen Quadraten, die an den Rändern angrenzen, haben jeweils die Summe 34. Dies gilt auch für die diagonal einbeschriebenen Rechtecke sowie für die Eckzahlen zweier Lateinischer Kreuze und zweier Petruskreuze, die auch als Eckzahlen von Drachenvierecken aufgefasst werden können.

Zu Abbildung 3: 12 Summenkombinationen:

Die am Zentrum gespiegelten waagerechten und senkrechten benachbarten Zahlenpaare sowie die am Zentrum gespiegelten Rösselsprünge haben jeweils die Summe 34.

Zu Abbildung 4: 8 Summenkombinationen:

Die Zahlen der beiden mittleren Zeilen und Spalten in Zickzack-Reihenfolge und die Zahlen an den äußeren Zeilen und Spalten in Zickzack-Reihenfolge haben jeweils die Summe 34.

Zu Abbildung 5: 12 Summenkombinationen:

Gewisse L-förmige und T-förmige Muster haben jeweils die Summe 34.

Zu Abbildung 6: 18 Summenkombinationen:

Sonstige Muster mit nicht-symmetrischen Kombinationen, die jeweils die Summe 34 haben.

Zusätzlich besitzt das Dürer-Quadrat die Eigenschaft, dass jedes zum Mittelpunkt punktsymmetrische Zahlenpaar die Summe 17 hat.

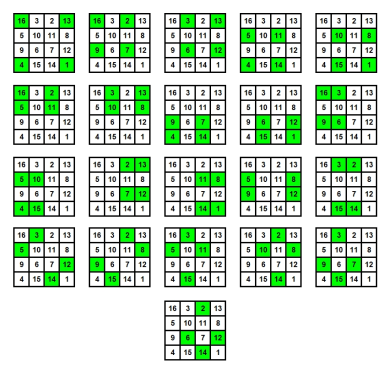
Eigenschaften von Quadrat- und Kubiksummensummenkombinationen

Die Quadratzahlen der acht Zahlen in den Feldern der folgenden Achterkombinationen haben jeweils die Summe 748:

• Diagonalenpaar,
• Paare in der Mitte der Ränder,
• erste und dritte Zeile,
• zweite und vierte Zeile,
• erste und dritte Spalte,
• zweite und vierte Spalte.

Die Kubikzahlen der acht Zahlen in den Feldern der folgenden Achterkombinationen haben jeweils die Summe 9248:

• Diagonalenpaar,
• Paare in der Mitte der Ränder.

Alle sechs Achterkombinationen bilden offensichtlich symmetrische Muster.

• Das Diagonalenpaar sowie die die Gesamtheit der Paare in der Mitte der Ränder sind jeweils symmetrisch zur waagerechten und senkrechten Mittelachse sowie zu den beiden Diagonalen.
• Die Kombination aus der ersten und dritten Zeile sowie die aus der zweiten und vierten Zeile sind jeweils symmetrisch zur senkrechten Mittelachse.
• Die Kombination aus der ersten und dritten Spalte sowie die aus der zweiten und vierten Spalte sind jeweils symmetrisch zur waagerechten Mittelachse.

In der folgenden Abbildung sind die Quadratsummeneigenschaften grün und gelb und die Kubiksummeneigenschaften grün dargestellt.

Literatur

• Wolfgang Göbels: Varianten des magischen Quadrats von Albrecht Dürer. In: Praxis der Mathematik. (PM) Band 4, Nr. 35, Jahrgang 1993, Aulis Verlag.
• Christoph Pöppe: Edle magische Quadrate. In: Spektrum der Wissenschaft. Januar 1996, S. 14 ff

Weblinks

Commons: Melencolia magic square – Sammlung von Bildern, Videos und Audiodateien

• Magic square in der Encyclopaedia of Mathematics
• Eric W. Weisstein: Magic Square. In: MathWorld (englisch).
• Magische Quadrate – umfangreiche Website mit Buch als PDF
• Magische Quadrate auf w.hp-gramatke.de (umfangreiches Material zu magischen Quadraten)
• Seite des Künstlers Paul Heimbach, Köln
• Betrachtung Magischer Quadrate mit Ausführungen über die Summenkombinationen im Magischen Quadrat von Albrecht Duerer auf mathematische-basteleien.de
• Jürgen Kühl: Ein besonderes Magisches Quadrat Internetarchiv WaybackMachine, abgerufen am 10. September 2022