Maxwell-Bloch-Gleichungen

Die Maxwell-Bloch-Gleichungen beschreiben die Wechselwirkung eines Ensembles quantenmechanischer Zweiniveausysteme mit einem oszillierenden elektrischen Feld. Sie werden zur Beschreibung von Absorption und Emission von Licht in Festkörpern und Gasen verwendet und spielen insbesondere beim theoretischen Verständnis der Verstärkung in Lasern eine zentrale Rolle. Voraussetzung ist dabei, dass die Energiedifferenz des Übergangs nahe bei der Photonenenergie des Lichts ist und, dass die anderen Übergänge des Systems deutlich andere Übergangsenergien besitzen.

Gleichungen

Die Maxwell-Bloch-Gleichungen lauten

$\partial _{t}{\mathcal {P}}=\left[i(\omega -\Omega )-{\frac {1}{\tau _{p}}}\right]{\mathcal {P}}+{\frac {|d_{12}|^{2}}{i\hbar }}\Delta n{\mathcal {E}}\quad ~$ $\partial _{t}\Delta n={\frac {1}{\hbar }}{\text{Im}}\left({{\mathcal {E}}^{*}{\mathcal {P}}}\right)-{\frac {n_{0}+\Delta n}{\tau }}$ $\left(\partial _{z}+{\frac {1}{c_{g}}}\partial _{t}\ \right){\vec {\mathcal {E}}}={\frac {i}{2}}\mu _{0}\omega c_{p}{\vec {\mathcal {P}}}$

mit:

• ${\vec {\mathcal {E}}}$: komplexe Amplitude des elektrischen Felds
• ${\vec {\mathcal {P}}}$: komplexe Amplitude der Polarisation
• $\Delta n=n_{2}-n_{1}$: Besetzungsinversion mit $n_{2}$ und $n_{1}$ Besetzungszahldichte der Niveaus 1 und 2
• $n_{0}=n_{1}+n_{2}$: Zahl der Zweiniveausysteme pro Volumen
• $\omega$: Frequenz des elektrischen Feldes
• $\Omega$: Frequenz des Übergangs mit $\Omega ={\frac {E_{2}-E_{1}}{\hbar }}$
• $\tau _{p}$: Phasenrelaxationszeit, Kohärenzzeit der Polarisation.
• $\tau$: Lebensdauer des zweiten Zustandes
• $d_{12}=e\left\langle \varphi _{1}\right|{\vec {r}}\cdot {\vec {e_{E}}}\left|\varphi _{2}\right\rangle$ Projektion des Dipolübergangsmatrixelement auf die Richtung des elektrischen Feldes
• $c_{g}=\partial _{k}\omega$: Gruppengeschwindigkeit im Medium
• $\mu _{0}$: Magnetische Feldkonstante
• $c_{p}={\frac {\omega }{k}}={\frac {c_{0}}{n}}$: Phasengeschwindigkeit im Medium

Näherungen

Kohärentes Regime

Im kohärenten Regime nimmt man an, dass die typischen Zeitableitungen von $\Delta n$ und ${\mathcal {P}}$ sehr viel größer als die Zerfallsterme sind, also

$\left|\partial _{t}{\mathcal {P}}\right|\gg \left|{\frac {\mathcal {P}}{\tau _{p}}}\right|\quad {\text{und}}\quad \left|\partial _{t}\Delta n\right|\gg \left|{\frac {\Delta n}{\tau _{p}}}\right|$

gilt. Damit nehmen die Maxwell-Bloch-Gleichungen die Form

$\partial _{t}{\mathcal {P}}=\left[i(\omega -\Omega )\right]{\mathcal {P}}+{\frac {|d_{12}|^{2}}{i\hbar }}\Delta n{\mathcal {E}}$

$\partial _{t}\Delta n={\frac {1}{\hbar }}{\text{Im}}\left({{\mathcal {E}}^{*}{\mathcal {P}}}\right)$

$\left(\partial _{z}+{\frac {1}{c_{g}}}\partial _{t}\ \right){\vec {\mathcal {E}}}={\frac {i}{2}}\mu _{0}\omega c_{p}{\vec {\mathcal {P}}}$

an. Man kann leicht zeigen, dass in diesem Fall

$\left|{\mathcal {P}}\right|^{2}+\left|d_{12}\right|^{2}\Delta n^{2}={\text{const}}=\left|d_{12}\right|^{2}n_{0}^{2}$

gilt. Deshalb liegt die Einführung des sog. Bloch-Vektors

${\vec {\mu }}={\frac {1}{|d_{12}|n_{0}}}{\begin{pmatrix}{\text{Re}}({\mathcal {P}})\\-{\text{Im}}({\mathcal {P}})\\\Delta n|d_{12}|\\\end{pmatrix}}$

mit $|\mu |^{2}=1$ nahe. Für diesen gilt die Bewegungsgleichung

${\dot {\vec {\mu }}}={\vec {\mu }}\times {\vec {R}}\quad {\text{mit}}\quad {\vec {R}}={\begin{pmatrix}{\text{Re}}(\Omega _{R})\\-{\text{Im}}(\Omega _{R})\\-\Delta \\\end{pmatrix}}$

mit der sog. Rabi-Frequenz $\Omega _{R}(t)={\frac {|d_{12}|{\mathcal {E}}(t)}{\hbar }}$ und der Verstimmung $\Delta =\omega -\Omega$.

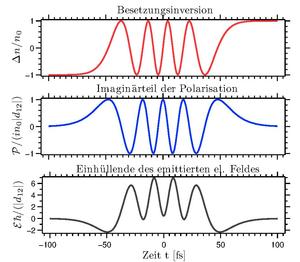
Lösung der Maxwell-Bloch-Gleichungen im kohärenten Regime mit resonanter Kopplung für einen gaussförmigen $\pi$-Puls ($\Theta (\infty )=9\pi$). Hierbei sind sog. Rabioszillationen zu sehen.

Im Fall der sog. resonanten Kopplung, d. h. $\omega =\Omega \Rightarrow \Delta =0$ und ${\mathcal {E}}$ reell findet man die Gleichungen

$\partial _{t}{\mathcal {P}}=in_{0}\Omega _{R}|d_{12}|\Delta n$

$\partial _{t}\Delta n=-n_{0}\Omega _{R}|d_{12}|{\mathcal {P}}.$

Die Lösungen dieses Differentialgleichungssystems lauten

${\mathcal {P}}=in_{0}|d_{12}|\sin(\Theta (t))$ $\Delta n=-n_{0}\cos(\Theta (t))$

mit der sog. Pulsfläche $\Theta$ mit

$\Theta (t)=\int \limits _{t_{0}}^{t}\underbrace {\frac {|d_{12}|{\mathcal {E}}(t')}{\hbar }} _{\Omega _{R}}\mathrm {d} t'$

Somit führen $\Delta n$ und ${\mathcal {P}}$ Schwingungen aus, die vom elektrischen Feld getrieben werden. Dies nennt man Rabi-Oszillationen. Mit der dritten Maxwell-Bloch-Gleichung findet man, unter der Annahme einer dünnen Probe der Länge L, d. h. $\tau _{p}\gg {\frac {L}{c_{g}}}$, für das reemittierte elektrische Feld

${\mathcal {E}}_{\text{out}}(t)={\mathcal {E}}(t)-{\frac {n_{0}|d_{12}|}{2\varepsilon _{0}}}kL{\frac {c_{p}}{c}}\sin(\Theta (t)).$

Wenn man nun einen eingehenden Lichtpuls so präpariert, dass $\Theta (t\rightarrow \infty )=2\pi m+\pi$ mit $m\in \mathbb {Z}$ kann man das Medium vollständig invertieren. Man spricht dann von einem $\pi$-Puls (siehe Abbildung). Für $\Theta (t\rightarrow \infty )=2\pi m+{\frac {\pi }{2}}$ ist die Besetzungsinversion null und die Polarisation ist maximal. Mit dieser Methode kann man also ein Material in einen genau definierten Zustand bringen.

Herleitung

Zur Herleitung der Maxwell-Bloch-Gleichungen beschreibt man die Wechselwirkung zwischen elektrischem Feld und Atom in der sog. Dipolnäherung. Der Hamilton-Operator des Systems besteht aus zwei Anteilen. Dem Anteil ${\hat {H}}_{0}$ der das Atom ohne Wechselwirkung mit dem elektrischen Feld beschreibt und dem Anteil ${\hat {H}}^{\text{ww}}$ der eine dipolartige Wechselwirkung zwischen Licht und Atom beschreibt:

${\hat {H}}={\hat {H}}_{0}+{\hat {H}}^{\text{ww}}$

mit

${\hat {H}}^{\text{ww}}={\vec {E}}(t)\cdot {\vec {\hat {d}}}=-e\;{\vec {E}}\cdot {\vec {\hat {r}}}.$

Die Wellenfunktion $|\Psi \rangle$ kann in der Basis $|\varphi _{k}\rangle$ des ungestörten Systems als

$|\Psi \rangle =c_{1}(t)e^{-i\omega _{1}t}|\varphi _{1}\rangle +c_{2}(t)e^{-i\omega _{2}t}|\varphi _{2}\rangle$

dargestellt werden. Die Schrödingergleichung lautet nun

$i\hbar \partial _{t}|\Psi \rangle =\left({\hat {H}}_{0}+{\hat {H}}^{\text{ww}}\right)|\Psi \rangle .$

Durch Multiplikation mit $\langle \varphi _{m}|e^{i\omega _{m}t}$ und Einsetzen der Basisdarstellung von $|\Psi \rangle$ folgt

$i\hbar {\dot {c}}_{1}=-d_{12}E(t)e^{-i\Omega t}c_{2}$

$i\hbar {\dot {c}}_{2}=-d_{12}^{\star }E(t)e^{i\Omega t}c_{1}$

Dabei wurde $d_{11}=d_{22}=0$ ausgenutzt. Die mikroskopische Polarisation ${\vec {P}}$ des Systems ist nun durch

${\vec {P}}=n_{0}\langle \Psi |-e{\vec {r}}|\Psi \rangle =\underbrace {-d_{12}e^{i\Omega t}c_{1}^{\star }c_{2}n_{0}{\vec {e}}_{\vec {E}}} _{={\vec {P}}^{+}}+\underbrace {\text{c.c.}} _{={\vec {P}}^{-}}$

gegeben. Für die zeitlichen Ableitungen der Polarisationskomponenten ${\vec {P}}^{+}$ und ${\vec {P}}^{-}$ folgt

${\begin{aligned}\partial _{t}{\vec {P}}^{+}&=-d_{12}e^{i\Omega t}n_{0}{\vec {e}}_{\vec {E}}\left(i\Omega c_{1}^{\star }c_{2}+{\dot {c}}_{1}^{\star }c_{2}+c_{1}^{\star }{\dot {c}}_{2}\right)\\&=i\Omega {\vec {P}}^{+}-{\frac {i}{\hbar }}|d_{12}|^{2}E(t)\underbrace {n_{0}\left(|c_{1}|^{2}-|c_{2}|^{2}\right)} _{=-\Delta n}.\end{aligned}}$

Dabei wurden die Gleichungen

${\dot {c}}_{1}^{\star }c_{2}=-{\frac {i}{\hbar }}d_{12}^{\star }E(t)e^{i\Omega t}|c_{2}|^{2}$

$c_{1}^{\star }{\dot {c}}_{2}={\frac {i}{\hbar }}d_{12}^{\star }E(t)e^{i\Omega t}|c_{1}|^{2}$

verwendet. Die Gleichung für ${\vec {P}}^{-}$ ergibt sich einfach aus der komplex konjugierten Gleichung.

$\partial _{t}{\vec {P}}^{-}=(\partial _{t}{\vec {P}}^{+})^{\star }$

Für den feldfreien Fall ($E=0$) schwingt die Polarisation nun harmonisch. In realen System klingt die Polarisation allerdings ab, weshalb man einen Zerfallsterm ${\frac {-{\vec {P}}}{\tau _{p}}}$ addiert. Die Materialkonstante $\tau _{p}$ nennt man dabei Phasenrelaxationszeit. Weiterhin verwendet man die sog. Rotating Wave Näherung. Dabei setzt man

${\vec {E}}=\underbrace {{\mathcal {E}}(t,z)e^{i(kz-\omega t)}} _{{\vec {E}}^{+}}+\underbrace {{\mathcal {E}}^{\star }(t,z)e^{-i(kz-\omega t)}} _{{\vec {E}}^{-}}$

und vernachlässigt ${\vec {E}}^{-}$ in der Gleichung für ${\vec {P}}^{+}$ und entsprechend ${\vec {E}}^{+}$ in der Gleichung für ${\vec {P}}^{-}$, da die vernachlässigten Terme mit $\omega +\Omega$ oszillieren und somit im Vergleich zu den Termen mit $\omega -\Omega$ klein sind. Für die Polarisation folgt somit

$\partial _{t}{\vec {P}}^{\pm }=\left(\mp i\Omega -{\frac {1}{\tau _{p}}}\right){\vec {P}}^{\pm }+{\frac {|d_{12}|^{2}}{i\hbar }}\Delta n\cdot {\vec {E}}^{\pm }$

was durch den Ansatz ${\vec {P}}^{+}={\mathcal {P}}(z,t)\cdot e^{i(kz-\omega t)}$ noch zu

$\partial _{t}{\mathcal {P}}=\left(i\Omega -{\frac {1}{\tau _{p}}}\right){\mathcal {P}}+{\frac {|d_{12}|^{2}}{i\hbar }}\Delta n\cdot {\mathcal {E}}$

vereinfacht werden kann. Für die Zeitableitung der Besetzungsinversion folgt

${\begin{aligned}\partial _{t}\Delta n&=2\partial _{t}n_{2}=2n_{0}\left({\dot {c}}_{2}^{\star }c_{2}+c_{2}^{\star }{\dot {c}}_{2}\right)\\&={\frac {4}{\hbar }}{\text{Im}}({\vec {E}}^{-}{\vec {P}}^{+})={\frac {4}{\hbar }}{\text{Im}}({\mathcal {E}}^{\star }{\mathcal {P}})\end{aligned}}$

Auch hierbei würde im feldfreien Fall $(E=P=0)$ die Besetzungsinversion konstant bleiben, weshalb man einen Term mit $-{\frac {n_{2}}{\tau }}=-{\frac {n_{0}+\Delta n}{\tau }}$ addiert.

$\partial _{t}\Delta n={\frac {4}{\hbar }}{\text{Im}}({\mathcal {E}}^{\star }{\mathcal {P}})-{\frac {n_{0}+\Delta n}{\tau }}$

Dabei ist $\tau$ die mittlere Lebensdauer des angeregten Zustandes. Zuletzt braucht man noch eine Gleichung für das elektrische Feld. Dabei geht man von der Wellengleichung

$\partial _{z}^{2}{\vec {E}}-{\frac {1}{c_{p}^{2}}}\partial _{t}^{2}\varepsilon {\vec {E}}=-\mu _{0}\partial _{t}^{2}{\vec {P}}$

aus. Durch Einsetzen der schon erhaltenen Zusammenhänge und Ansätze folgt

$\partial _{z}^{2}{\vec {E}}^{+}=\left(\partial _{z}^{2}{\mathcal {E}}+2ik\partial _{z}{\mathcal {E}}-k^{2}{\mathcal {E}}\right)\cdot e^{i(kz-\omega t)}$

${\frac {1}{c^{2}}}\partial _{t}^{2}\varepsilon {\vec {E}}^{+}\approx -\left(k^{2}{\mathcal {E}}+{\frac {2ik}{c_{g}}}\partial _{t}{\mathcal {E}}\right)\cdot e^{i(kz-\omega t)}$

$\partial _{t}^{2}{\vec {P}}^{+}=\left(-\omega ^{2}{\mathcal {P}}-2i\omega \partial _{t}{\mathcal {P}}+\partial _{t}^{2}{\mathcal {P}}\right)\cdot e^{i(kz-\omega t)}\approx -\omega ^{2}{\mathcal {P}}\cdot e^{i(kz-\omega t)}$

und damit die letzte Maxwell-Bloch-Gleichung

$\left(\partial _{z}+{\frac {1}{c_{g}}}\partial _{t}\right){\mathcal {E}}={\frac {i}{2}}\mu _{0}c_{p}{\mathcal {P}}$

Literatur

• Dieter Meschede: Optik, Licht und Laser. Vieweg+Teubner Verlag; 3., durchges. Aufl. 2008. ISBN 978-3-8351-0143-2