Miura-Faltung
Die Miura-Faltung (japanisch ミウラ折り Miura-ori) ist eine Methode, ein flaches Objekt in eine kleinere Oberfläche zu falten. Die Faltung ist nach ihrem Erfinder, dem japanischen Astrophysiker Koryo Miura benannt.[1] Die besondere Faltung erlaubt es, das Objekt durch eine kontinuierliche Bewegung in nur eine Richtung vollständig zu entfalten.
Faltmuster
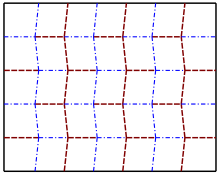
[Bearbeiten | Quelltext bearbeiten]Das Faltmuster besteht dabei aus einer Tessellation mit Parallelogrammen, deren Kanten in eine Richtung gerade Linien und in die andere Richtung ein „Zickzackmuster“ bilden. Jedes Parallelogramm ist dabei bezüglich der geraden Linie zu dem benachbarten Parallelogramm achsensymmetrisch. Jeder Schnittpunkt von Falten grenzt dabei an drei Talfalten und eine Bergfalte beziehungsweise an drei Bergfalten und eine Talfalte.
Verwendung
[Bearbeiten | Quelltext bearbeiten]
Als technisches Origami findet die Faltung vor allem in der Raumfahrt Verwendung – durch die besonderen Eigenschaften können Solarmodule effizient transportiert und mit nur einem Motor entfaltet werden. Beispielsweise nutzte die Space Flyer Unit im Jahr 1996[2] oder auch der SPROUT Satellit das beschriebene Prinzip.
Weitere Anwendungsfelder umfassen komfortabel zu nutzende Karten und potentiell faltbare Möbel.[3]
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Peter Forbes: The Gecko’s Foot: How Scientists are Taking a Leaf from Nature’s Book. Harper Perennial, London 2006, ISBN 0-00-717989-8, S. 181–195.
- ↑ Institute of Space and Astronautical Science. Jaxa, 25. November 2005, archiviert vom (nicht mehr online verfügbar) am 25. November 2005; abgerufen am 9. Juni 2017.
- ↑ Designing a pop-up future: Simple origami fold may hold the key to designing pop-up furniture, medical devices and scientific tools. In: ScienceDaily. (sciencedaily.com [abgerufen am 9. Juni 2017]).