Die NLC-Weite ist ein Begriff aus der Graphentheorie und weist jedem ungerichteten Graphen eine natürliche Zahl zu. Auf Graphen mit beschränkter NLC-Weite lassen sich bestimmte schwere Probleme
wie zum Beispiel MAX-CUT oder das Hamiltonkreisproblem in polynomieller Zeit lösen.
Der Begriff der NLC-Weite wurde von 1994 von Wanke eingeführt[ 1] k-markierten Graphen wichtig:
Für ein
k
∈
N
{\displaystyle \,k\in \mathbb {N} }
[
k
]
:=
{
1
,
…
,
k
}
{\displaystyle \lbrack k\rbrack \,:=\lbrace 1,\ldots ,k\rbrace }
Ein k-markierter Graph
G
=
(
V
G
,
E
G
,
l
a
b
G
)
{\displaystyle \ G=(V_{G},E_{G},lab_{G})\ }
(
V
G
,
E
G
)
{\displaystyle \ (V_{G},E_{G})\ }
l
a
b
G
:
V
G
→
[
k
]
{\displaystyle \,lab_{G}:V_{G}\rightarrow \lbrack k\rbrack }
Ein Graph mit genau einem mit
i
∈
[
k
]
{\displaystyle i\in \lbrack k\rbrack }
∙
i
{\displaystyle \bullet _{i}}
Die NLC-Weite eines k-markierten Graphen
G
{\displaystyle G}
k
,
{\displaystyle k,}
G
{\displaystyle G}
Graphklasse
N
L
C
k
{\displaystyle NLC_{k}}
Dabei ist
N
L
C
k
{\displaystyle NLC_{k}}
Der
k
{\displaystyle k}
∙
i
{\displaystyle \bullet _{i}}
i
∈
[
k
]
{\displaystyle i\in \lbrack k\rbrack }
N
L
C
k
{\displaystyle NLC_{k}}
Seien
G
=
(
V
G
,
E
G
,
l
a
b
G
)
{\displaystyle G=(V_{G},E_{G},lab_{G})}
J
=
(
V
J
,
E
J
,
l
a
b
J
)
{\displaystyle J=(V_{J},E_{J},lab_{J})}
N
L
C
k
{\displaystyle NLC_{k}}
G
{\displaystyle G}
J
{\displaystyle J}
S
⊆
[
k
]
2
{\displaystyle S\subseteq \lbrack k\rbrack ^{2}}
k
{\displaystyle k}
G
×
S
J
=
(
V
′
,
E
′
,
l
a
b
′
)
{\displaystyle G\times _{S}J=(V',E',lab')}
in
N
L
C
k
{\displaystyle NLC_{k}}
V
′
=
V
G
∪
V
J
{\displaystyle V'=V_{G}\cup V_{J}}
E
′
=
E
G
∪
E
J
∪
{
{
u
,
v
}
|
u
∈
V
G
,
v
∈
V
J
,
(
l
a
b
G
(
u
)
,
l
a
b
J
(
v
)
)
∈
S
}
{\displaystyle E'=E_{G}\cup E_{J}\cup \lbrace \lbrace u,v\rbrace |u\in V_{G},v\in V_{J},(lab_{G}(u),lab_{J}(v))\in S\rbrace }
l
a
b
′
(
u
)
=
{
l
a
b
G
(
u
)
,
falls
u
∈
V
G
l
a
b
J
(
u
)
,
falls
u
∈
V
J
{\displaystyle lab'(u)={\begin{cases}lab_{G}(u),&{\text{falls }}u\in V_{G}\\lab_{J}(u),&{\text{falls }}u\in V_{J}\end{cases}}}
für alle
u
∈
V
′
{\displaystyle u\in V'}
Seien
G
=
(
V
G
,
E
G
,
l
a
b
G
)
∈
N
L
C
k
{\displaystyle G=(V_{G},E_{G},lab_{G})\in NLC_{k}}
k
{\displaystyle k}
R
:
[
k
]
→
[
k
]
{\displaystyle R:\lbrack k\rbrack \rightarrow \lbrack k\rbrack }
k
{\displaystyle k}
∘
R
(
G
)
=
(
V
G
,
E
G
,
l
a
b
′
)
{\displaystyle \circ _{R}(G)=(V_{G},E_{G},lab')}
in
N
L
C
k
{\displaystyle NLC_{k}}
l
a
b
′
(
u
)
=
R
(
l
a
b
(
u
)
)
∀
u
∈
V
G
{\displaystyle lab'(u)=R(lab(u))\qquad \forall u\in V_{G}}
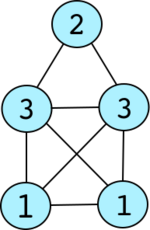
Die nachfolgende Tabelle demonstriert die Konstruktion des "Haus vom Nikolaus"-Graphen mithilfe der oben definierten Operationen:
NLC-Operation
Darstellung des Graphen
G
1
=
∙
1
×
{
(
1
,
2
)
}
∙
2
{\displaystyle G_{1}=\bullet _{1}\times _{\lbrace (1,2)\rbrace }\bullet _{2}}
G
2
=
∙
3
×
{
(
3
,
4
)
}
∙
4
{\displaystyle G_{2}=\bullet _{3}\times _{\lbrace (3,4)\rbrace }\bullet _{4}}
G
3
=
G
1
×
{
(
1
,
3
)
,
(
1
,
4
)
,
(
2
,
3
)
,
(
2
,
4
)
}
G
2
{\displaystyle G_{3}=G_{1}\times _{\lbrace (1,3),(1,4),(2,3),(2,4)\rbrace }G_{2}}
G
4
=
∘
{
(
1
,
1
)
,
(
2
,
1
)
,
(
3
,
3
)
,
(
4
,
3
)
}
(
G
3
)
{\displaystyle G_{4}=\circ _{\lbrace (1,1),(2,1),(3,3),(4,3)\rbrace }(G_{3})}
G
N
i
k
o
l
a
u
s
=
G
4
×
{
(
3
,
2
)
}
∙
2
{\displaystyle G_{Nikolaus}=G_{4}\times _{\lbrace (3,2)\rbrace }\bullet _{2}}
Es gilt somit
G
N
i
k
o
l
a
u
s
∈
N
L
C
4
{\displaystyle G_{Nikolaus}\in NLC_{4}}
G
N
i
k
o
l
a
u
s
{\displaystyle G_{Nikolaus}}
G
N
i
k
o
l
a
u
s
{\displaystyle G_{Nikolaus}}
Co-Graph ist.
Die NLC-Weiten der folgenden Graphklassen lassen sich wie folgt nach oben abschätzen:
Jeder Co-Graph hat eine NLC-Weite von 1
Bäume haben eine NLC-Weite von höchstens 3Kreise haben eine NLC-Weite von höchstens 4Für jeden ungerichteten Graphen
G
{\displaystyle G}
n
l
c
w
(
G
)
{\displaystyle nlcw(G)}
Cliquenweite
c
w
(
G
)
{\displaystyle cw(G)}
n
l
c
w
(
G
)
≤
c
w
(
G
)
≤
2
⋅
n
l
c
w
(
G
)
.
{\displaystyle nlcw(G)\leq cw(G)\leq 2\cdot nlcw(G).}
Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme , Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1
↑ Egon Wanke: k -NLC Graphs and Polynomial Algorithms, Discrete Applied Mathematics, 54:251-266, 1994