Nevillesche Thetafunktionen

Die Nevilleschen Thetafunktionen bilden in der Mathematik eine infinitesimalanalytische Funktionengruppe, welche zu den Elliptischen Funktionen zählt. Sie wurden nach dem englischen Mathematiker Eric Harold Neville benannt. Akkurat sind die Nevilleschen Thetafunktionen die Quotienten der Jacobischen Thetafunktionen dividiert durch ihre zugehörigen Theta-Nullwert-Funktionen mit dem Elliptischen Nomen von der korrespondierenden numerischen Exzentrizität als zugehöriger Nomeneintrag. Rationale Kombinationen aus den Nevilleschen Thetafunktionen bauen direkt die Jacobischen Amplitudenfunktionen auf, während umgekehrt dieser Vorgang nicht möglich ist.

Definitionen

Definitionen von Nomen und K-Integral

Definitionen der Standardformen

Als Erstes wird das vollständige elliptische Integral erster Art in seiner Standardform definiert:

$K(\varepsilon )=\int _{0}^{1}{\frac {2}{\sqrt {(x^{2}+1)^{2}-4\,\varepsilon ^{2}x^{2}}}}\,\mathrm {d} x$

$K'(\varepsilon )=\int _{0}^{1}{\frac {2}{\sqrt {(x^{2}-1)^{2}+4\,\varepsilon ^{2}x^{2}}}}\,\mathrm {d} x$

Das komplementäre Integral $K'$ ist gleich dem K-Integral vom pythagoräisch komplementären Modul:

$K'(k)=K({\sqrt {1-k^{2}}}\,)$

Basierend darauf wird das Elliptische Nomen in seiner Standardform so definiert:

$q(k)=\exp {\bigl [}-\pi \,K'(k)\div K(k){\bigr ]}$

Das Elliptische Nomen ist gleich dem Exponentialfunktionswert aus dem negativen Kreiszahlfachen des Periodenverhältnisses.

Definitionen der reduzierten Formen

Als Nächstes wird das reduzierte vollständige elliptische Integral erster Art und das reduzierte elliptische Nomen definiert:

${\bar {K}}(k)={\frac {2}{\pi }}K(k)=1+\sum _{n=1}^{\infty }\,{\frac {\operatorname {CBC} (n)^{2}}{16^{n}}}\,k^{2n}$

${\bar {q}}(k)={\sqrt[{4}]{k^{-2}q(k)}}={\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n+1)}{2^{4n+1}}}k^{2n}{\biggr ]}$

Die nun beschriebenen jeweiligen reduzierten Formen werden mit einem Querbalken über den betroffenen Buchstaben dargestellt.

Der Ausdruck $\mathrm {CBC}$ stellt den Zentralbinomialkoeffizienten dar:

$\operatorname {CBC} (n)=(2n)!\div (n!)^{2}=\Pi (2n)\div \Pi (n)^{2}$

Das Kürzel $\mathrm {Sc}$ drückt die Schellbachsche Zahlenfolge aus.

Erzeugungsalgorithmen der Zahlenfolgen

Die Schellbachsche Zahlenfolge (A002103) kann mit der Kneserschen Zahlenfolge (A227503) erzeugt werden.

Diese Tabelle stellt die beiden Folgen exemplarisch dar:

Index	1	2	3	4	5	6	7	8	9
Schellbach-Zahl	1	2	15	150	1707	20910	268616	3567400	48555069
Kneser-Zahl	1	13	184	2701	40456	613720	9391936	144644749	2238445480

Ein Erzeugungsalgorithmus für die Schellbachsche Zahlenfolge soll im nun Folgenden exemplarisch zusammengefasst werden:

Zuerst wird die Kneserschen Zahlenfolge erzeugt:

${\text{Kn}}(2n)=2^{4n-3}{\binom {4n}{2n}}+\sum _{m=1}^{n}4^{2n-2m}{\binom {4n}{2n-2m}}{\text{Kn}}(m)$

${\text{Kn}}(2n+1)=2^{4n-1}{\binom {4n+2}{2n+1}}+\sum _{m=1}^{n}4^{2n-2m+1}{\binom {4n+2}{2n-2m+1}}{\text{Kn}}(m)$

Basierend auf dem gegebenen Wert Kn(1) = 1 können jetzt diese ausgeführten Beispiele generiert werden:

${\text{Kn}}(2)=2\times 6+1\times {\color {cornflowerblue}1}={\color {cornflowerblue}13}$

${\text{Kn}}(3)=8\times 20+24\times {\color {cornflowerblue}1}={\color {cornflowerblue}184}$

${\text{Kn}}(4)=32\times 70+448\times {\color {cornflowerblue}1}+1\times {\color {cornflowerblue}13}={\color {cornflowerblue}2701}$

${\text{Kn}}(5)=128\times 252+7680\times {\color {cornflowerblue}1}+40\times {\color {cornflowerblue}13}={\color {cornflowerblue}40456}$

${\text{Kn}}(6)=512\times 924+126720\times {\color {cornflowerblue}1}+1056\times {\color {cornflowerblue}13}+1\times {\color {cornflowerblue}184}={\color {cornflowerblue}613720}$

${\text{Kn}}(7)=2048\times 3432+2050048\times {\color {cornflowerblue}1}+23296\times {\color {cornflowerblue}13}+56\times {\color {cornflowerblue}184}={\color {cornflowerblue}9391936}$

Die Erzeugende Funktion der Kneserschen Zahlenfolge Kn(n) ist die Funktion des elliptischen Periodenverhältnisses:

${\frac {1}{4}}\ln {\bigl (}{\frac {16}{x^{2}}}{\bigr )}-{\frac {\pi \,K'(x)}{4\,K(x)}}=\sum _{n=1}^{\infty }{\frac {{\text{Kn}}(n)}{2^{4n-1}n}}\,x^{2n}$

${\color {limegreen}{\frac {1}{4}}\ln {\bigl (}{\frac {16}{x^{2}}}{\bigr )}-{\frac {\pi \,K'(x)}{4\,K(x)}}={\frac {\color {cornflowerblue}1}{8}}x^{2}+{\frac {\color {cornflowerblue}13}{256}}x^{4}+{\frac {\color {cornflowerblue}184}{6144}}x^{6}+{\frac {\color {cornflowerblue}2701}{131072}}x^{8}+{\frac {\color {cornflowerblue}40456}{2621440}}x^{10}+\ldots }$

Die Knesersche Folge erscheint ebenso in der Reihenentwicklung der folgenden Funktion:

${\frac {\pi ^{2}}{8x(1-x^{2})K(x)^{2}}}-{\frac {1}{2x}}=\sum _{n=1}^{\infty }{\frac {{\text{Kn}}(n)}{2^{4n-2}}}x^{2n-1}$

Das ist die Ableitung der zuvor gezeigten Periodenverhältnis-Funktion.

Nun wird auf Grundlage der Kneserschen Folge die Schellbachsche Folge hervorgerufen.

Dies funktioniert mit folgender Erzeugungsformel:

${\text{Sc}}(n+1)={\frac {2}{n}}\sum _{m=1}^{n}{\text{Sc}}(m){\text{Kn}}(n+1-m)$

So werden die Beispiele erzeugt:

$\mathrm {Sc} (4)={\frac {2}{3}}\sum _{m=1}^{3}\mathrm {Sc} (m)\,\mathrm {Kn} (4-m)={\frac {2}{3}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}$

${\color {navy}\mathrm {Sc} (4)}={\frac {2}{3}}{\bigl (}{\color {navy}1}\times {\color {cornflowerblue}184}+{\color {navy}2}\times {\color {cornflowerblue}13}+{\color {navy}15}\times {\color {cornflowerblue}1}{\bigr )}={\color {navy}150}$

$\mathrm {Sc} (5)={\frac {2}{4}}\sum _{m=1}^{4}\mathrm {Sc} (m)\,\mathrm {Kn} (5-m)={\frac {2}{4}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}$

${\color {navy}\mathrm {Sc} (5)}={\frac {2}{4}}{\bigl (}{\color {navy}1}\times {\color {cornflowerblue}2701}+{\color {navy}2}\times {\color {cornflowerblue}184}+{\color {navy}15}\times {\color {cornflowerblue}13}+{\color {navy}150}\times {\color {cornflowerblue}1}{\bigr )}={\color {navy}1707}$

$\mathrm {Sc} (6)={\frac {2}{5}}\sum _{m=1}^{5}\mathrm {Sc} (m)\,\mathrm {Kn} (6-m)={\frac {2}{5}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (5)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (5)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}$

${\color {navy}\mathrm {Sc} (6)}={\frac {2}{5}}{\bigl (}{\color {navy}1}\times {\color {cornflowerblue}40456}+{\color {navy}2}\times {\color {cornflowerblue}2701}+{\color {navy}15}\times {\color {cornflowerblue}184}+{\color {navy}150}\times {\color {cornflowerblue}13}+{\color {navy}1707}\times {\color {cornflowerblue}1}{\bigr )}={\color {navy}20910}$

So wird diese Zahlenfolge nach Karl Heinrich Schellbach und Hermann Amandus Schwarz für die Erzeugung des elliptischen Nomens verwendet:

$q(k)=k^{2}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n+1)}{2^{4n+1}}}k^{2n}{\biggr ]}{\biggr \}}^{4}$

Ebenso gültig ist folgender Ausdruck, welcher durch zweifache Durchführung der Landenschen Transformation hervorgeht:

$q(k)=\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n)}{2^{4n-3}}}{\biggl (}{\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}}{\biggr )}^{4n-3}$

Definitionen der Nevilleschen Funktionen

Definition über Jacobische Thetafunktionen

Nach Edmund Taylor Whittaker und George Neville Watson sind die Neville Thetafunktionen ganz genau so als Quotienten aus Jacobischer Thetafunktion und Theta-Nullwert definiert:

$\theta _{c}(z;k)=\vartheta _{10}{\bigl [}q(k){\bigr ]}^{-1}\vartheta _{10}{\bigl [}z\div {\bar {K}}(k);q(k){\bigr ]}=\cos {\bigl [}z\div {\bar {K}}(k){\bigr ]}\prod _{n=1}^{\infty }{\bigl [}1+q(k)^{2n}{\bigr ]}^{-2}{\bigl \{}1+2q(k)^{2n}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n}{\bigr \}}$

$\theta _{d}(z;k)=\vartheta _{00}{\bigl [}q(k){\bigr ]}^{-1}\vartheta _{00}{\bigl [}z\div {\bar {K}}(k);q(k){\bigr ]}=\prod _{n=1}^{\infty }{\bigl [}1+q(k)^{2n-1}{\bigr ]}^{-2}{\bigl \{}1+2q(k)^{2n-1}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n-2}{\bigr \}}$

$\theta _{n}(z;k)=\vartheta _{01}{\bigl [}q(k){\bigr ]}^{-1}\vartheta _{01}{\bigl [}z\div {\bar {K}}(k);q(k){\bigr ]}=\prod _{n=1}^{\infty }{\bigl [}1-q(k)^{2n-1}{\bigr ]}^{-2}{\bigl \{}1-2q(k)^{2n-1}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n-2}{\bigr \}}$

$\theta _{s}(z;k)={\bar {K}}(k)\sin {\bigl [}z\div {\bar {K}}(k){\bigr ]}\prod _{n=1}^{\infty }{\bigl [}1-q(k)^{2n}{\bigr ]}^{-2}{\bigl \{}1-2q(k)^{2n}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n}{\bigr \}}$

Definition über Lambertsche Reihen

So sind die Nevilleschen Thetafunktionen über die Lambertschen Reihen definiert:

$\theta _{c}(z;k)=2\,{\bar {q}}(k)\,{\bar {K}}(k)^{-1/2}\,\sum _{n=1}^{\infty }q(k)^{n(n-1)}\cos {\bigl [}(2n-1){\bar {K}}(k)^{-1}z{\bigr ]}$

$\theta _{d}(z;k)={\bar {K}}(k)^{-1/2}\,{\biggl \{}1+2\,\sum _{n=1}^{\infty }q(k)^{n^{2}}\cos {\bigl [}2\,n\,{\bar {K}}(k)^{-1}z{\bigr ]}{\biggr \}}$

$\theta _{n}(z;k)=(1-k^{2})^{-1/4}{\bar {K}}(k)^{-1/2}\,{\biggl \{}1+2\,\sum _{n=1}^{\infty }(-1)^{n}q(k)^{n^{2}}\cos {\bigl [}2\,n\,{\bar {K}}(k)^{-1}z{\bigr ]}{\biggr \}}$

$\theta _{s}(z;k)=2\,(1-k^{2})^{-1/4}{\bar {q}}(k)\,{\bar {K}}(k)^{-1/2}\,\sum _{n=1}^{\infty }(-1)^{n-1}q(k)^{n(n-1)}\sin {\bigl [}(2n-1){\bar {K}}(k)^{-1}z{\bigr ]}$

Definition über Exponentialreihen

Sehr schnell konvergent sind folgende Summenreihen für die Nevilleschen Thetafunktionen:

$\theta _{c}(z;k)=|k|^{-1/2}{\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }(-1)^{n}\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}$

$\theta _{d}(z;k)={\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}$

$\theta _{n}(z;k)=(1-k^{2})^{-1/4}{\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {1}{2}}+{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}$

$\theta _{s}(z;k)=|k|^{-1/2}(1-k^{2})^{-1/4}{\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }(-1)^{n}\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {1}{2}}-{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}$

Definition über die Ramanujansche Thetafunktion

So wird die Ramanujansche Thetafunktion definiert:

$\vartheta _{R}(v;w)=\sum _{n=-\infty }^{\infty }v^{n(n+1)/2}\,w^{n(n-1)/2}=\sum _{n=-\infty }^{\infty }v^{\bigtriangleup (n)}\,w^{\bigtriangleup (n-1)}$

$\vartheta _{R}(v;w)=1+v+w+\sum _{n=1}^{\infty }(vw)^{\bigtriangleup (n)}(v^{n+1}+w^{n+1})$

$\vartheta _{R}(v;w)=(-v;vw)_{\infty }(-w;vw)_{\infty }(vw;vw)_{\infty }$

$\vartheta _{R}(v;w)=1+{\frac {2v}{\sqrt {\pi }}}\int _{0}^{\infty }\exp(-x^{2}){\biggl \{}{\frac {1-v{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}}{1-2v{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}+v^{3}w}}{\biggr \}}\,\mathrm {d} x\,+$

$+\,{\frac {2w}{\sqrt {\pi }}}\int _{0}^{\infty }\exp(-x^{2}){\biggl \{}{\frac {1-w{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}}{1-2w{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}+vw^{3}}}{\biggr \}}\,\mathrm {d} x$

Die Dreieckssymbole in den Exponenten der beiden obersten Formeln dieser Liste stellen die Funktion von der Folge der Dreieckszahlen dar. Durch die Tatsache, dass sich die Exponenten in den genannten Summenreihen bezüglich des Index in der Funktion der Dreieckszahlen verhalten, konvergieren die gezeigten Summenreihen sehr schnell mit einem quadratischen Wachstum der richtigen Nachkommastellen. Mit dem Unendlichkeitssymbol in Basislage wird das Nomen-Pochhammer-Produkt dargestellt, welches die unendliche Variante des verallgemeinerten Pochhammer-Produktes ist. Die am Ende dieser Liste dargestellten Integrale von Produkten aus Gaussscher Glockenkurvenfunktion und trigonometrischem Funktionenbruch wurden in der Universität Georgia durch die kanadische Mathematikerin Maxie Schmidt und ihre Arbeitsgruppe erforscht und beschreiben sogenannte uneigentliche Integrale. Die Nevillesche Thetafunktion $\theta _{d}$ kann mit Hilfe der Ramanujanschen Thetafunktion auf diese Weise dargestellt werden:

$\theta _{d}(z;k)={\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\exp {\biggl [}-{\frac {\pi \,z^{2}}{4\,K(k)\,K'(k)}}{\biggr ]}\vartheta _{R}{\biggl \{}\exp {\biggl [}\pi \,{\frac {z-K(k)}{K'(k)}}{\biggr ]};\exp {\biggl [}\pi \,{\frac {-z-K(k)}{K'(k)}}{\biggr ]}{\biggr \}}$

Umgekehrt gilt dementsprechend:

$\vartheta _{R}(v;w)=\exp {\biggl [}-{\frac {\ln(v\div w)^{2}}{8\ln(vw)}}{\biggr ]}\vartheta _{00}({\sqrt {vw}}\,)\,\theta _{d}{\bigl [}{\frac {1}{4}}\ln(v\div w)\vartheta _{00}({\sqrt {vw}}\,)^{2};\psi _{H}({\sqrt {vw}}\,)^{4}{\bigr ]}$

Sukzessiv kann darauf zu dieser Nevilleschen Thetafunktion geführt werden:

$\theta _{n}(z;k)=(1-k^{2})^{-1/4}\theta _{d}{\bigl [}K(k)-z;k{\bigr ]}$

Beispielwerte

Lemniskatische Beispielwerte

Im Folgenden werden die zugehörigen Werte in Kombination mit dem lemniskatisch elliptischen Modul $k=\lambda ^{*}(1)={\tfrac {1}{2}}{\sqrt {2}}$ niedergeschrieben:

Werte für $\theta _{c}$:

$\theta _{c}{\bigl [}{\tfrac {1}{2}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-3/16}{\sqrt[{4}]{{\sqrt {2}}-1}}$

$\theta _{c}{\bigl [}{\tfrac {1}{3}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/4}3^{1/8}(2+{\sqrt {3}}\,)^{-1/12}$

Werte für $\theta _{d}$:

$\theta _{d}{\bigl [}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/4}$

$\theta _{d}{\bigl [}{\tfrac {1}{2}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-7/16}{\sqrt[{4}]{{\sqrt {2}}+1}}$

$\theta _{d}{\bigl [}{\tfrac {2}{3}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/2}{\sqrt[{6}]{2+{\sqrt {3}}}}$

$\theta _{d}{\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/2}{\sqrt[{5}]{2({\sqrt {5}}+2)\cos({\tfrac {1}{20}}\pi )\tan({\tfrac {3}{20}}\pi )}}$

$\theta _{d}{\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/2}{\sqrt[{5}]{2({\sqrt {5}}+2)\sin({\tfrac {1}{20}}\pi )\cot({\tfrac {3}{20}}\pi )}}$

Nicht lemniskatische Beispielwerte

Werte für Modul λ*(2)

Diese Werte kommen durch Einsatz vom Modul $\lambda ^{*}(2)={\sqrt {2}}-1$ hervor:

$\theta _{d}{\bigl [}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{1/4}({\sqrt {2}}+1)^{-1/4}$

$\theta _{d}{\bigl [}{\tfrac {1}{3}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{-1/4}({\sqrt {2}}+1)^{-1/4}({\sqrt {3}}+{\sqrt {2}}\,)^{1/3}$

$\theta _{d}{\bigl [}{\tfrac {2}{3}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=\sec({\tfrac {1}{8}}\pi )\sin({\tfrac {5}{24}}\pi )({\sqrt {3}}+{\sqrt {2}}\,)^{1/3}$

$\theta _{n}{\bigl [}{\tfrac {2}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{-1/2}{\text{g}}(50)^{1/2}\tan {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{1/10}\cot {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{3/10}$

$\theta _{n}{\bigl [}{\tfrac {4}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{-1/2}{\text{g}}(50)^{1/2}\cot {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{1/10}\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{3/10}$

Dabei steht ${\text{g}}(50)$ für folgende Konstante:

${\text{g}}(50)=w_{R5}({\sqrt {2}}-1)=2\,[\exp(-5\,{\sqrt {2}}\,\pi );\exp(-10\,{\sqrt {2}}\,\pi )]_{\infty }[\exp(-{\sqrt {2}}\,\pi );\exp(-2\,{\sqrt {2}}\,\pi )]_{\infty }^{-5}=$

$={\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi ){\bigr \}}^{2}-{\tfrac {1}{2}}=$

$={\bigl \langle }{\tfrac {1}{2}}-{\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\sin({\tfrac {1}{5}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]-{\tfrac {1}{3}}\cot({\tfrac {1}{10}}\pi ){\bigr \}}^{2}{\bigr \rangle }^{-1}=$

$=\Phi ^{-1}\cot {\bigl [}{\tfrac {1}{4}}\pi -\arctan {\bigl (}{\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}{\bigr )}{\bigr ]}=$

$\approx 2{,}12190403802900202926$

Zugehörige Gleichungen:

${\text{g}}(50)^{6}-2\,{\text{g}}(50)^{5}-2\,{\text{g}}(50)-1=0$

${\text{g}}(50)^{3}-{\text{g}}(50)^{2}-\Phi \,{\text{g}}(50)-\Phi =0$

Werte für Modul λ*(3)

Diejenigen Werte, welche mit dem Modul $\lambda ^{*}(3)=\sin({\tfrac {1}{12}}\pi )$ in Verbindung stehen, werden Äquianharmonische Werte genannt:

$\theta _{c}{\bigl \{}{\tfrac {1}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}=2^{-1/6}3^{-7/12}(2+{\sqrt {3}})^{1/4}({\sqrt[{3}]{4}}-{\sqrt[{3}]{2}}+1)$

$\theta _{c}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}{\sqrt[{3}]{18}}\,(-{\sqrt[{3}]{4}}+{\sqrt {3}}+1)$

$\theta _{d}{\bigl \{}{\tfrac {1}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}\,{\sqrt[{3}]{9}}\,(2+{\sqrt {3}})^{-1/4}({\sqrt[{3}]{2}}+{\sqrt {3}}+1)$

$\theta _{d}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}{\sqrt[{3}]{18}}\,({\sqrt[{3}]{2}}+1)$

$\theta _{n}{\bigl \{}{\tfrac {1}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}=2^{-1/6}3^{-1/3}(2+{\sqrt {3}})^{-1/4}({\sqrt[{3}]{2}}+1)$

$\theta _{n}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}{\sqrt[{3}]{9}}\,({\sqrt {3}}-1)\,({\sqrt[{3}]{2}}+{\sqrt {3}}+1)$

Werte für Modul λ*(6)

Eingesetzt wird nun der Modulwert $\lambda ^{*}(6)=(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}})$ und dieser Wert für $w_{R5}$ ist der Schlüssel:

$w_{R5}{\bigl [}(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr ]}={\text{g}}(150)\div {\text{g}}(6)^{5}=\cot {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}$

So können direkt diese Neville-Theta-Werte hervorgebracht werden:

$\theta _{n}{\bigl \{}{\tfrac {2}{5}}K{\bigl [}(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr ]};(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr \}}=$

$=2^{-1/2}\cot {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/2}\tan {\bigl [}{\tfrac {1}{8}}\pi -{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/10}\cot {\bigl [}{\tfrac {1}{8}}\pi +{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{3/10}$

$\theta _{n}{\bigl \{}{\tfrac {4}{5}}K{\bigl [}(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr ]};(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr \}}=$

$=2^{-1/2}\cot {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/2}\cot {\bigl [}{\tfrac {1}{8}}\pi -{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/10}\tan {\bigl [}{\tfrac {1}{8}}\pi +{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{3/10}$

Theoreme der Nevilleschen Funktionen

Reflexive Theoreme als Grundlage

Während die Jacobischen Amplitudenfunktionen vollständige Additionstheoreme in sich aufweisen, besitzen die Nevilleschen Thetafunktionen nur reflexive Theoreme. Aber diese Theoreme können für die Ermittlung von Identitäten der Nevilleschen Thetafunktionen über reduzierte Webernsche Modulfunktionen verwendet werden. So lauten die exakten Reflexionstheoreme für die Nevilleschen Thetafunktionen $\theta _{d}$ und $\theta _{n}$ in Abhängigkeit vom elliptischen Modul:

$\theta _{d}(a+b;k)\,\theta _{d}(a-b;k)=(1-k^{2})\,\theta _{n}(a;k)^{2}\theta _{n}(b;k)^{2}+k^{2}\theta _{c}(a;k)^{2}\theta _{c}(b;k)^{2}$

$(1-k^{2})\,\theta _{n}(a+b;k)\,\theta _{n}(a-b;k)=\theta _{d}(a;k)^{2}\theta _{d}(b;k)^{2}-k^{2}\theta _{c}(a;k)^{2}\theta _{c}(b;k)^{2}$

Vervielfachungstheoreme

Aus den genannten reflexiven Theoremen und den Verdopplungstheoremen können die Verdreifachungstheoreme durch sukzessive Verkettungen erzeugt werden.

Dies sind einige Verdopplungstheoreme:

$\theta _{c}(2x;k)=\theta _{c}(x;k)^{4}\,\theta _{n}(x;k)^{2}-\,\theta _{d}(x;k)^{2}\,\theta _{s}(x;k)^{2}$

$\theta _{d}(2x;k)=(1-k^{2})\,\theta _{n}(x;k)^{4}+k^{2}\theta _{c}(x;k)^{4}$

$(1-k^{2})\,\theta _{n}(2x;k)=\theta _{d}(x;k)^{4}-k^{2}\theta _{c}(x;k)^{4}$

$\theta _{s}(2x;k)=2\,\theta _{c}(x;k)\theta _{d}(x;k)\theta _{n}(x;k)\theta _{s}(x;k)$

Die Thetawerte der doppelten Maßeinträge stehen zu den Thetawerten der einfachen Maßeinträge in einer glatt Quartischen Beziehung.

Auf der Grundlage der nun genannten Verdopplungstheoreme entstehen so die Verdreifachungstheoreme.

Durch den Einsatz von $a=2x$ und $b=x$ kommen diese Formeln direkt hervor:

$\theta _{d}(3x;k)\,\theta _{d}(x;k)=(1-k^{2})\,\theta _{n}(2x;k)^{2}\theta _{n}(x;k)^{2}+k^{2}\theta _{c}(2x;k)^{2}\theta _{c}(x;k)^{2}$

$(1-k^{2})\,\theta _{n}(3x;k)\,\theta _{n}(x;k)=\theta _{d}(2x;k)^{2}\theta _{d}(x;k)^{2}-k^{2}\theta _{c}(2x;k)^{2}\theta _{c}(x;k)^{2}$

Allgemeine Identitäten

Identitäten für die Drittelung von K

Jacobischer Rechenweg

Gegeben sind folgende Tangentielle Rechenoperatoren:

$a\oplus b=\tan {\bigl [}\arctan(a)+\arctan(b){\bigr ]}={\frac {a+b}{1-ab}}$

$c\ominus d=\tan {\bigl [}\arctan(c)-\arctan(d){\bigr ]}={\frac {c-d}{1+cd}}$

Als tangentielle Differenz kann direkt nach folgendem Schema der Sinus Amplitudinis vom Drittel des vollständigen elliptischen Integrals K ermittelt werden:

$\operatorname {sn} {\biggl \langle }{\frac {1}{3}}K{\biggl \{}\tan {\bigl [}{\frac {1}{2}}\arctan(t^{3}){\bigr ]}{\biggr \}};\tan {\bigl [}{\frac {1}{2}}\arctan(t^{3}){\bigr ]}{\biggr \rangle }={\bigl (}\,{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{2}+1}}\,{\bigr )}\ominus 1$

Aus diesem Wert können die anderen Werte einfach aufgebaut werden:

$\operatorname {cn} [{\tfrac {2}{3}}K(k);k]=1-\operatorname {sn} [{\tfrac {1}{3}}K(k);k]$

$\operatorname {dn} [{\tfrac {2}{3}}K(k);k]=\operatorname {cn} [{\tfrac {2}{3}}K(k);k]\div \operatorname {sn} [{\tfrac {1}{3}}K(k);k]$

$\operatorname {dn} [{\tfrac {1}{3}}K(k);k]={\sqrt {1-k^{2}}}\,\operatorname {sn} [{\tfrac {1}{3}}K(k);k]\div \operatorname {cn} [{\tfrac {2}{3}}K(k);k]$

Für die Drittelungen und Fünftelungen des vollständigen elliptischen Integrals K werden im nun Folgenden die Identitäten in Relation zu den Jacobischen Amplitudenfunktionen und zu den reduzierten Weberschen Modulfunktionen genannt:

Diese Formeln gelten für die Dreiteilung des vollständigen elliptischen Integrals erster Art K:

$\theta _{d}{\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{12}]{1-k^{2}}}{\sqrt[{3}]{4\operatorname {dn} [{\tfrac {1}{3}}K(k);k]\operatorname {nc} [{\tfrac {2}{3}}K(k);k]}}$

$\theta _{d}{\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{3}]{4\operatorname {ns} [{\tfrac {1}{3}}K(k);k]\operatorname {dn} [{\tfrac {2}{3}}K(k);k]}}$

Weberscher Rechenweg

Das sind die Theoreme für die Reduzierten Weberschen Modulfunktionen von der Stufe Drei:

${\color {ProcessBlue}w_{R3}(\varepsilon )^{12}-2{\sqrt {2}}\,w_{R3}(\varepsilon )^{9}-\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}{\bigl [}2{\sqrt {2}}\,w_{R3}(\varepsilon )^{3}+1{\bigr ]}=0}$

${\color {RoyalBlue}W_{R3}(\varepsilon )^{12}-2{\sqrt {2}}\,W_{R3}(\varepsilon )^{9}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}{\bigl [}2{\sqrt {2}}\,W_{R3}(\varepsilon )^{3}+1{\bigr ]}=0}$

Neben den genannten Theoremen kann auch eine Parametrisierungsformel für die Ermittlung der reduzierten Weberschen Modulfunktionen herangezogen werden:

$w_{R3}{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}=2^{-1/6}\left({\sqrt {t^{2}+1}}\,{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{4}-t^{2}+1}}+1\right)^{1/3}$

Mit den reduzierten Weberschen Modulfunktionen gilt:

$\theta _{n}{\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt {2}}\,w_{R3}(k)$

$\theta _{d}{\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt {2}}\,W_{R3}(k)$

Mit den Ramanujanschen Funktionen ${\text{g}}$ und ${\text{G}}$ sowie mit der Elliptischen Lambda-Stern-Funktion gelten diese Beziehungen:

$\theta _{n}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\lambda ^{*}(m){\bigr ]};\lambda ^{*}(m){\bigr \}}={\tfrac {1}{2}}{\sqrt {2}}\,{\text{g}}(m)^{-3}{\text{g}}(9\,m)$

$\theta _{d}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\lambda ^{*}(m){\bigr ]};\lambda ^{*}(m){\bigr \}}={\tfrac {1}{2}}{\sqrt {2}}\,{\text{G}}(m)^{-3}{\text{G}}(9\,m)$

Identitäten für die Fünftelung von K

Reduzierte Webersche Modulfunktionen

Die Reduzierten Weberschen Funktionen $w_{R5}(k)$ und $W_{R5}(k)$ dienen zur schnellen sowie effizienten Ermittlung der Nevilleschen Thetafunktionswerte von den Fünfteln des K-Integrals:

Die Definitionen und Identitäten dieser beiden Funktionen sind in nachfolgender Tabelle zusammengefasst:

Definitionen und Identitäten von w und W

Kleine reduzierte Webersche Funktion	Große reduzierte Webersche Funktion
Pochhammersche Definitionen
${\color {ProcessBlue}w_{R5}(k)={\frac {2\,[q(k)^{5};q(k)^{10}]_{\infty }}{[q(k);q(k)^{2}]_{\infty }^{5}}}}$	${\color {RoyalBlue}W_{R5}(k)={\frac {2\,[q(k)^{10};q(k)^{20}]_{\infty }\,[q(k);q(k)^{2}]_{\infty }^{5}}{[q(k)^{5};q(k)^{10}]_{\infty }\,[q(k)^{2};q(k)^{4}]_{\infty }^{5}}}}$
Ramanujansche Definitionen
${\color {ProcessBlue}w_{R5}(\varepsilon )={\frac {{\text{g}}[25K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]}{{\text{g}}[K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]^{5}}}}$	${\color {RoyalBlue}W_{R5}(\varepsilon )={\frac {{\text{G}}[25K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]}{{\text{G}}[K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]^{5}}}}$
Jacobische Thetaformeln
${\color {ProcessBlue}w_{R5}(k)={\frac {5\,\vartheta _{01}[q(k)^{5}]^{2}}{2\,\vartheta _{01}[q(k)]^{2}}}-{\frac {1}{2}}}$	${\color {RoyalBlue}W_{R5}(k)={\frac {5\,\vartheta _{00}[q(k)^{5}]^{2}}{2\,\vartheta _{00}[q(k)]^{2}}}-{\frac {1}{2}}}$
Bilanzen der Amplitudenfunktionen
${\color {ProcessBlue}w_{R5}(k)=\operatorname {nc} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}-\operatorname {nc} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}}$	${\color {RoyalBlue}W_{R5}(k)=\operatorname {dn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}+\operatorname {dn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}}$

Die Funktionen ${\text{g}}$ und ${\text{G}}$ stellen die Ramanujanschen Funktionen dar.

Mit Gleichungen sechsten Grades ermittelt man die Werte der genannten Reduzierten Weberschen Modulfunktionen in Abhängigkeit vom Modul k simultan oder sukzessiv:

${\color {ProcessBlue}w_{R5}(k)^{6}-2\,w_{R5}(k)^{5}}=\tan {\bigl [}2\arctan(k){\bigr ]}^{2}{\color {ProcessBlue}{\bigl [}2\,w_{R5}(k)+1{\bigr ]}}$

${\color {RoyalBlue}2\,W_{R5}(k)^{5}-W_{R5}(k)^{6}}=\sin {\bigl [}2\arcsin(k){\bigr ]}^{2}{\color {RoyalBlue}{\bigl [}2\,W_{R5}(k)+1{\bigr ]}}$

Dieselben Gleichungen können auch weiter vereinfacht über die Tangensdifferenz mit der Zahl Zwei dargestellt werden:

$w_{R5}(k)\ominus 2=\tan {\bigl [}2\arctan(k){\bigr ]}^{2}w_{R5}(k)^{-5}$

$2\ominus W_{R5}(k)=\sin {\bigl [}2\arcsin(k){\bigr ]}^{2}W_{R5}(k)^{-5}$

Von der Funktion $w_{R5}$ auf die Funktion $W_{R5}$ kann so übergeleitet werden:

$W_{R5}(k)=w_{R5}(k)^{-2}{\biggl \{}{\frac {1-k^{2}}{1+k^{2}}}{\bigl [}w_{R5}(k)^{2}-w_{R5}(k)-1{\bigr ]}{\bigl [}w_{R5}(k)^{2}+1{\bigr ]}+w_{R5}(k)+1{\biggr \}}$

Direkt daraus können im Anschluss die Nevilleschen Thetafunktionswerte so ermittelt werden:

$\theta _{n}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}=2^{-1/2}\,w_{R5}(k)^{1/2}\tan {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\cot {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{3/10}$

$\theta _{n}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}=2^{-1/2}\,w_{R5}(k)^{1/2}\cot {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{3/10}$

Die andere von den beiden reduzierten Weberschen Modulfunktionen liefert diese Resultate auf einfache Weise:

$\theta _{d}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}=2^{-1/2}\,W_{R5}(k)^{1/2}\tan {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\cot {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{3/10}$

$\theta _{d}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}=2^{-1/2}\,W_{R5}(k)^{1/2}\cot {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{3/10}$

Folgende weitere Beziehungen führen zu den Neville-Theta-Werten aus einem Fünftel und drei Fünfteln vom Integral K:

$\theta _{d}{\bigl [}{\tfrac {1}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}\,\theta _{n}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}$

$\theta _{d}{\bigl [}{\tfrac {3}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}\,\theta _{n}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}$

Jacobische Schlüsselwerte

Die folgenden Tangensdifferenzen gereichen zur Ermittlung der Amplitudenfunktionswerte:

$\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {2\,W_{R5}(\varepsilon )+1}}{\bigl [}{\sqrt {W_{R5}(\varepsilon )^{2}+1}}+W_{R5}(\varepsilon ){\bigr ]}\ominus 1$

$\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}=1\ominus {\sqrt {2\,W_{R5}(\varepsilon )+1}}{\bigl [}{\sqrt {W_{R5}(\varepsilon )^{2}+1}}-W_{R5}(\varepsilon ){\bigr ]}$

Eine weitere Fortpflanzung der Amplitudenfunktionswerte erfolgt dadurch:

$\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}$

$\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}$

$\operatorname {dn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-k^{2}+k^{2}\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}$

$\operatorname {dn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-k^{2}+k^{2}\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}$

Durch Zuhilfenahme der Jacobischen Amplitudenfunktionswerte lassen sich die Nevilleschen Werte ebenso ermitteln:

$\theta _{d}{\bigl [}{\tfrac {1}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {nd} [{\tfrac {4}{5}}K(k);k]}}$

$\theta _{d}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {dn} [{\tfrac {2}{5}}K(k);k]^{4}}}$

$\theta _{d}{\bigl [}{\tfrac {3}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {nd} [{\tfrac {2}{5}}K(k);k]}}$

$\theta _{d}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {dn} [{\tfrac {4}{5}}K(k);k]^{4}}}$

Identitäten für die Siebenteilung von K

Für die Siebenteilung gelten diese Identitäten der Nevilleschen Thetaprodukte:

$\theta _{n}{\bigl [}{\tfrac {2}{7}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {4}{7}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {6}{7}}K(k);k{\bigr ]}=2^{-3/2}w_{R7}(k)$

$\theta _{d}{\bigl [}{\tfrac {2}{7}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {4}{7}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {6}{7}}K(k);k{\bigr ]}=2^{-3/2}W_{R7}(k)$

Die Produkte der Werte $\theta _{n}$ und auch die Produkte der Werte $\theta _{d}$ ergeben stets die Werte w beziehungsweise W der reduzierten Weberschen Modulfunktionen:

$w_{R7}(k)={\frac {{\text{g}}[49K'(k)^{2}\div K(k)^{2}]}{{\text{g}}[K'(k)^{2}\div K(k)^{2}]^{7}}}$

$W_{R7}(k)={\frac {{\text{G}}[49K'(k)^{2}\div K(k)^{2}]}{{\text{G}}[K'(k)^{2}\div K(k)^{2}]^{7}}}$

Die reduzierten Weberschen Funktionen der Stufe Sieben werden durch Gleichungen achten Grades gelöst:

${\color {ProcessBlue}w_{R7}(\varepsilon )^{8}-2{\sqrt {2}}\,w_{R7}(\varepsilon )^{7}-7\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}w_{R7}(\varepsilon )^{4}+\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{4}{\bigl [}-2{\sqrt {2}}\,w_{R7}(\varepsilon )+1{\bigr ]}=0}$

${\color {RoyalBlue}W_{R7}(\varepsilon )^{8}-2{\sqrt {2}}\,W_{R7}(\varepsilon )^{7}+7\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}W_{R7}(\varepsilon )^{4}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{4}{\bigl [}-2{\sqrt {2}}\,W_{R7}(\varepsilon )+1{\bigr ]}=0}$

Identitäten für die Elfteilung von K

Für die Elfteilung gelten diese Identitäten der Nevilleschen Thetaprodukte:

$\theta _{n}{\bigl [}{\tfrac {2}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {4}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {6}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {8}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {10}{11}}K(k);k{\bigr ]}=2^{-5/2}w_{R11}(k)$

$\theta _{d}{\bigl [}{\tfrac {2}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {4}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {6}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {8}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {10}{11}}K(k);k{\bigr ]}=2^{-5/2}W_{R11}(k)$

Analog zum vorherigen Fall gilt auch für diesen Fall das folgende Muster:

$w_{R11}(k)={\frac {{\text{g}}[121K'(k)^{2}\div K(k)^{2}]}{{\text{g}}[K'(k)^{2}\div K(k)^{2}]^{11}}}$

$W_{R11}(k)={\frac {{\text{G}}[121K'(k)^{2}\div K(k)^{2}]}{{\text{G}}[K'(k)^{2}\div K(k)^{2}]^{11}}}$

Die reduzierten Weberschen Funktionen der Stufe Elf werden durch Gleichungen zwölften Grades gelöst:

${\color {ProcessBlue}w_{R11}(\varepsilon )^{12}-\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{10}=2{\sqrt {2}}\,w_{R11}(\varepsilon ){\bigl \{}w_{R11}(\varepsilon )^{2}+\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}{\bigr \}}\times }$

${\color {ProcessBlue}\times {\bigl \{}w_{R11}(\varepsilon )^{4}+3\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}w_{R11}(\varepsilon )^{2}+\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{4}{\bigr \}}\times }$

${\color {ProcessBlue}\times {\bigl \{}2\,w_{R11}(\varepsilon )^{4}+3\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}w_{R11}(\varepsilon )^{2}+2\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{4}{\bigr \}}}$

${\color {RoyalBlue}W_{R11}(\varepsilon )^{12}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{10}=2{\sqrt {2}}\,W_{R11}(\varepsilon ){\bigl \{}W_{R11}(\varepsilon )^{2}-\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}{\bigr \}}\times }$

${\color {RoyalBlue}\times {\bigl \{}W_{R11}(\varepsilon )^{4}-3\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}W_{R11}(\varepsilon )^{2}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{4}{\bigr \}}\times }$

${\color {RoyalBlue}\times {\bigl \{}2\,W_{R11}(\varepsilon )^{4}-3\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}W_{R11}(\varepsilon )^{2}+2\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{4}{\bigr \}}}$

Genau dann, wenn der Webersche Funktionsindex in Form einer ungerade Zahl größer als Eins eine Primzahl ist, hat die korrespondierende Gleichung mit dem reduzierten Weberschen Funktionswert als Lösung der Gleichung einen Grad gleich dem Nachfolger des Funktionsindex.

Jacobische Amplitudenfunktionen

Allgemein gültige Regel

Alle Jacobischen Amplituenfunktionen können nach folgendem Schema direkt erzeugt werden:

$\operatorname {pq} (u;k)={\frac {\theta _{p}(u;k)}{\theta _{q}(u;k)}}$

Hierbei stehen die Buchstaben $p$ und $q$ stellvertretend für die Buchstaben $c$, $d$, $n$ und $s$ und so dient diese Formel für die Erstellung der gesamten Gruppe aller Jacobischen Elliptischen Funktionen der Standard-Amplitudenform!

Beispielsweise gelten für den Sinus Amplitudinis und seine um das K-Integral horizontal verschobene Funktion folgende Quotienten:

$\operatorname {sn} (u;k)={\frac {\theta _{s}(u;k)}{\theta _{n}(u;k)}}$

$\operatorname {cd} (u;k)={\frac {\theta _{c}(u;k)}{\theta _{d}(u;k)}}$

Additionstheoreme

Während die Nevilleschen Thetafunktionen nur Reflexionstheoreme in sich aufweisen, besitzen die sich als Quotienten der Nevilleschen Funktionen ergebenden Jacobischen Amplitudenfunktionen sogar vollständige Additionstheoreme:

$\operatorname {sn} (x+y;k)={\frac {\operatorname {sn} (x;k)\operatorname {cd} (y;k)+\operatorname {cd} (x;k)\operatorname {sn} (y;k)}{1+k^{2}\operatorname {sn} (x;k)\operatorname {cd} (x;k)\operatorname {sn} (y;k)\operatorname {cd} (y;k)}}$

$\operatorname {cd} (x+y;k)={\frac {\operatorname {cd} (x;k)\operatorname {cd} (y;k)-\operatorname {sn} (x;k)\operatorname {sn} (y;k)}{1-k^{2}\operatorname {sn} (x;k)\operatorname {cd} (x;k)\operatorname {sn} (y;k)\operatorname {cd} (y;k)}}$

Ableitungen

Definition des Zeta Amplitudinis

Die Ableitungen der Nevilleschen Thetafunktionen lassen sich vereinfacht mit Hilfe der Jacobischen Zetafunktion $\mathrm {zn}$ darstellen.

Das Zeta Ampitudinis ist so definiert:

${\text{zn}}(z;k)=E[{\text{am}}(z;k);k]-{\frac {E(k)z}{K(k)}}$

${\text{zn}}(z;k)=\sum _{n=1}^{\infty }{\frac {4\sin {\bigl [}2\,z\div {\bar {K}}(k){\bigr ]}q(k)^{2n-1}}{{\bar {K}}(k){\bigl \{}1-2\cos {\bigl [}2\,z\div {\bar {K}}(k){\bigr ]}q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}}}$

Erstableitungsliste

So werden die ersten Ableitungen beziehungsweise Differentialquotienten ermittelt:

${\frac {\partial }{\partial \,x}}\,\theta _{n}(x;k)=\theta _{n}(x;k)\,\mathrm {zn} (x;k)$

${\frac {\partial }{\partial \,x}}\,\theta _{d}(x;k)=\theta _{d}(x;k){\bigl [}\mathrm {zn} (x;k)-k^{2}\mathrm {sn} (x;k)\,\mathrm {cd} (x;k){\bigr ]}$

${\frac {\partial }{\partial \,x}}\,\theta _{c}(x;k)=\theta _{c}(x;k){\bigl [}\mathrm {zn} (x;k)-\mathrm {sn} (x;k)\,\mathrm {dc} (x;k){\bigr ]}$

Begründung der Produktformel für Neville-Theta-n

Die gerade eben genannte Formel kann auch als sogenannte Logarithmische Ableitung dargestellt werden:

${\frac {\partial }{\partial \,x}}\ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\mathrm {zn} (x;k)$

Das war die zuvor erwähnte Formel für das Zeta Amplitudinis:

$\mathrm {zn} (x;k)=\sum _{n=1}^{\infty }{\frac {4\sin[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}}{{\bar {K}}(k){\bigl \{}1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}}}$

Mit dem Einsetzungsverfahren kommt diese Formel hervor:

${\frac {\partial }{\partial \,x}}\ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\sum _{n=1}^{\infty }{\frac {4\sin[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}}{{\bar {K}}(k){\bigl \{}1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}}}$

Auf den Logarithmus Naturalis von der Nevilleschen Theta-n-Funktion gelangt man somit durch Bildung der Ursprungsstammfunktion bezüglich x:

$\ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\sum _{n=1}^{\infty }{\biggl \langle }\ln {\bigl \{}1-2\cos {\bigl [}2\,x\div {\bar {K}}(k){\bigr ]}q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}-2\ln {\bigl [}1-q(k)^{2n-1}{\bigr ]}{\biggr \rangle }$

$\ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\sum _{n=1}^{\infty }\,\ln {\biggl \{}{\frac {1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{[1-q(k)^{2n-1}]^{2}}}{\biggr \}}$

Der nun genannte Ausdruck wird nun der Exponentialfunktion als äußere Funktion anvertraut:

$\theta _{n}(x;k)=\exp {\biggl \langle }\sum _{n=1}^{\infty }\,\ln {\biggl \{}{\frac {1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{[1-q(k)^{2n-1}]^{2}}}{\biggr \}}{\biggr \rangle }$

Der Exponentialfunktionswert aus der Summe ist gleich dem Produkt der Exponentialfunktionswerte:

$\theta _{n}(x;k)=\prod _{n=1}^{\infty }{\frac {1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{[1-q(k)^{2n-1}]^{2}}}$

QUOD ERAT DEMONSTRANDUM

Zweitableitungsliste

So werden dementsprechend die zweiten Ableitungen ermittelt:

${\frac {\partial ^{2}}{\partial \,x^{2}}}\,\theta _{n}(x;k)=\theta _{n}(x;k){\bigl [}\mathrm {zn} (x;k)^{2}+\mathrm {dn} (x;k)^{2}-E(k)\div K(k){\bigr ]}$

${\frac {\partial ^{2}}{\partial \,x^{2}}}\,\theta _{d}(x;k)=\theta _{d}(x;k){\bigl \{}{\bigl [}\mathrm {zn} (x;k)-k^{2}\mathrm {sn} (x;k)\,\mathrm {cd} (x;k){\bigr ]}^{2}+(1-k^{2})\,\mathrm {nd} (x;k)^{2}-E(k)\div K(k){\bigr \}}$

${\frac {\partial ^{2}}{\partial \,x^{2}}}\,\theta _{c}(x;k)=\theta _{c}(x;k){\bigl \{}{\bigl [}\mathrm {zn} (x;k)-\mathrm {sn} (x;k)\,\mathrm {dc} (x;k){\bigr ]}^{2}-(1-k^{2})\,\mathrm {sc} (x;k)^{2}-E(k)\div K(k){\bigr \}}$

Integrale

Die bestimmten Integrale von Null bis zum K-Wert ergeben folgende Resultate:

$\int _{0}^{K(k)}\theta _{d}(x;k)\,\mathrm {d} x={\biggl [}{\frac {\pi }{2}}\,K(k){\biggr ]}^{1/2}={\frac {\pi }{2}}\,{\bar {K}}(k)^{1/2}$

$\int _{0}^{K(k)}\theta _{n}(x;k)\,\mathrm {d} x={\biggl [}{\frac {\pi }{2k'}}\,K(k){\biggr ]}^{1/2}={\frac {\pi }{2}}(1-k^{2})^{-1/4}\,{\bar {K}}(k)^{1/2}$

Symmetriebeziehungen

• $\theta _{c}(z;k)=\theta _{c}(-z;k)$
• $\theta _{d}(z;k)=\theta _{d}(-z;k)$
• $\theta _{n}(z;k)=\theta _{n}(-z;k)$
• $\theta _{s}(z;K)=-\theta _{s}(-z;k)$

Komplexe 3D-Schemata

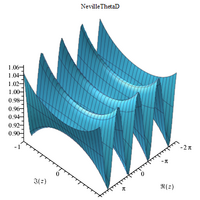
Die nun folgenden 3D-Schemata stellen den reellen Anteil und den imaginären Anteil der Nevilleschen Thetafunktionen zueinander gegenüber:

Implementationen

NetvilleThetaC[z,m], NevilleThetaD[z,m], NevilleThetaN[z,m], and NevilleThetaS[z,m] sind hierbei die eingebaute Funktionen von Wolfram Mathematica und der rechte Klammerabschnitt enthält das Quadrat der numerischen Exzentrizität $m=k^{2}$ beziehungsweise das Quadrat des Moduls bei den Wolfram-Eingabebefehlen.

Anwendungen

Die allgemeine Summenreihe aus Potenzen als Summanden mit konstanter Basis bezüglich des Summenindex und Exponenten in quadratischer Relation zum Summenindex lässt sich generell auf folgende Weise berechnen:

$\sum _{n=-\infty }^{\infty }Q^{(n+R)^{2}}={\frac {\vartheta _{00}(Q)}{\vartheta _{00}(Q')}}\,\vartheta _{00}{\bigl (}\pi \,R\,;Q'{\bigr )}=\vartheta _{00}(Q)\,\theta _{d}{\bigl \{}2\,R\,K{\bigl [}\psi _{H}(Q)^{4}{\bigr ]};\psi _{H}(Q)^{4}{\bigr \}}$

$Q'=\exp {\bigl [}\pi ^{2}\div \ln(Q){\bigr ]}$

Dabei stellt das Kürzel $\psi _{H}$ die Hermitesche elliptische Psifunktion dar:

$\psi _{H}(w)=\vartheta _{01}(w)^{1/2}\vartheta _{00}(w)^{-1/2}$

$\psi _{H}(w)=\vartheta _{01}(w)\,\vartheta _{01}(w^{2})^{-1}$

Für den Nevilleschen Ausdruck werden im Folgenden zwei Beispiele angeführt:

$\sum _{n=-\infty }^{\infty }{\bigl (}{\frac {1}{2}}{\bigr )}^{(n+1/3)^{2}}=\vartheta _{00}{\bigl (}{\frac {1}{2}}{\bigr )}\theta _{d}{\bigl \{}{\frac {2}{3}}K{\bigl [}\psi _{H}{\bigl (}{\frac {1}{2}}{\bigr )}^{4}{\bigr ]};\psi _{H}{\bigl (}{\frac {1}{2}}{\bigr )}^{4}{\bigr \}}$

$\sum _{n=-\infty }^{\infty }{\bigl (}{\frac {2}{3}}{\bigr )}^{(n+2/5)^{2}}=\vartheta _{00}{\bigl (}{\frac {2}{3}}{\bigr )}\theta _{d}{\bigl \{}{\frac {4}{5}}K{\bigl [}\psi _{H}{\bigl (}{\frac {2}{3}}{\bigr )}^{4}{\bigr ]};\psi _{H}{\bigl (}{\frac {2}{3}}{\bigr )}^{4}{\bigr \}}$

Literatur

• E. H. (Eric Harold) Neville: Jacobian Elliptic Functions. Oxford Clarendon Press, 1944 (archive.org). 
• Eric W. Weisstein: Neville Theta Functions. In: MathWorld (englisch).