Newtongerade
Zur Navigation springen
Zur Suche springen
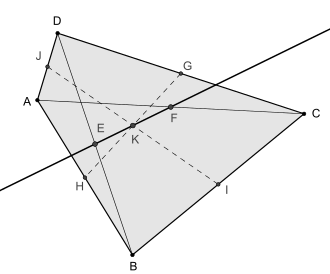
Als Newtongerade bezeichnet man die Gerade, die in einem konvexen Viereck, das kein Parallelogramm ist, durch die Mittelpunkte der beiden Diagonalen verläuft. Parallelogramme müssen in dieser Definition ausgenommen werden, da die Mittelpunkte der Diagonalen bei Parallelogrammen zusammenfallen und daher keine Gerade definieren.
Die beiden Strecken, die in einem konvexen Viereck die Mittelpunkte gegenüberliegender Seiten verbinden, schneiden sich in einem Punkt, der auf der Newtongeraden liegt. Ist das konvexe Viereck darüber hinaus auch ein Tangentenviereck, so liegt nach dem Satz von Newton der Mittelpunkt des Inkreises ebenfalls auf der Newtongeraden.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, S. 108–109, 116–118 (Auszug (Google))
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Alexander Bogomolny: Bimedians in a Quadrilateral auf cut-the-knot.org