Nussinov-Algorithmus
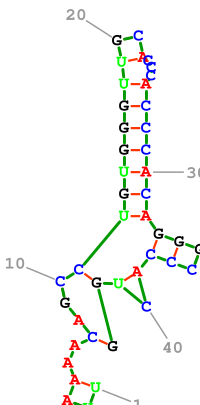
Der Nussinov-Algorithmus ist ein einfacher Algorithmus zur Berechnung der maximal möglichen Anzahl von Basenpaaren in einer RNA-Sequenz und einer oder mehrerer möglicher Sekundärstrukturen dieser RNA-Sequenz. Wegen seiner einfachen Modell-Annahmen ist seine biologische Bedeutung gering, er wird aber in der Didaktik der Bioinformatik als einfaches Beispiel für dynamische Programmierung verwendet und dient als Ausgangspunkt für komplexere Modelle.
Algorithmus
[Bearbeiten | Quelltext bearbeiten]Modell
[Bearbeiten | Quelltext bearbeiten]Der Algorithmus modelliert eine RNA-Sequenz und die Basenpaare innerhalb dieser Sequenz als einen planaren Graphen, das heißt ohne Pseudoknoten. Zwischen den Basen eines einzigen Basenpaares liegt mindestens eine weitere Base, d. h., die Schleife einer Haarnadelstruktur besteht aus mindestens einer Base.
Gegeben ist die Sequenz der einzelnen Basen als eine Zeichenkette mit der Länge . Dabei bezeichnet das Zeichen an der Stelle und die Teil-Sequenz der Zeichen von der Stelle bis zur Stelle . Damit ist gleichbedeutend mit und ist . Weiters sei eine leere Zeichenkette der Länge 0.
![{\displaystyle s[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95c8024dbbc210b378cf497974e51129a7bd62b4)
![{\displaystyle s[i..j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebf63bf22305c7594ef2b27c8e639491a86fe7ac)
![{\displaystyle s[i..i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cd601bd829a5d3147fa981e98d4f81459652b99)
![{\displaystyle s[1..n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1d6d75312c0130675dda344d2eecb69cf8e12be)
![{\displaystyle s[i..i-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9de5ba85ca4bee6116e037e11568961ee300065a)
Die Matrix der Größe enthält die die Anzahl der maximal möglichen Basenpaare der Teilsequenzen für der Sequenz . Das Matrixelement bezeichnet dementsprechend die Anzahl der maximal möglichen Basenpaare für die gesamte Sequenz.
![{\displaystyle N[i,j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfc3f50a38385d9c65e6a67e9be3cf3989c1be00)
![{\displaystyle N[1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/493db03d387e62a2bec2d67f6e1ad74491ced2ed)
Die Funktion ergibt 1, wenn und komplementäre Basen sind, sonst 0.
![{\displaystyle s[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60c5252fdedb32516342487b03fbf6654c12a1f1)
Pseudoknoten sind im Modell nicht erlaubt, d. h., für zwei Basenpaare und gilt oder
![{\displaystyle (s[a];s[b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e57b4fb429e86be688662b208c8307635d5b5ed7)
![{\displaystyle (s[c];s[d])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d9be87b7a98ac42b9182d42a12accd2a721bf7f)
Zerlegung in kleinere Teil-Probleme
[Bearbeiten | Quelltext bearbeiten]Die Elemente der Matrix werden berechnet, indem zuerst angenommen wird, alle Elemente bis auf das Element , das die Sequenz beschreibt, seien bekannt. Die Sequenz kann gebildet werden, indem der Sequenz die Base angehängt wird. Diese Base kann nun entweder mit einem anderen Element der Sequenz ein Basenpaar bilden oder nicht:
![{\displaystyle s[1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33860e142f40f3a925655ee6311439003a01f763)
![{\displaystyle s[1,n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfde566a3a809a552d156ae1df880d676e673481)
![{\displaystyle s[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe878c033cc70d1aa3ffbd156394791aa8dffde)
- Falls kein Basenpaar gebildet wird, so muss sein und das Problem ist gelöst.
- Falls ein Basenpaar gebildet wird, so kann dieses Basenpaar zwischen und einer der Basen aus der Teil-Sequenz gebildet werden. Angenommen, das Basenpaar bildet sich zwischen und mit so teilt sich die Sequenz in die weiteren Teile und . Für diese beiden Teile kann wiederum die Anzahl der maximal möglichen Basenpaare berechnet werden, indem der Algorithmus für diese Teile von Neuem begonnen wird. Die Summe der beiden Teile plus dem zwischen und gebildete Basenpaar ergibt einen möglichen Kandidaten-Wert für die Maximale Summe. Der Wert für soll maximal werden, also muss für jedes erlaubte die Kandidaten berechnet werden. Der höchste so erreichbare Wert garantiert, dass auch maximal wird. Somit ist
![{\displaystyle N[1,n]=N[1,n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ae039054191c356613c1f294d2c977930e47e95)
![{\displaystyle s[1..n-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fc0002712c0ee30613231f023b8799b17a715c9)
![{\displaystyle s[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db206b1becb7d7eadf223e75c8626dd9bfc1dbdd)
![{\displaystyle s[1..k-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a7c75374fd8c75212b5679a9288968f9fdf7511)
![{\displaystyle s[k+1..n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c712a08c09301bfc788c6b9ccb8aeb3f78174c0)
![{\displaystyle N[1,n]=\max {\begin{Bmatrix}\max _{1<k<n-1}(N[1,k-1]+N[k+1,n-1]+1)\cdot \sigma (k,n)&\\N[2,n-1]\cdot \sigma (1,n)&\end{Bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec96fc7508618982b7b1c3e8941e12fb69d9e6fd)
und das Problem ist ebenfalls gelöst. Der untere Term der Maximalwertsberechnung behandelt den Sonderfall eines Basenpaares zwischen dem ersten und dem letzten Element der Sequenz, wodurch eine der Teilsequenzen leer ist (). Beide gelisteten Möglichkeiten werden überprüft und die höhere so erreichbare Anzahl an Basenpaaren ist das Ergebnis der Berechnung.
![{\displaystyle s[0,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdb89bc7614e62b27a3816511b98085e56a74a47)
Der Algorithmus verkleinert die Sequenz auf diese Weise in immer kleinere Teil-Sequenzen, bis diese sofort berechnet werden können. Die Zwischenergebnisse werden dann zur Berechnung der nächstgrößeren Teil-Sequenzen verwendet.
Initialisierung
[Bearbeiten | Quelltext bearbeiten]Die Teil-Sequenzen der Länge 2, der Länge 1 und der Länge 0 enthalten maximal 0 Basenpaare:
![{\displaystyle s[i,i+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39db6a7cdaf31bac04262262fe9975530c09a57a)
![{\displaystyle s[i,i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40fa5c9ba2c9820f5f86408afa341280ce0ac43f)
![{\displaystyle s[i,i-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cca88b4935be39fb12dfd980549f93bff8e37f2e)
- für
![{\displaystyle N[i,i+1]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f506d711835487bf30d119e07af8ef33e28e4f9)
- für
![{\displaystyle N[i,i]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ba4b47584f3c1cc1ca7945d71b762316448fccc)
- für
![{\displaystyle N[i,i-1]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abbab482f8cd16e744a8823ffe947b7fea4838ee)
Rekursion
[Bearbeiten | Quelltext bearbeiten]Für die weiteren Elemente der Matrix gilt, unter der Voraussetzung, dass :
![{\displaystyle N[i,0]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/609fc3004013233a81d8a5343931954d490baa90)
- mit
![{\displaystyle N[i,j]=\max {\begin{Bmatrix}N[i,j-1]&\\\max _{i\leq k<j-1}(N[i,k-1]+N[k+1,j-1]+1)\cdot \sigma (k,j))&\end{Bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce21ae75df875e13823e2751681d863d4106cc13)
Das Element der Matrix ist nach Beendigung des Algorithmus die maximal mögliche Anzahl von Basenpaaren des Substrings von . Also ist die maximal mögliche Anzahl von Basenpaaren der gesamten Eingabesequenz in gespeichert.
![{\displaystyle N[1,n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/825ebe23994a555d6fd88d05ba4c0ed379e454f3)
Die Fallunterscheidung in der Rekursion unterscheidet zwei Fälle. Entweder wird der Substring , für den schon die maximal mögliche Anzahl von Basenpaaren schon berechnet wurde, um eine Base erweitert, welche nicht mit einer anderen Base paart. Oder die Base paart mit einer komplementären Base im Substring . Im zweiten Fall existieren mögliche Basen, mit denen ein Basenpaar bilden könnte. Die Wahl der zu komplementären Base teilt den Substring in zwei Substrings und , für die die maximale mögliche Anzahl von Basenpaaren rekursiv berechnet wird. Die Funktion hat den Wert , wenn die Base komplementär zu ist, ansonsten .
![{\displaystyle s[i..j-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f488f7014aed9445de619d278b8b4aaf25b55787)
![{\displaystyle s[i..k-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa93498e0569dca7999870faf9aad33caaf4cc39)
![{\displaystyle s[k+1..j-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d676905e1c495c7e71c5e52150dfb179bb64901)
Die Fallunterscheidung entspricht der kontextfreien Grammatik
wobei ein eine ungepaarte Base bezeichnet und die Klammern Platzhalter für alle möglichen komplementären Basenpaare darstellen. Nach dieser Grammatik können alle Strukturen, über die der Nussinov-Algorithmus optimiert, abgeleitet werden.
Die Sekundärstrukturen, welche die maximalen Basenpaare enthalten, können durch Backtracking von der Zelle erzeugt werden. Das heißt, es werden die Pfade durch die Matrix zurückverfolgt, die zu dem optimalen Ergebnis in führen und in Abhängigkeit dieser Pfade werden die optimalen Sekundärstrukturen erzeugt.
![{\displaystyle N[0,n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90dfe6f7715071271f485a9848f963aee3b21a59)
![{\displaystyle N[i,n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b1ec950237ecd8a630755faa6a868966ea3ac9d)
Effizienz
[Bearbeiten | Quelltext bearbeiten]Der Algorithmus verwendet eine Matrix mit Einträgen, für jeden Eintrag wird über Elemente optimiert. Der Speicherbedarf liegt also in der Komplexitätsklasse und die Laufzeit in .
Abgrenzung
[Bearbeiten | Quelltext bearbeiten]Die obige Spezifikation der Matrix-Rekurrenzen entspricht der Darstellung in Nussinov, 1978. Teilweise bezeichnet neuere Literatur eine Abwandlung dieser Rekurrenzen als Nussinov-Algorithmus (z. B. Durbin, 2006). In Durbin, 2006 besteht die Rekursion aus einer Unterscheidung von 4 Fällen. Diese Variation ändert nicht die Werte der berechneten Matrix , allerdings repräsentieren dann mehrere unterschiedliche Pfade beim Backtracking eine Sekundärstruktur, da die geänderte Fallunterscheidung semantisch mehrdeutig ist.
Biologische Relevanz
[Bearbeiten | Quelltext bearbeiten]Die Sekundärstruktur, welche die maximale Anzahl von Basenpaaren enthält ist nicht unbedingt die Struktur, die in der Natur (in einer Zelle) auftritt. Ebenso treten in natürlichen RNA-Faltmustern sehr wohl Pseudoknoten auf, die vom Nussinov-Algorithmus von vornherein nicht beachtet werden. In der Praxis wird daher die Sekundärstruktur anders, beispielsweise mit dem Zuker-Algorithmus mit thermodynamischem Modell, vorhergesagt, was zu biologisch sinnvolleren Ergebnissen führt.
Trotzdem ist der Nussinov-Algorithmus von theoretischem Interesse in Forschung und Lehre. Beispielsweise wird in[1] der Algorithmus verwendet, um die Waterman-Byers-Backtracking-Methode zum Backtracking von suboptimalen Strukturen exemplarisch an einer übersichtlichen Matrix-Rekursion zu beschreiben. Die Beschäftigung mit dem Algorithmus ist lehrreich, da er wie andere RNA-Strukturvorhersage-Algorithmen die Methode der dynamischen Programmierung verwendet, aber mit einer Matrix-Rekursion noch relativ einfach verständlich ist.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Ruth Nussinov, George Pieczenik, Jerrold R. Griggs, Daniel J. Kleitman: Algorithms for Loop Matchings. In: SIAM Journal on Applied Mathematics. Band 35, Nr. 1, Juli 1978, S. 68–82.
- Durbin et al.: Biological sequence analysis. Cambridge, 2006, ISBN 0-521-62971-3, S. 269–272.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Stefan Wuchty, Walter Fontana, Ivo L. Hofacker, Peter Schuster: Complete Suboptimal Folding of RNA and the Stability of Secondary Structures. In: Biopolymers. Band 49, 1999, S. 145–165 (santafe.edu [PDF; 317 kB]).