Gestörte Gamma-Gamma-Winkelkorrelation

PAC-Spektroskpie: Sonde im Wirtsgitter

Schema der PAC-Spektroskopie

Die gestörte γ-γ-Winkelkorrelation, kurz PAC (englisch perturbed angular correlation) oder PAC-Spektroskopie, ist eine Methode der nuklearen Festkörperphysik, mit der magnetische und elektrische Felder in Kristallstrukturen gemessen werden können. Dabei werden elektrische Feldgradienten und die Larmorfrequenz in Magnetfeldern sowie dynamische Effekte bestimmt. Mit dieser sehr sensitiven Methode, die nur ca. 10–1000 Milliarden Atome eines radioaktiven Isotops pro Messung benötigt, können Materialeigenschaften in der lokalen Struktur, Phasenübergänge, Magnetismus und Diffusion untersucht werden. Die PAC-Methode ist verwandt mit der Kernspinresonanz und dem Mößbauer-Effekt, jedoch zeigt sie keine Signalabschwächung bei sehr hohen Temperaturen. Heute wird hauptsächlich die zeit-differenzielle PAC (TDPAC, englisch time differential perturbed angular correlation) verwendet.

Geschichte und Entwicklung

Koinzidenz-Messungen in vereinfachter Darstellung: a-b.) in 90°- und 180°-Detektorstellung, c.) „Rotation des Kerns“ bzw. eines Kerns mit Quadrupolmoment (siehe Multipol)

PAC geht auf eine theoretische Arbeit von Donald R. Hamilton aus dem Jahr 1940 zurück. Das erste erfolgreiche Experiment wurde von Brady und Deutsch 1947 durchgeführt. Bei diesen ersten PAC-Experimenten wurden im Wesentlichen Spin und Parität von Kernspins untersucht. Es wurde jedoch früh erkannt, dass elektrische und magnetische Felder mit dem Kernmoment wechselwirken, was die Grundlage für eine neue Form der Materialuntersuchungen lieferte: Die nukleare Festkörperspektroskopie.

Schritt für Schritt entwickelt sich die Theorie. Nachdem 1953 Abragam und Pound ihre Arbeiten über die Theorie von PAC veröffentlichten, die extranukleare Felder in der Theorie berücksichtigen, wurden danach viele Untersuchungen mit PAC durchgeführt.

In den 1960er und 1970er Jahren stieg das Interesse an PAC-Experimenten stark an, deren Fokus hauptsächlich magnetische und elektrische Felder in Kristallen waren, in die die Sondenkerne eingebracht wurden. Mitte der 1960er Jahre wurde die Ionenimplantation entdeckt, die neue Möglichkeiten zur Probenherstellung ermöglichte. Die rasante elektronische Entwicklung der 1970er Jahre brachte deutliche Verbesserungen in der Signalverarbeitung. Von den 1980ern bis heute hat sich PAC als eine wichtige Methode zur Untersuchung und Charakterisierung von Materialien entwickelt, z. B. für die Untersuchung von Halbleitermaterialien, zwischenmetallischen Verbindungen, Oberflächen und Grenzflächen. Lars Hemmingsen et al. wendeten PAC zuletzt auch in biologischen Systemen an.

Während bis ca. 2008 PAC-Instrumente konventionelle Hochfrequenzelektronik der 1970er Jahre verwendeten, wurde in 2008 durch Christian Herden und Jens Röder et al. das erste voll-digitalisierte PAC-Instrument entwickelt, dass umfangreiche Datenanalysen sowie den parallelen Einsatz mehrerer Sonden ermöglicht. Nachbauten und weitere Entwicklungen folgten.

Messprinzip

Zerfallsschema von ¹¹¹In, das nach ¹¹¹Cd zerfällt mit einem 5/2⁺-Zwischenzustand.

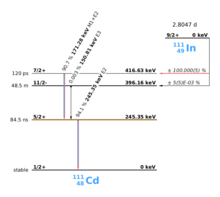
PAC nutzt radioaktive Sonden, die beim Zerfall einen Zwischenzustand mit Lebensdauern von 2 ns bis ca. 10 µs besitzen, siehe Beispiel ¹¹¹In im Bild rechts. Nach dem Elektroneneinfang (EC, electron capture) transmutiert Indium zu Cadmium. Unmittelbar danach befindet sich der Cadmium-Kern überwiegend im angeregten 7/2⁺-Kernspin und nur zu einem ganz kleinen Teil im 11/2⁻-Kernspin, letzterer soll nicht weiter betrachtet werden. Der 7/2⁺ angeregte Zustand geht durch Aussenden eines γ-Quants mit 171 keV in den 5/2⁺-Zwischenzustand über, der eine Lebensdauer von 84,5 ns besitzt und der sensitive Zustand für die PAC ist. Dieser Zustand wiederum zerfällt in den 1/2⁺-Grundzustand durch aussenden eines γ-Quants mit 245 keV. PAC detektiert nun beide γ-Quanten und wertet das erste als Start-Signal, das zweite als Stop-Signal.

PAC-Einzelspektren in 90° (d21.dat) und 180° (d24.dat) Detektoranordnung.

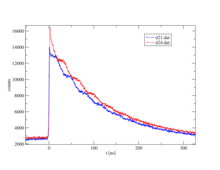
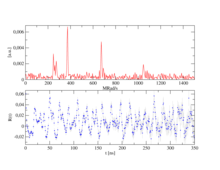
Nun misst man die Zeit zwischen Start und Stopp für jedes Ereignis. Man spricht hier von einer Koinzidenz, wenn ein Start- und Stopp-Paar gefunden wurde. Da der Zwischenzustand nach den Gesetzen des radioaktiven Zerfalls zerfällt, erhält man nach dem Auftragen der Häufigkeit über der Zeit eine exponentielle Kurve mit der Lebensdauer dieses Zwischenzustandes. Aufgrund der nicht-kugelsymmetrischen Ausstrahlung des zweiten γ-Quants, die sogenannte Anisotropie, die eine intrinsische Eigenschaft des Kerns in diesem Übergang ist, kommt es mit den ihm umgebenden elektrischen oder/und magnetischen Feldern zu einer periodischen Störung (Hyperfeinwechselwirkung). Die Abbildung der Einzelspektren rechts zeigt den Effekt dieser Störung als Wellenverlauf auf dem exponentiellen Zerfall von je zwei Detektoren, ein Paar in 90° und eins in 180° zueinander. Die Wellenverläufe zu beiden Detektorpaaren sind gegeneinander verschoben. Sehr vereinfacht kann man sich vorstellen, dass ein fest stehender Beobachter einen Leuchtturm betrachtet, dessen Lichtintensität periodisch heller und dunkler wird. Entsprechend „sieht“ eine Detektoranordnung, meist 4 Detektoren in planarer 90°-Anordnung oder 6 Detektoren in oktaedrischer Anordnung, die Rotation des Kerns in Größenordnungen von MHz bis GHz.

Unten: komplexes PAC-Spektrum einer polykristallinen Substanz, oben: Fouriertransformation

PAC-Spektrum der ^111mCd-Sonde in einem ZnO-Einkristall, mit Fit.

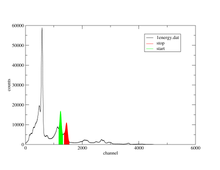
Nach der Anzahl n der Detektoren, ergibt sich die Anzahl der Einzelspektren (z) nach z=n²−n, für n=4 daher 12 und für n=6 somit 30. Um ein PAC-Spektrum zu erhalten, werden die 90°- und 180°-Einzelspektren so miteinander verrechnet, dass die exponentiellen Funktionen sich aufheben und zusätzlich die unterschiedlichen Detektoreigenschaften sich herauskürzen. Es bleibt die reine Störfunktion übrig, wie in dem Beispiel eines komplexen PAC-Spektrums gezeigt ist. Seine Fouriertransformation ergibt die Übergangsfrequenzen als Peaks.

$R(t)$, das Zählratenverhältnis wird wie folgt berechnet:

$R(t)=2{\frac {W(180^{\circ },t)-W(90^{\circ },t)}{W(180^{\circ },t)+2W(90^{\circ },t)}}$

Je nach Spin des Zwischenzustandes zeigen sich eine unterschiedliche Anzahl von Übergangsfrequenzen. Für 5/2 Spin sind 3 Übergangsfrequenzen zu beobachten mit dem Verhältnis ω₁+ω₂=ω₃. Für jeden zugehörigen Gitterplatz der Einheitszelle ist in der Regel eine andere Kombination von 3 Frequenzen zu beobachten.

PAC ist eine statistische Methode: Jedes radioaktive Sondenatom sitzt in seiner eigenen Umgebung. In Kristallen sind aufgrund der hohen Regelmäßigkeit der Anordnung der Atome oder Ionen die Umgebungen identisch oder sehr ähnlich, so dass Sonden auf identischen Gitterplätzen die gleiche Störgröße erfahren, die dann erst in einem PAC-Spektrum messbar wird. Befinden sich die Sonden hingegen in sehr unterschiedlichen Umgebungen, wie z. B. in amorphen Materialien, ist in der Regel eine breite Frequenzverteilung oder gar keine erkennbar und das PAC-Spektrum erscheint flach, ohne Frequenzverlauf. Bei Einkristallen können je nach Orientierung des Kristalls zu den Detektoren bestimmte Übergangsfrequenzen vermindert oder ausgelöscht werden, wie im Beispiel des PAC-Spektrums von Zinkoxid (ZnO) zu sehen ist.

Instrumenteller Aufbau

PAC-Aufbau

Energiespektrum von ¹⁴⁹Gd mit Energiefenstern für start und stop.

Beim typischen PAC-Spektrometer sind 4 Detektoren in planarer 90°- und 180°-Anordnung oder 6 Detektoren in oktaedrischer Anordnung um die Probe mit radioaktiver Quelle platziert. Als Detektoren werden Szintiallationskristalle aus BaF₂ oder NaI verwendet. Bei modernen Instrumenten kommen heute überwiegend LaBr₃:Ce oder CeBr₃ zum Einsatz. Photomultiplier wandeln die schwachen Lichtblitze in elektrische Signale um, die im Szintillator durch Gammastrahlung erzeugt wurden. In klassischen Instrumenten werden diese Signale verstärkt und in logischen UND/ODER Schaltungen in Kombination mit Zeitfenstern den verschiedenen Detektorkombinationen (für 4 Detektoren: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43) zugeordnet und gezählt. Moderne digitale Spektrometer verwenden Digitizer-Karten, die das Signal direkt verwenden und in Energie- und Zeitwerte umwandeln und auf Festplatten speichern. Diese werden dann per Software nach Koinzidenzen durchsucht. Während bei klassischen Instrumenten für die jeweiligen γ-Energien begrenzende „Fenster“ vor der Verarbeitung gesetzt werden müssen, ist dies bei der digitalen PAC während des Aufzeichnens der Messung nicht notwendig und erfolgt erst im Analyseschritt. Bei Sonden mit komplexen Kaskaden ist es dadurch möglich, eine Datenoptimierung vorzunehmen oder mehrere Kaskaden parallel auszuwerten, sowie verschiedene Sonden gleichzeitig zu messen. Die dabei anfallenden Datenmengen können pro Messung zwischen 60 und 300 GB betragen.

Probenmaterialien

Als Materialien für die Untersuchung (Proben) eignen sich prinzipiell alle Materialien, die fest und flüssig sein können. Je nach Fragestellung und Ziel der Untersuchung ergeben sich bestimmte Rahmenbedingungen. Für die Beobachtung klarer Störfrequenzen ist es aufgrund der statistische Methode notwendig, dass ein gewisser Anteil der Sondenatome sich in einer ähnlichen Umgebung befindet und z. B. denselben elektrischen Feldgradienten erfährt. Ferner darf sich während des Zeitfensters zwischen dem Start und Stop, oder grob ca. 5 Halbwertszeiten des Zwischenzustandes, die Richtung des elektrischen Feldgradienten nicht ändern. In Flüssigkeiten wird deshalb infolge der häufigen Stöße keine Störfrequenz messbar, es sei denn, die Sonde befindet sich komplexiert in großen Molekülen, wie z. B. in Proteinen. Die Proben mit Proteinen oder Peptiden werden zur Verbesserung der Messung meist eingefroren.

Die am meisten untersuchten Materialien mit PAC sind Festkörper wie Halbleiter, Metalle, Isolatoren und verschiedene Arten funktioneller Materialien. Für die Untersuchungen liegen diese meist kristallin vor. Amorphe Materialien besitzen keine hochgeordneten Strukturen. Sie besitzen jedoch eine Nahordnung, die sich in der PAC-Spektroskopie als breite Verteilung von Frequenzen zeigen kann. Nano-Materialien haben nach dem Core-Shell-Modell einen kristallinen Kern und eine Hülle, die eine eher amorphe Struktur besitzt. Je kleiner das Nanoteilchen wird, umso größer wird der Volumenanteil dieses amorphen Anteils. In PAC-Messungen zeigt sich dies mit der Abnahme des kristallinen Frequenzanteils in einer Verringerung der Amplitude (Dämpfung).

Probenherstellung

Die für eine Messung benötigte Menge an geeigneten PAC-Isotopen liegt zwischen ca. 10 bis 1000 Milliarden Atomen (10¹⁰–10¹²). Die richtige Menge hängt von den jeweiligen Eigenschaften des Isotops ab. 10 Milliarden Atome sind eine sehr kleine Stoffmenge. Zum Vergleich enthält ein Mol ca. 6,22·10²³ Teilchen. 10¹² Atome in einem Kubikzentimeter Beryllium ergeben eine Konzentration von ca. 8 nmol/L (Nanomol = 10⁻⁹ mol). Die radioaktiven Proben haben je eine Aktivität von 0,1–5 MBq, was in der Größenordnung der Freigrenze für das jeweilige Isotop liegt.

Wie die PAC-Isotope in die zu untersuchende Probe gebracht werden, obliegt dem Experimentator und den technischen Möglichkeiten. Es sind folgende Methoden üblich:

Implantation

Schematische Darstellung des Isotope Separator On Line DEvice (ISOLDE) am CERN. Der Protonenstrahl des Proton Synchrotron Boosters (PSB) erzeugt in den Targets radioaktive Nuklide. Diese werden in den Ionenquellen ionisiert, beschleunigt und mit den Ablenkmagneten des GPS (General Purpose Separator) oder HRS (High Resolution Separator) aufgrund ihrer unterschiedlichen Massen getrennt.

Bei der Implantation wird ein radioaktiver Ionenstrahl erzeugt, der auf das Probenmaterial gerichtet ist, wie z. B. an ISOLDE. Durch die kinetische Energie der Ionen (1–500 keV) fliegen diese in das Kristallgitter und werden durch Stöße abgebremst. Sie kommen entweder auf Zwischengitterplätzen zum Stehen oder stoßen ein Gitteratom von seinem Platz und ersetzen dieses. Dies führt zu einer Störung der Kristallstruktur. Diese Störungen können mit PAC untersucht werden. Durch Temperieren können diese Störungen ausgeheilt werden. Sollen hingegen Strahlendefekte im Kristall und deren Ausheilung untersucht werden, misst man unausgeheilte Proben, die dann schrittweise ausgeheilt werden.

Die Implantation ist meist die Methode der Wahl, weil mit ihr sehr gut definierte Proben hergestellt werden können.

Überdampfen

Im Vakuum kann die PAC-Sonde auf die Probe aufgedampft werden. Die radioaktive Sonde wird dazu auf einer Heizplatte oder Glühlwendel aufgetragen, dort auf die Verdampfungstemperatur gebracht und auf dem gegenüberliegenden Probenmaterial kondensiert. Mit dieser Methode können z. B. Oberflächen untersucht werden. Weiterhin können durch Aufdampfen weiterer Materialien Grenzflächen hergestellt werden, deren Verhalten beim Temperieren mit PAC studiert werden kann. Ebenso kann die PAC-Sonde beim Sputtern übertragen werden mit Hilfe eines Plasmas.

Diffusion

Bei der Diffusionsmethode wird die radioaktive Sonde meist in einem Lösungsmittel verdünnt auf die Probe aufgebracht, eingetrocknet und sie wird durch Temperieren in das Material eindiffundiert. Die Lösung mit der radioaktiven Sonde sollte dabei möglichst rein sein, da auch alle anderen Substanzen mit in die Probe eindiffundieren können und dadurch das Messergebnis beeinflusst wird. Die Probe sollte ausreichend in der Probe verdünnt sein. Daher sollte der Diffusionsvorgang sollte so geplant sein, dass eine möglichst gleichmäßige Verteilung oder ausreichende Eindringtiefe erreicht wird.

Einbau während der Synthese

PAC-Sonden können auch während der Synthese von Probenmaterialien beigegeben werden, um eine möglichst gleichmäßige Verteilung in der Probe zu erreichen. Diese Methode ist besonders gut geeignet, wenn beispielsweise die PAC-Sonde nur schlecht im Material diffundiert und eine höhere Konzentration an Korngrenzen zu erwarten ist. Da bei PAC nur sehr kleine Proben notwendig sind (ca. 5 mm), können Mikro-Ansätze verwendet werden. Ideal wird die Sonde der flüssigen Phase des Sol-Gel-Prozesses beigegeben oder einer der späteren Präkursor-Phasen.

Neutronenaktivierung

Bei der Neutronenaktivierung wird die Sonde direkt aus dem Probenmaterial hergestellt, indem durch Neutroneneinfang in sehr geringer Teil eines der Elemente des Probenmaterials in die gewünschte PAC-Sonde oder sein Mutterisotop umgewandelt wird. Wie auch bei der Implantation müssen Strahlenschäden ausgeheilt werden. Diese Methode beschränkt sich auf Probenmaterialien, die Elemente enthalten, aus denen durch Neutroneneinfang PAC-Sonden hergestellt werden können. Ferner können Proben mit solchen Elementen gezielt verunreinigt werden, das aktiviert werden soll. Beispielsweise eignet sich Hafnium für die Aktivierung ausgezeichnet wegen seines großen Einfangquerschnitts für Neutronen.

Kernreaktionen

Selten verwendet werden direkte Kernreaktionen, bei denen durch Beschuss durch hochenergetischen Elementarteilchen oder Protonen Kerne in PAC-Sonden umgewandelt werden. Hierbei treten große Strahlenschäden auf, die ausgeheilt werden müssen. Diese Methode wird bei PAD verwendet, die zu den PAC-Methoden gehört.

Labore

Das aktuell weltweit größte PAC-Labor befindet sich an der ISOLDE im CERN mit ca. 10 Instrumenten, das wesentlich vom BMBF gefördert wird. An der ISOLDE werden radioaktive Ionenstrahlen hergestellt, indem Protonen aus dem Booster auf Target-Materialien (Urancarbid, flüssiges Zinn usw.) geschossen werden und die Spallationsprodukte bei hohen Temperaturen verdampft (bis zu 2000 °C), dann ionisiert und anschließend beschleunigt werden. Mit der anschließenden Massenseparation können meist sehr reine Isotopenstrahlen hergestellt werden, die in PAC-Proben implantiert werden können. Von besonderem Interesse für die PAC sind dort kurzlebige Sonden wie: ^111mCd, ^199mHg, ^204mPb, sowie verschiedene Sonden der seltenen Erden.

Theorie

Allgemeine γ-γ-Kaskade mit Lebensdauer $\tau _{N}$ des Zwischenniveaus.

Das erste $\gamma$-Quant ($\gamma _{1},k_{1}$) wird isotrop ausgestrahlt. Durch die Detektion dieses Quants in einem Detektor wird aus den vielen möglichen Richtungen eine Teilmenge herausgesucht, die eine gegebene Orientierung hat. Das zweite $\gamma$-Quant ($\gamma _{2},k_{2}$) wird anisotrop ausgestrahlt und zeigt den Effekt der Winkelkorrelation. Das Ziel ist die relative Wahrscheinlichkeit $W(\Theta ){\textrm {d}}(\Omega )$ mit der Detektion von $\gamma _{2}$ im feststehenden Winkel $\Theta$ in Bezug zu $\gamma _{1}$ zu bestimmen (Störungstheorie). Die Wahrscheinlichkeit ist gegeben mit der Winkelkorrelation:

$W(\Theta )=\sum _{k}^{k_{\text{max}}}A_{kk}P_{k}\cos(\Theta )$

Für eine $\gamma$-$\gamma$-Kaskade ist $k$ gerade aufgrund der Konservierung der Parität sowie:

$0<k<{\text{min}}(2I_{S},I_{i}+I'_{i})$

Dabei ist $I_{S}$ der Spin des Zwischenzustandes und $I_{i}$ mit $i=1;2$ die Multipolarität der zwei Übergänge. Für reine Multipolübergänge ist $I_{i}=I'_{i}$.

$A_{kk}$ ist der Anisotropiekoeffizient, der abhängig ist vom Drehimpuls des Zwischenzustands und den Multipolaritäten des Überganges.

Der radioaktive Kern ist für Untersuchungen im Probenmaterial eingebaut und sendet beim Zerfall zwei $\gamma$-Quanten aus. Während der Lebensdauer des Zwischenzustandes, also der Zeit zwischen $\gamma _{1}$ und $\gamma _{2}$, erfährt der Kern aufgrund der Hyperfeinwechselwirkung durch seine elektrische und magnetische Umgebung eine Störung. Durch diese Störung ändert sich die Winkelkorrelation nach:

$W(\Theta )=\sum _{k}^{k_{\text{max}}}A_{kk}G_{kk}$

$G_{kk}$ ist der Störfaktor. Aufgrund der elektrischen und magnetischen Wechselwirkung erfährt der Drehimpuls des Zwischenzustandes $I_{i}$ um seine Symmetrieachse ein Drehmoment. Quantenmechanisch bedeutet dies, dass die Wechselwirkung zu Übergängen zwischen dem M-Zuständen führt. Das zweite $\gamma$-Quant ($\gamma _{2}$) wird dann von einem Niveau mit geänderter Population ausgesandt. Diese Populationsänderung ist der Grund für die Dämpfung der Korrelation.

Die Wechselwirkung findet zwischen dem magnetischen Kerndipolmoment ${\vec {\nu }}$ und dem Zwischenzustand $I_{S}$ oder/und einem äußeren magnetischen Feld ${\vec {B}}$ statt. Die Wechselwirkung findet auch statt zwischen Kernquadrupolmoment und dem außerkernischen elektrischen Feldgradienten $V_{zz}$.

Magnetische Dipolwechselwirkung

Für die magnetische Dipolwechselwirkung ist die Frequenz der Präzession des Kernspins um die Achse des magnetischen Felds ${\vec {B}}$:

$\omega _{L}={\frac {g\cdot u_{N}\cdot B}{\hbar }}$

$\Delta E=\hbar \cdot \omega _{L}=-g\cdot u_{N}\cdot B$

$g$ ist der Landé-Faktor und $u_{N}$ ist das Kernmagneton.

Mit $N=M-M'$ ergibt sich:

$E_{\text{magn}}(M)-E_{\text{magn}}(M')=-(M-M')g\mu _{N}B_{z}=N\hbar \omega _{L}$

Aus der allgemeinen Theorie wird dann erhalten:

$G_{k_{1}k_{2}}^{NN}={\sqrt {(2k_{1}+1)(2k_{2}+1)}}\cdot e^{-iN\omega _{L}t}\times \sum _{M}{\begin{pmatrix}I&I&k_{1}\\M'&-M&N\\\end{pmatrix}}{\begin{pmatrix}I&I&k_{2}\\M'&-M&N\\\end{pmatrix}}$

Für die magnetische Wechselwirkung ergibt sich dann:

$G_{k_{1}k_{2}}^{NN}=e^{\left({-iN\omega _{L}t}\right)}$

Statische elektrische Quadrupolwechselwirkung

Die Energie der elektrischen Hyperfeinwechselwirkung zwischen der Ladungsverteilung des Kerns und dem extranuklearen statischen elektrischen Feld kann zu Multipolen erweitert werden. Der Monopolterm bewirkt lediglich eine Energieverschiebung und der Dipolterm verschwindet, sodass der erste relevante Expansionsterm der Quadrupolterm ist:

$E_{Q}=\sum _{ij}Q_{ij}V_{ij}$     ij=1;2;3

Dieser kann als Produkt des Quadrupolmomentes $Q_{ij}$ und des elektrischen Feldgradienten $V_{ij}$ geschrieben werden. Beide Tensoren sind von zweiter Ordnung. Höhere Ordnungen haben einen zu kleinen Effekt, um mit PAC gemessen werden zu können.

Der elektrische Feldgradient ist die zweite Ableitung des elektrischen Potentials $\Phi ({\vec {r}})$ am Kern:

$V_{ij}={\frac {\partial ^{2}\Phi ({\vec {r}})}{\partial x_{i}\partial x_{j}}}={\begin{pmatrix}V_{xx}&0&0\\0&V_{yy}&0\\0&0&V_{zz}\\\end{pmatrix}}$

$V_{ij}$ wird so diagonalisiert, dass:

$|V_{zz}|\geq |V_{yy}|\geq |V_{xx}|$

Die Matrix ist spurenfrei im Hauptachsensystem (Laplace-Gleichung):

$V_{xx}+V_{yy}+V_{zz}=0$

Üblicherweise wird der elektrische Feldgradient mit dem größten Anteil $V_{zz}$ und $\eta$ definiert:

$\eta ={\frac {V_{yy}-V_{xx}}{V_{zz}}}$,        $0\leq \eta \leq 1$

In kubischen Kristallen sind die Achsenparameter der Elementarzelle x,y,z gleich lang. Daher ist auch $V_{zz}=V_{yy}=V_{xx}$ und $\eta =0$ In axialsymmetrischen Systemen ist ebenfalls $\eta =0$.

Für axialsymmetrische elektrische Feldgradienten nimmt die Energie der Unterzustände die Werte an:

$E_{Q}={\frac {eQV_{zz}}{4I(2I-1)}}\cdot (3m^{2}-I(I+1))$

Die Energiedifferenz zwischen zwei Unterzuständen, $M$ und $M'$, ist gegeben nach:

$\Delta E_{Q}=E_{m}-E_{m'}={\frac {eQV_{zz}}{4I(2I-1)}}\cdot 3|M^{2}-M'^{2}|$

Die Quadrupolfreuquenz $\omega _{Q}$ wird eingeführt. Die Formeln in den farbigen Rahmen sind wichtig für die Auswertung:

:$\omega _{Q}={\frac {eQV_{zz}}{4I(2I-1)\hbar }}={\frac {2\pi eQV_{zz}}{4I(2I-1)h}}={\frac {2\pi \nu _{Q}}{4I(2I-1)}}$

:$\nu _{Q}={\frac {eQ}{h}}V_{zz}={\frac {4I(2I-1)\omega _{Q}}{2\pi }}$

In den Veröffentlichungen ist überwiegend $\nu _{Q}$ angegeben. $e$ als Elementarladung und $h$ als Planck-Konstante sind gut bekannt oder fest definiert. Das Kernquadrupolmoment $Q$ ist häufig nur sehr ungenau bestimmt (oft nur mit 2–3 Stellen). Da $\nu _{Q}$ viel genauer bestimmt werden kann als $Q$, ist es aufgrund der Fehlerfortpflanzung nicht sinnvoll, nur $V_{zz}$ anzugeben. Zudem ist $\nu _{Q}$ unabhängig vom Spin. Das bedeutet, dass Messungen von zwei Isotopen desselben Elements miteinander verglichen werden können, wie z. B. ^199mHg(5/2⁻), ^197mHg(5/2⁻) und ^201mHg(9/2⁻). Weiterhin kann $\nu _{Q}$ als Fingerprint-Methode eingesetzt werden.

Die Energiedifferenz ergibt sich dann nach:

$\Delta E_{Q}=\hbar \omega _{Q}\cdot 3|m^{2}-m'^{2}|$

Wenn $\eta =0$ ist, gilt:

$\omega ^{n}=n\cdot \omega _{Q}^{0}$

mit:

$\omega _{Q}^{0}={\textrm {min}}\left({\frac {\Delta E_{Q}}{\hbar }}\right)$

Für ganzzahlige Spins gilt:

$\omega _{Q}^{0}=3\cdot \omega _{Q}$         und          $n=|M^{2}-M'^{2}|$

Für halbe Spins gilt:

$\omega _{Q}^{0}=6\cdot \omega _{Q}$          und          $n={\frac {1}{2}}|M^{2}-M'^{2}|$

Für den Störfaktor ergibt sich:

$G_{k_{1}k_{2}}^{NN}=\sum _{n}s_{nN}^{k_{1}k_{2}}\cos {(n\omega _{Q}^{0}t)}$

mit dem Faktor für die Gewichtung der beobachteten Frequenzen:

$s_{nN}^{k_{1}k_{2}}={\sqrt {(2k_{1}+1)(2k_{2}+1)}}\cdot \sum _{M,M'}{\begin{pmatrix}I&I&k_{1}\\M'&-M&N\\\end{pmatrix}}{\begin{pmatrix}I&I&k_{2}\\M'&-M&N\\\end{pmatrix}}$

Was die magnetische Dipolwechselwirkung betrifft, induziert auch die elektrische Quadrupolwechselwirkung eine Präzision der Winkelkorrelation in der Zeit und dies moduliert die Quadrupolwechselwirkungsfrequenz. Diese Frequenz ist eine Überlappung der verschiedenen Übergangsfrequenzen $\omega _{n}$. Die relativen Amplituden der verschiedenen Komponenten hängen von der Ausrichtung des elektrischen Feldgradienten relativ zu den Detektoren (Symmetrieachse) und vom Asymmetrieparameter $\eta$ ab. Für eine Untersuchung mit verschiedenen Kernen benötigt man einen Parameter, der einen direkten Vergleich ermöglicht: Daher wird die vom Kernspin ${\vec {I}}$ unabhängige Quadrupolekopplungskonstante $\nu _{Q}$ eingeführt.

Kombinierte Wechselwirkung

Wenn am radioaktiven Kern gleichzeitig eine magnetische und elektrische Wechselwirkung vorliegt, ergeben sich kombinierte Wechselwirkungen, wie oben beschrieben. Dies führt zu Aufspaltung der jeweils beobachteten Frequenzen. Die Analyse ist gegebenenfalls nicht trivial aufgrund der hohen Anzahl von Frequenzen, die zugeordnet werden müssen. Diese hängen dann jeweils von der Richtung des elektrischen und magnetischen Feldes zueinander im Kristall ab. PAC ist eine der wenigen Methoden, mit der diese Richtungen bestimmt werden können.

Dynamische Wechselwirkungen

Fluktuiert während der Lebensdauer $\tau _{n}$ des Zwischenniveaus das Hyperfeinfeld aufgrund von Sprüngen der Sonde in eine andere Gitterposition oder von Sprüngen eines nahen Atoms in eine andere Gitterposition, so geht die Korrelation verloren. Für den einfachen Fall mit einem ungestörten Gitter kubischer Symmetrie gilt bei einer Sprungrate von $\omega _{s}<0{,}2\cdot \nu _{Q}$ für $N_{s}$ äquivalente Plätze eine exponentielle Dämpfung des statischen $G_{22}(t)$-Terms:

$G_{22}^{\text{dyn}}(t)=e^{-\lambda _{d}t}G_{22}(t)$            $\lambda _{d}=(N_{s}-1)\omega _{s}$

Hier ist $\lambda _{d}$ eine zu bestimmende Konstante, die nicht mit der Zerfallskonstante $\lambda ={\frac {1}{\tau }}$ verwechselt werden darf. Bei großen Werten von $\omega _{s}$, ist nur noch der reine exponentielle Abfall zu beobachten:

$G_{22}^{\text{dyn}}(t)=e^{-\lambda _{d}t}$

Der Grenzfall nach Abragam-Pound ergibt sich für $\lambda _{d}$, wenn $\omega _{s}>3\cdot \nu _{Q}$ ist:

$\lambda _{d}\approx {\frac {2{,}5\nu _{Q}^{2}}{N_{s}\omega _{s}}}$

Nachwirkungen bei Transmutation

Zerfallsschema von ¹¹¹In nach ¹¹¹Cd mit Veranschaulichung der Anfangsbesetzungswahrscheinlichkeiten zwischen einem statischen Cd²⁺ und einem dynamischen hochionisierten Zustand Cd^x+.

Kerne, die vor der $\gamma$-$\gamma$-Kaskade transmutieren, führt dies meist zu einer Ladungsänderung in ionischen Kristallen (In³⁺ zu Cd²⁺). In der Folge muss das Gitter auf diese Änderungen reagieren. Dabei können auch Defekte oder Nachbarionen wandern. Ebenso kann durch den hochenergetischen Zerfallsprozess durch den Auger-Effekt der Kern in höhere Ionisierungszustände gebracht werden. Die Normalisierung des Ladungszustandes hängt dann von der Leitfähigkeit des Materials ab. In Metallen findet der Prozess sehr schnell statt. In Halbleitern und Isolatoren dauert dies erheblich länger. Bei all diesen Prozessen ändert sich das Hyperfeinfeld. Fällt diese Änderung in die $\gamma$-$\gamma$-Kaskade, kann sie als Nacheffekt (engl.: aftereffect) beobachtet werden.

Die Anzahl der Kerne im Zustand (a) im Bild rechts wird sowohl durch den Zerfall nach Zustand (b) als auch nach Zustand (c) depopuliert:

$\mathrm {d} N_{a}=-N_{a}\left(\Gamma _{r}+{\frac {1}{\tau _{7/2}}}\right)\mathrm {d} t$

mit: $\tau _{7/2}={\frac {120\,{\text{ps}}}{\ln {2}}}$

Daraus erhält man den exponentiellen Fall:

$N_{a}(t)=N_{a_{0}}\cdot e^{\left({-(\Gamma _{r}+{\frac {1}{\tau _{7/2}}})t}\right)}$

Für die Gesamtzahl der Kerne im statischen Zustand (c) folgt dann:

$N_{c}(t)=\Gamma _{r}\int \limits _{0}^{t}N_{a}(t)\mathrm {d} t=N_{0}{\frac {\Gamma _{r}\tau _{7/2}}{\Gamma _{r}\tau _{7/2}+1}}\left(1-e^{-(\Gamma _{r}+{\frac {1}{\tau _{7/2}}})t}\right)$

Die Anfangsbesetzungswahrscheinlichkeiten $\rho$ ergeben sich für statische und dynamische Umgebung zu:

$\rho _{\text{stat}}={\frac {\Gamma _{r}\tau _{7/2}}{\Gamma _{r}\tau _{7/2}+1}}$

$\rho _{\text{dyn}}={\frac {1}{\Gamma _{r}\tau _{7/2}+1}}$

Allgemeine Theorie

Allgemeine γ-γ-Kaskade mit Lebensdauer $\tau _{N}$ des Zwischenniveaus.

In der allgemeinen Theorie ist für einen Übergang $M_{i}\rightarrow M_{f}$ gegeben:

$W(M_{i}\rightarrow M_{f})=\left|\sum _{M}\langle M_{f}|{\mathcal {H}}_{2}|M\rangle \langle M|{\mathcal {H}}_{1}|M_{i}\rangle \right|^{2}$

$W({\vec {k}}_{1},{\vec {k}}_{2})=\sum _{M_{i},M_{f},\sigma _{1},\sigma _{2}}\left|\sum _{M}\langle M_{f}|{\mathcal {H}}_{2}|M\rangle \langle M|{\mathcal {H}}_{1}|M_{i}\rangle \right|^{2}$

$W({\vec {k}}_{1},{\vec {k}}_{2})=W(\Theta )=\sum _{k_{\text{gerade}}}^{k_{\text{max}}}A_{k}(1)A_{k}(2)P_{k}(\cos {\Theta })$

$0\leq k\leq$ Minimum von $(2I,l_{1}+l_{1}',l_{2}+l_{2}')$

Detektorwinkel

$W(\Theta ,t)=\sum _{k=2,4}A_{kk}P_{k}(\cos {\Theta })$

$|M_{a}\rangle \rightarrow \Lambda (t)|M_{a}=\sum _{M_{b}}|M_{b}\rangle \langle M_{b}|\Lambda (t)|M_{a}\rangle$

$W({\vec {k}}_{1},{\vec {k}}_{2},t)=\sum _{M_{i},M_{f},\sigma _{1},\sigma _{2}}\left|\sum _{M_{a}}\langle M_{f}|{\mathcal {H}}_{2}\Lambda (t)|M_{a}\rangle \langle M_{a}|{\mathcal {H}}_{1}|M_{i}\rangle \right|^{2}=\langle \rho ({\vec {k}}_{2})\rangle _{t}$

$W({\vec {k}}_{1},{\vec {k}}_{2},t)=\sum _{k_{1},k_{2},N_{1},N_{2}}A_{k_{1}}(1)A_{k_{2}}(2){\frac {1}{\sqrt {(2k_{1}+1)(2k_{2}+1)}}}\times Y_{k_{1}}^{N_{1}}(\Theta _{1},\Phi _{1})\cdot Y_{k_{2}}^{N_{2}}(\Theta _{2},\Phi _{2})G_{k_{1}k_{2}}^{N_{1}N_{2}}(t)$

mit:

$G_{k_{1}k_{2}}^{N_{1}N_{2}}=\sum _{M_{a},M_{b}}(-1)^{2I+M_{a}+M_{b}}{\sqrt {(2k_{1}+1)(2k_{2}+)}}\times \langle M_{b}|\Lambda (t)|M_{a}\rangle \langle M_{b}'|\Lambda (t)|M_{a}'\rangle ^{*}\times {\begin{pmatrix}I&I&k_{1}\\M_{a}'&-M_{a}&N_{1}\end{pmatrix}}{\begin{pmatrix}I&I&k_{2}\\M_{b}'&-M_{b}&N_{2}\end{pmatrix}}$