Paradox von Hooper

Paradox von Hooper

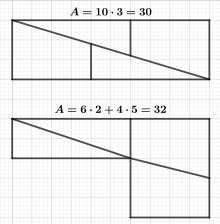
Das Paradox von Hooper ist ein geometrischer Trugschluss, bei dem eine Figur in vier Teile zerlegt wird, die dann zu einem Rechteck zusammengesetzt werden, dessen Flächeninhalt um zwei Flächeneinheiten geringer ist als der Flächeninhalt der Ausgangsfigur.

Analyse des Scheinparadox

Analyse des Paradox von Hooper, das braune Parallelogramm ist die überlappende Fläche der beiden Dreiecke

Bei genauer Betrachtung sieht man, dass die Maße der beiden Dreiecke in der (unteren) Ausgangsfigur nicht mit denen der Dreiecke im Rechteck übereinstimmen. Die kleinere Kathete beträgt exakt 2 Längeneinheiten in der Ausgangsfigur, während sie im Rechteck nur 1,8 Längeneinheiten beträgt. Verwendet man daher die Dreiecke der Ausgangsfigur im Rechteck, so überlappen sie sich ein wenig, wodurch die Fläche eines schmalen Parallelogramms verloren geht. Die Seiten und Diagonalen des Parallelogramms lassen sich mit Hilfe des Satzes von Pythagoras berechnen.

$d_{1}={\sqrt {2^{2}+1^{2}}}={\sqrt {5}}$

$d_{2}={\sqrt {3^{2}+10^{2}}}={\sqrt {109}}$

$s_{1}={\sqrt {2^{2}+6^{2}}}={\sqrt {40}}$

$s_{2}={\sqrt {1^{2}+4^{2}}}={\sqrt {17}}$

Die Fläche des halben Parallelogramms lässt sich mit der Formel von Heron berechnen, dabei erhält man für den halbierten Umfang des Dreiecks beziehungsweise des halben Parallelogramms

$s={\frac {d_{1}+s_{1}+s_{2}}{2}}={\frac {{\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}}}{2}}$

und damit für die Fläche des gesamten Parallelogramms

${\begin{aligned}F&=2\cdot {\sqrt {s\cdot (s-s_{1})\cdot (s-s_{2})\cdot (s-d_{1})}}\\&=2\cdot {\frac {1}{4}}\cdot {\sqrt {({\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}})\cdot (-{\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}})\cdot ({\sqrt {5}}-{\sqrt {17}}+{\sqrt {40}})\cdot ({\sqrt {5}}+{\sqrt {17}}-{\sqrt {40}})}}\\&=2\cdot {\frac {1}{4}}\cdot {\sqrt {16}}\\&=2\end{aligned}}$.

Die scheinbar verschwundene Fläche entspricht also genau der parallelogrammförmigen überlappenden Fläche der vier Zerlegungsteile der Ausgangsfigur.

Geschichte

William Hooper veröffentlichte das nach ihm benannte Scheinparadox 1774 unter dem Titel The geometric money in seinem vierbändigen Werk Rational Recreations allerdings noch mit einer fehlerhaften Zeichnung und Rechnung, die aber in der Ausgabe von 1782 korrigiert wurde. Das Paradox geht jedoch nicht auf Hooper selbst zurück, dessen Buch im Wesentlichen eine Übersetzung der Nouvelles récréations physiques et mathétiques des Franzosen Edmé Gilles Guyot (1706–1786) war. Dieses vierbändige Werk wurde 1769 in Frankreich veröffentlicht und enthielt in seiner Erstausgabe dieselbe falsche Zeichnung und Rechnung.

Literatur

• Martin Gardner: Mathematics, Magic and Mystery. Courier (Dover), 1956, ISBN 9780486203355, S. 129–155
• Greg N. Frederickson: Dissections: Plane and Fancy. Cambridge University Press, 2003, ISBN 9780521525824, Kapitel 23, S. 268–277 insbesondere S. 271–274 (Online-Update zu Kapitel 23)
• Simon During: Modern Enchantments: The Cultural Power of Secular Magic. Harvard University Press, 2004, ISBN 978-0674013711, S. 87
• William Hooper: Rational Recreations. London, 1774, S. 286 (fehlerhafte Erstausgabe)
• William Hooper: Rational Recreations. London, 1782, S. 286 (korrigierte Ausgabe)

Weblinks

• Hooper's Paradox: How Is It Possible? auf cut-the-knot.org
• Mariano Tomatis: Curse of the crystal skulls and other vanishing area puzzles