Peano-Kurve

Die Peano-Kurve (nach Giuseppe Peano) ist eine raumfüllende Kurve (FASS-Kurve).

Sie ist definiert als der Grenzwert einer Folge von Kurven, die schrittweise konstruiert werden können.

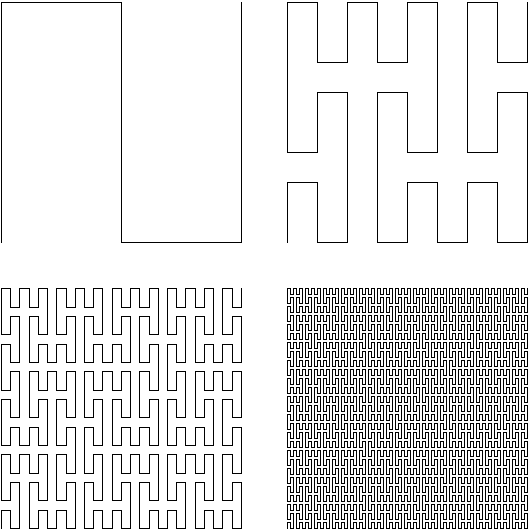
Im zweidimensionalen Fall ist ein Beispiel für eine Peano-Kurve das folgende: Man beginnt mit der Unterteilung eines Quadrats in neun gleich große Quadrate, die in einer S-Kurve durchlaufen werden. Im nächsten Schritt wird jedes dieser Quadrate wieder unterteilt und die entstehenden Quadrate in S-Kurven durchlaufen, die als neue Kurve zusammengehängt werden:

Skaliert man die Kurven auf dieselbe Größe, erhält man als erste vier Schritte:

Setzt man dieses Verfahren der Rekursion fort, erhält man eine Folge von Kurven, die punktweise konvergiert.

Als Grenzwert erhält man die Peano-Kurve, auf der jeder Punkt des Ausgangsquadrats liegt und die unendlich lang ist.

Dieses Verfahren lässt sich leicht auf höhere Dimensionen verallgemeinern. Auch liefert eine stetige surjektive Abbildung $f\colon I\to I^{2}$ (mit $I=[0,1]$) wiederum stetige und surjektive Abbildungen $f\times \operatorname {id} _{I^{n-1}}\colon I^{n}\to I^{n+1}$, und durch Verkettung erhält man eine stetige Surjektion $I\to I^{n}$ für jede natürliche Zahl $n$.

Weitere Peano-Kurven

Es existiert auch noch eine weitere flächenfüllende Kurve, die als „Peano-Kurve“ bekannt ist. Ihre Struktur entspricht der Cantor-Diagonalisierung. Dabei wird eine Strecke zwischen zwei Punkten durch das Gebilde der ersten Stufe ersetzt.

Peano-Kurve der ersten Stufe	Peano-Kurve der zweiten Stufe

Literatur

• Giuseppe Peano: Sur une courbe, qui remplit tout une aire plane. In: Mathematische Annalen 36 (1890), S. 157–160.

Weblinks

Commons: Peano-Kurve – Album mit Bildern, Videos und Audiodateien

• Fraktale Dimension am Beispiel der Peano-Kurve
• Interaktive Demonstration der Peano-Kurve.