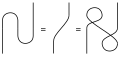Penrosesche graphische Notation

Die penrosesche graphische Notation – auch als penrosesche diagrammatische Notation, Tensor-Diagramm-Notation oder auch einfach Penrose-Notation bezeichnet – ist eine von Roger Penrose vorgeschlagene Notation in der Physik und Mathematik, um eine (meist handschriftliche) visuelle Darstellung multilinearer Abbildungen oder Tensoren zu erhalten. Ein Diagramm besteht hierbei aus geschlossenen Formen, welche über Linien verbunden sind.

Die Notation wurde ausgiebig von Predrag Cvitanović erforscht, welcher diese Notation zur Einstufung klassischer Lie-Gruppen verwendet. Die Notation wurde generalisiert, um die Theorie zu Spin-Netzwerken in der Physik sowie die Präsenz von Matrix-Gruppen in der linearen Algebra darzustellen.

Multilineare Algebra

In der multilinearen Algebra entspricht jede Form einer multilinearen Funktion. Die Linien an Formen repräsentieren die Eingänge oder Ausgänge der Funktion. Die Verbindung dieser Ein- und Ausgänge entspricht der Komposition der jeweiligen Funktionen.

Tensoren

In der Tensoralgebra ist ein bestimmter Tensor als bestimmte Form dargestellt. Linien nach oben und unten abstrahieren obere und untere Indizes der jeweiligen Tensoren. Verbindungen zwischen zwei Formen entspricht der Kontraktion der Indizes. Ein Vorteil dieser Notation ist, dass man nicht neue Buchstaben für neue Indizes erfinden muss. Die Notation ist auch ausdrücklich basisunabhängig.

Beispiele

• 
  Vektor $\xi ^{a}$
• 
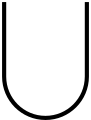
  Vektor $\eta ^{a}$
• 
  Vektor $\zeta ^{a}$
• 
  Vektor $\beta _{a}$
• 
  Tensor $\lambda _{bcd}^{a}$
• 
  Tensor $D_{cd}^{ab}$
• 
  Kronecker-Delta $\delta _{b}^{a}$
• 
  Hermitesches Skalarprodukt
  $\beta _{a}\,\xi ^{a}$$=\langle \xi |\beta \rangle$$=\xi ^{*}\cdot \beta$$=h(\xi ,\beta )$
  (siehe auch: Bra-Ket)
• 
  Metrischer Tensor $g^{ab}$
• 
  Metrischer Tensor $g_{ab}$
• 
  Symmetrisierung $Q^{(a_{1}\ldots a_{n})}$
• 
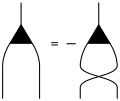
  Asymmetrisierung $E_{[a_{1}\ldots a_{n}]}$
• 
  Tensor $Q_{fg}^{abc}$
• 
  $Q_{fg}^{abc}-2\,Q_{fg}^{bca}$
• 
  $Q_{fg}^{abc}-2\,Q_{gf}^{bca}$
• 
  $\xi ^{a}\,\lambda _{ab[c}^{(d}\,D_{fg]}^{e)b}$
  (mit ${}_{{\frac {1}{2!}}\cdot {\frac {1}{3!}}={\frac {1}{12}}}$)
• 
  Levi-Civita-Symbol (Permutation) $\varepsilon _{a_{1}\ldots a_{n}}$
• 
  $\epsilon ^{a_{1}\ldots a_{n}}$
• 
  Fakultät $\varepsilon _{a_{1}\ldots a_{n}}\,\epsilon ^{a_{1}\ldots a_{n}}=n!$
• 
  Determinante $\det \mathbf {T} =\det \left(T_{\ b}^{a}\right)$
• 
  $\det \left(\mathbf {ST} \right)=$$\det \mathbf {S} \,\det \mathbf {T}$
• 
  $\mathbf {T} ^{-1}=\left(T_{\ b}^{a}\right)^{-1}$
  (Inverse der $n\times n$-Matrix $\mathbf {T}$)
• 
  Spurfunktion $\operatorname {Spur} \mathbf {T} =T_{\ a}^{a}$
• 
  Strukturkonstante $\gamma _{\alpha \beta }^{\chi }=-\gamma _{\beta \alpha }^{\chi }$
• 
  $\gamma _{[\alpha \beta }^{\xi }\,\gamma _{\chi ]\xi }^{\zeta }=0$
• 
  $\gamma _{[\alpha \beta }^{\xi }\,\gamma _{\chi ]\xi }^{\zeta }$$=\gamma _{\alpha \beta }^{\xi }\,\gamma _{\chi \xi }^{\zeta }$$-\gamma _{\alpha \beta }^{\xi }\,\gamma _{\xi \chi }^{\zeta }$$-\gamma _{\xi \beta }^{\zeta }\,\gamma _{\chi \alpha }^{\xi }$$=0$
• 
  Killing-Form $\kappa _{\alpha \beta }$$=\kappa _{\beta \alpha }$$=\gamma _{\alpha \zeta }^{\ \ \xi }\,\gamma _{\beta \xi }^{\ \ \zeta }$
• 
  Kovariante Ableitung $12\nabla _{\mu }\left\{\xi ^{a}\lambda _{ab[c}^{(d}D_{fg]}^{e)b}\right\}$
• 
  Riemannscher Krümmungstensor $R_{abc}^{\ \ \ d}$
• 
  Ricci-Identität $(\nabla _{a}\,\nabla _{b}-\nabla _{b}\,\nabla _{a})\,\mathbf {\xi } ^{d}$$=R_{abc}^{\ \ \ d}\,\mathbf {\xi } ^{c}$
• 
  Ricci-Tensor $R_{ab}=R_{acb}^{\ \ \ c}$
• 
  Antisymmetrie des riemannschen Krümmungstensors $R_{abc}^{\ \ \ d}=-R_{bac}^{\ \ \ d}$
• 
  Bianchi-Symmetrie $R_{[abc]}^{\ \ \ d}$$=R_{abc}^{\ \ \ d}$$+R_{cab}^{\ \ \ d}$$+R_{bca}^{\ \ \ d}$$=0$
• 
  Bianchi-Identität $\nabla _{[a}R_{bc]d}^{\ \ \ e}=0$
• 
  $g_{ab}=g_{ba}$
  (z. B. $\mathbf {g} ^{T}=\mathbf {g}$)
• 
  $g^{ab}=g^{ba}$
• 
  $g_{ab}\,g^{bc}=\delta _{a}^{c}=g^{cb}\,g_{ba}$

Siehe auch

• Abstrakte Index-Notation

Literatur

• Roger Penrose: The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape, London u. a. 2004, ISBN 0-224-04447-8.
• Roger Penrose, Wolfgang Rindler: Spinors and Space-Time: Vol I, Two-Spinor Calculus and Relativistic Fields. Cambridge University Press, 1984, ISBN 0-521-24527-3. 
• Roger Penrose, Wolfgang Rindler: Spinors and Space-Time: Vol. II, Spinor and Twistor Methods in Space-Time Geometry. Cambridge University Press, 1986, ISBN 0-521-25267-9. 

Weblinks

Commons: Penrose graphical notation – Sammlung von Bildern, Videos und Audiodateien