Produktivität

Als Produktivität wird in der Betriebswirtschaftslehre und Volkswirtschaftslehre eine betriebswirtschaftliche bzw. volkswirtschaftliche Kennzahl bezeichnet, die das Verhältnis zwischen produzierten Gütern/Dienstleistungen und den dafür benötigten Produktionsfaktoren beschreibt.

Allgemeines

Die Wirtschaftssubjekte (Privathaushalte, Unternehmen und der Staat mit seinen Untergliederungen wie öffentliche Verwaltung, Staatsunternehmen, Kommunalunternehmen) sind gehalten, mit knappen Ressourcen rational umzugehen (Rationalprinzip). Dazu gehört auch die Produktivität als die Summe von produktiven Maßnahmen der Wirtschaftssubjekte und deren Verhaltensmustern, in der Regel bezogen auf ein System oder einen Produktionsprozess mit Produktionsfaktoren und Produkten. Gemessen am Rationalprinzip ist alles als produktiv einzustufen, bei dem die eingesetzten Ressourcen in einem günstigen Verhältnis zur erzielten Wirkung stehen.^[1] Ist dies nicht der Fall, wird von unproduktiv gesprochen (siehe unproduktive Arbeit). Produktivität ist begrifflich eng verwandt mit der Konstruktivität und dem Gegenteil, der Destruktivität.

Wirtschaftswissenschaftliche Definitionen

In der Volkswirtschaftslehre und Betriebswirtschaftslehre^[2] wird unter Produktivität eine volkswirtschaftliche oder betriebswirtschaftliche Kennzahl verstanden, die das (Mengen-)Verhältnis zwischen dem, was produziert wird (englisch Output), und den dafür beim Produktionsprozess eingesetzten Mitteln (Produktionsfaktoren, englisch Input) wiedergibt.^[3]

Zu ihrer Erfüllung kann entweder mit einem möglichst geringen Input ein gegebener Output (Minimalprinzip) oder mit einem gegebenen Input ein möglichst großer Output (Maximalprinzip) erreicht werden. Damit ist die Produktivität auch eine spezifische Ausprägung des Rationalprinzips. Die Einhaltung der Produktivität als Verhaltensmaxime ermöglicht auch die Erfüllung des Ziels der Gewinnmaximierung oder der Nutzenmaximierung. Zwischen diesen Zielen besteht somit Zielharmonie.

Unterschied zwischen Produktivität und Wirtschaftlichkeit

Während sich die Produktivität mit der Gegenüberstellung von Output und Input befasst, setzt die Wirtschaftlichkeit Kosten/Aufwand zu Ertrag/Erlös miteinander in Beziehung. Der Wirtschaftlichkeit liegen mithin wertmäßige Größen zugrunde, der Produktivität dagegen mengenmäßige.

Faktorproduktivität

Die Faktorproduktivität ist der Quotient aus der Ausbringung, die durch den Einsatz aller Produktionsfaktoren erzielt wird und der Einsatzmenge eines bestimmten Produktionsfaktors (partielle Faktorproduktivität) oder allen Faktorkosten (totale Faktorproduktivität).^[4]

Die partielle Faktorproduktivität bezieht sich auf einen einzigen Produktionsfaktor, so dass es für den Faktor Arbeit die Arbeitsproduktivität, für den Faktor Kapital die Kapitalproduktivität und beim Boden die Bodenproduktivität gibt.

Produktionsfaktor	Faktorproduktivität	Faktorpreis
Arbeit	Arbeitsproduktivität	Arbeitseinkommen
Boden	Bodenproduktivität	Bodenpreis
Kapital	Kapitalproduktivität	Kapitalzins

Dabei ist zu bedenken, dass faktorbezogene Produktivitäten stets das Zusammenwirken aller Produktionsfaktoren reflektieren: in der Arbeitsproduktivität steckt die Leistung eingesetzter Maschinen, in der Kapitalproduktivität ist die Arbeitsleistung der Arbeitskräfte berücksichtigt.^[5] So kann beispielsweise ein Arbeiter mit einem Bagger mehr Erde bewegen als mit einer Schaufel; die Arbeitsproduktivität verbessert sich durch den Kapitaleinsatz, obwohl sich Umfang und Intensität des Arbeitseinsatzes nicht verändert haben.^[6]

Ermittlung

Die Gesamtproduktivität $P$ in Unternehmen wird durch Gegenüberstellung der Ausbringungsmenge $A$ und der Faktoreinsatzmenge $F$ ermittelt:^[7]

{\text{P}}={\frac {\text{A}}{\text{F}}}={\frac {\text{Output}}{\text{Input}}}

.

Dabei wird der Output als Menge pro Zeitspanne angegeben (Ausbringungsmenge), also als eine Stromgröße betrachtet. Der Input kann auch eine Stromgröße sein, beispielsweise die Anzahl der Arbeitsstunden in einem Jahr (Arbeitszeit) oder Abschreibungen in einem Jahr. Er kann auch eine Bestandsgröße sein, beispielsweise durchschnittliche Anzahl der Erwerbstätigen in einem Jahr oder durchschnittlicher Kapitalstock eines Jahres.

Da die erzeugten Güter/Dienstleistungen ganz unterschiedlicher Art sind und sich die Zusammensetzung der Produktion nach verschiedenen Gütern im Zeitablauf auch noch verändern kann, ist es notwendig, die verschiedenen Güter mit Preisen zu bewerten, um den Gesamtoutput als eindimensionale Größe angeben zu können. Hierzu werden die Güter zu Marktpreisen bewertet, sofern solche existieren. Güter, für die es keine Marktpreise gibt, werden zu Herstellungskosten bewertet. Des Weiteren werden beim Output reine Preisveränderungen mit Hilfe von Preisbereinigungsverfahren herausgerechnet. Eine Methode ist etwa das Rechnen in konstanten Preisen eines Basisjahres.

Das gleiche Bewertungsproblem ergibt sich auch bei dem Produktionsfaktor Kapital, da sich der Kapitalstock aus verschiedenen Gütern zusammensetzt. Beim Produktionsfaktor Arbeit wird dagegen auf die physischen Mengen wie Anzahl der Erwerbstätigen oder Anzahl der Arbeitsstunden zurückgegriffen.

Partielle Faktorproduktivitäten

Die partielle Faktorproduktivität lässt sich nach den unterschiedlichen Produktionsfaktoren untergliedern:

{\text{Arbeitsproduktivität}}={\frac {\text{Ausbringungsmenge}}{\text{Eingesetzte Arbeitsstunden}}}

,

{\text{Maschinenproduktivität}}={\frac {\text{Ausbringungsmenge}}{\text{Eingesetzte Maschinenstunden}}}

,

{\text{Materialproduktivität}}={\frac {\text{Ausbringungsmenge}}{\text{Materialeinsatzmenge}}}

{\text{Bodenproduktivität}}={\frac {\text{Erntemenge}}{\text{Landfläche}}}

.

Bei der Ermittlung der partiellen Faktorproduktivität wird die Menge der erzeugten Güter ins Verhältnis zur Einsatzmenge eines bestimmten Produktionsfaktors gesetzt.

Diese so statistisch gemessenen Produktivitäten kann man nicht ursächlich in dem Sinne verstehen, dass etwa eine steigende Arbeitsproduktivität zeigt, dass die Arbeiter „fleißiger“ werden und dass sinkende Kapitalproduktivität zeigt, dass das der zunehmende Kapitaleinsatz immer weniger bringt. Vielmehr ist steigende Arbeitsproduktivität Folge davon, dass je Arbeiter immer mehr Produktionsmittel eingesetzt werden. Typischerweise steigt deshalb langfristig die Arbeitsproduktivität, während die Kapitalproduktivität stagniert oder gar zurückgeht.

In der neoklassischen Theorie gilt die Annahme, dass die Produktionsfaktoren gemäß ihrer Produktivität entlohnt werden – was nicht heißt, dass dieses auch in der Praxis geschieht. Gründe hierfür können in Marktversagen oder Externalitäten liegen. Mit Hilfe der statistisch gemessenen Produktivitäten kann überprüft werden, ob dieses der Fall ist.

Arbeitsproduktivität

Die bekannteste und meistbenutzte Faktorproduktivität ist die Arbeitsproduktivität. Dies liegt insbesondere daran, dass die erforderlichen Daten relativ leicht zu ermitteln sind. Die Arbeitsproduktivität $AP$ gibt das Verhältnis aus der mengenmäßigen Arbeitsleistung (Arbeitsvolumen) $AL$ .und dem mengenmäßigen Arbeitseinsatz $AE$ .wieder:

AP={\frac {AL}{AE}}

.

Sowohl die Ausbringungsmenge ( $AL$ ) als auch die Arbeitseinsatzmenge ( $AE$ ) sind verfügbare Unternehmensdaten, die für Zwecke der Volkswirtschaft aggregiert werden müssen.

Die volkswirtschaftliche Formel für die Arbeitsproduktivität je Arbeitsstunde lautet:

{\text{APi}}={\frac {BIP_{\mathrm {real} }}{\text{Arbeitsvolumen}}}={\frac {BIP_{\mathrm {real} }}{Et\cdot h}}

,

wobei $BIP_{\mathrm {real} }$ das reale Bruttoinlandsprodukt, $Et$ die Anzahl Erwerbstätiger und $h$ die Anzahl der geleisteten Arbeitsstunden je Erwerbstätigen ist.

Die volkswirtschaftliche Formel für die Arbeitsproduktivität je Erwerbstätigem lautet:

{\text{APi}}={\frac {BIP_{\mathrm {real} }}{Et}}

oder

{\text{AP}}={\frac {\text{Ergebnis}}{\text{Arbeitsaufwand}}}

.

Die betriebswirtschaftliche Stundenleistung ergibt sich aus der Gegenüberstellung von Absatzvolumen und geleisteten Arbeitsstunden:

{\text{Stundenleistung}}={\frac {\text{Absatzvolumen}}{\text{Arbeitsstunden}}}

.

Erhöht sich bei konstanten Arbeitsstunden das Absatzvolumen, hat sich die produktive Stundenleistung verbessert und umgekehrt.

{\text{Beschäftigtenproduktivität}}={\frac {\text{Gesamtumsatz }}{\text{Anzahl der tätigen Mitarbeiter}}}

.

Dieser Wert gibt an, wie sich der Gesamtumsatz pro Mitarbeiter darstellt, also wie viel im Durchschnitt der einzelne Mitarbeiter zum Gesamtumsatz beigetragen hat. In Deutschland liegt der Durchschnitt dieses Wertes ungefähr bei 50.000 bis 70.000 Euro pro Mitarbeiter.

Bodenproduktivität

Als Bodenproduktivität wird in der Land- und Forstwirtschaft die Produktivität des Produktionsfaktors Boden bezeichnet. Sie ist der auf die Nutzfläche bezogene Bodenertrag.^[8] Die Bodenproduktivität $BP$ gibt das Verhältnis aus Bodenertrag $BE$ und der dafür erforderlichen Landfläche $Lf$ .wieder:^[9]

BP={\frac {BE}{Lf}}

.

Als Berechnungseinheit dient die Landfläche von 1 Hektar. Werden auf einer Landfläche von 1 Hektar 3 Tonnen Weizen geerntet und auf einer anderen Fläche 4 Tonnen im gleichen Zeitraum, so weist die letztere eine höhere Bodenproduktivität auf.

Kapitalproduktivität

Die Kapitalproduktivität $KP$ ist das Verhältnis zwischen dem gesamtwirtschaftlichen Bruttoinlandsprodukt (BIP) $Yr$ und dem Kapitalstock $K$ :^[10]

KP={\frac {Yr}{K}}

.

Sinkt die Kapitalproduktivität, wurde im Zeitablauf vermehrt Kapital für die gleiche Produktionsmenge an Gütern und Dienstleistungen eingesetzt, so dass der Faktor Arbeit durch größeren Kapitaleinsatz substituiert wurde^[11] (wie bei der Automatisierung) und umgekehrt.

Die Addition von verschiedenen Kapitalarten zu einem Gesamtkapitalstock beruht auf zweifelhaften Annahmen, die im Zuge der Kapitalkontroverse kritisiert wurden.

Empirische Befunde

OECD-Wirtschaftsdaten grafisch dargestellt

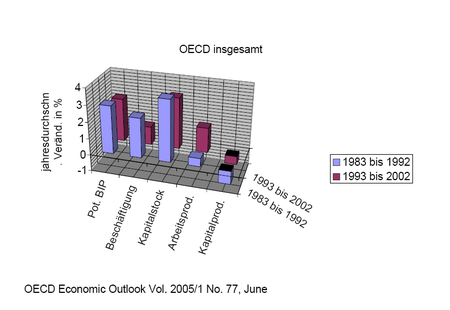
Laut OECD^[12] ist in den OECD-Ländern, also in etwa den Industriestaaten, die potenzielle Produktion (Produktion bei normaler Auslastung des Kapitalstocks) jahresdurchschnittlich von 1983 bis 1992 um 2,9 % gestiegen. Dieses verlangsamte sich etwas auf jahresdurchschnittlich 2,6 % 1993 bis 2002. Die Beschäftigung wuchs in diesen angegebenen Zeiträumen jahresdurchschnittlich 2,4 % und 1,1 %. Der Beschäftigungszuwachs hat sich also in der OECD verlangsamt.

Für die Arbeitsproduktivität ergibt sich daraus ungefähr ein Wachstum von 0,5 % im ersten und 1,5 % im zweiten Zeitabschnitt. Das Arbeitsproduktivitätswachstum hat sich demnach beschleunigt. Der Kapitalstock wuchs um 3,7 % bzw. um 3,1 % jahresdurchschnittlich, also rascher als die Produktion. Die Kapitalproduktivität hat sich demnach vermindert, jahresdurchschnittlich um 0,8 % 1983 bis 1993 und um 0,5 % 1993 bis 2002.

In aller Regel nimmt die Arbeitsproduktivität mittel- und langfristig zu, während die Kapitalproduktivität eher sinkt wie hier in den OECD-Ländern. Eine bemerkenswerte Ausnahme sind die USA, für welche die OECD ein Wachstum der Kapitalproduktivität 1983 bis 1992 von jahresdurchschnittlich 0,1 % und von 1993 bis 2002 von ebenfalls 0,1 % angibt.

Eine langfristig sinkende Kapitalproduktivität ist problematisch, da dies bedeutet, dass langfristig die gesamtwirtschaftliche Kapitalrentabilität (Kapitalertrag im Verhältnis zum Kapitalstock) nur gehalten werden kann, wenn der Anteil der Arbeitseinkommen am BIP verkleinert wird, wobei dieses spätestens dann ein Ende hätte, wenn die Lohnquote den Wert null erreicht hätte.

Totale Faktorproduktivität

Die totale Faktorproduktivität (englisch total factor productivity) berücksichtigt das Zusammenwirken aller Produktionsfaktoren.^[13] Sie zeigt das Verhältnis der Ausbringung zu allen eingesetzten Produktionsfaktoren an und gibt bei der Analyse des Wirtschaftswachstums Auskunft darüber, inwieweit technischer Fortschritt eine höhere Ausbringung bei gleichem Faktoreinsatz ermöglicht. Bei der Berechnung wird eine konstante Kapazitätsauslastung unterstellt.

Die totale Faktorproduktivität $TFP$ ergibt sich aus der Gegenüberstellung der Ausbringungsmenge $Am$ und sämtlicher Faktorkosten $FK$ .^[14]

TFP={\frac {Am}{FK}}

.

Die Produktionsfunktion berücksichtigt bei der totalen Faktorproduktivität das vorhandene Technologieniveau $A$ , so dass sich die Ausbringung (output) nicht nur wegen einer Vermehrung von Arbeit ( $L$ ) und Kapital ( $K$ ), sondern auch wegen einer Verbesserung der Technologie erhöht:^[15]

Y=AF(K,L)

.

Bei einem Mehrproduktunternehmen müssen zur Erfassung seiner Gesamtproduktivität alle Inputs ins Verhältnis zu allen Outputs gesetzt werden^[16] und sämtliche Produktgruppen des gesamten Produktionsprogramms erfassen.

Empirisch lässt sich beobachten, dass das Wachstum des Outputs $Y$ sich nicht nur aus dem Wachstum der Inputs Arbeit $L$ und Kapital $K$ erklären lässt, sondern dass sozusagen ein unerklärlicher Rest übrig bleibt. Dieser Teil der Wachstumsrate von $Y$ , der nicht durch Veränderungen in den Einsatzmengen von $L$ oder $K$ erklärt werden kann, wird als totale Faktorproduktivität bezeichnet. Sie kann als Maß für den technischen Fortschritt gedeutet werden, der unabhängig vom Einsatz der Produktionsfaktoren für ein Wachstum des Outputs $Y$ sorgt.

Empirische Befunde

In einer Studie wurde die Bedeutung von verschiedenen Standortfaktoren für die totale Faktorproduktivität einer Region untersucht anhand der Daten von 257 Regionen der EU.^[17] Für die Analyse wurden potentiell beeinflussende Eigenschaften der Regionen berücksichtigt wie z. B. der Spezialisierungsgrad im Bereich verarbeitendes Gewerbe, Siedlungsstruktur, Populationsdichte und das wirtschaftliche Entwicklungsniveau der Region. Den stärksten positiven Einfluss auf die totale Faktorproduktivität einer Region hatten (in absteigender Reihenfolge):

der Anteil der Berufstätigen mit Studienabschluss in kreativen Berufsfeldern (z. B. Natur- und Sozialwissenschaften, Life Science und Gesundheit, Lehrer, Ingenieurwesen …),
die Anzahl der angemeldeten Patente je tausend Einwohner (als Maß für das technologische Kapital) und
die kulturelle Diversität.

Einen negativen Einfluss hatten der Spezialisierungsgrad des verarbeitenden Gewerbes und die Jahresdurchschnittstemperatur.

Grenzproduktivität

Volks- und betriebswirtschaftlich interessant ist neben der bisher betrachteten Durchschnittsproduktivität der Faktoren auch ihre Grenzproduktivität:

{\frac {\partial x}{\partial r_{i}}}

Diese gibt an, um wie viel sich der Output erhöht, wenn der Faktoreinsatz um eine Einheit steigt, bei Konstanz der anderen Faktoren. Die Grenzproduktivität des Faktors Arbeit kann z. B. daran gemessen werden, um welchen Betrag der Output wächst, wenn eine zusätzliche Arbeitsstunde geleistet wird. Grenzproduktivitäten sind von besonderem Interesse, weil sie – laut Theorie – auf vollkommenen Faktormärkten den Marktpreis für den Faktor bestimmen. In der Regel nach der Wertgrenzproduktivität: ${\text{WGP}}={\text{Grenzproduktivität}}\cdot {\text{Outputpreis}}$ . Im Optimum gilt, dass das WGP dem Faktorpreis (zur Ermittlung der Optimalen Faktoreinsatzmenge) entspricht.

In den meisten Fällen geht man von einer positiven, aber abnehmenden Grenzproduktivität aus, d. h. bei einer Erhöhung des Inputs wird der Output ansteigen. Die Höhe des Anstiegs wird aber mit steigendem Ausgangsniveau des Inputs geringer (vgl. Ertragsgesetz).

Mathematisch kann die Grenzproduktivität eines Faktors als partielle Ableitung der Produktionsfunktion nach diesem Faktor ermittelt werden.

Siehe auch

Weblinks

Wikiquote: Produktivität – Zitate

Andreas Dikow: Marktorientiertes Konzept zum Produktivitätsmanagement in produzierenden Unternehmen. (PDF; 1,12 MB)
Produktivität – Schweizer Bundesamt für Statistik, 2020
Wohlstand durch Produktivität – Deutschland im internationalen Vergleich (PDF; 331 kB) – Expertisen und Dokumentationen zur Wirtschafts- und Sozialpolitik. Friedrich-Ebert-Stiftung, März 2009

Einzelnachweise

↑ Helmut Weber, Rentabilität, Produktivität und Liquidität: Größen zur Beurteilung und Steuerung von Unternehmen, 1998, S. 87
↑ Hans Corsten, Produktionswirtschaft, 6. Auflage, 1996, S. 46 f.
↑ REFA – Methodenlehre des Arbeitsstudiums, Teil 1 „Grundlagen“. Carl Hanser, München, 1971, ISBN 3-446-14234-7, S. 43 ff.
↑ Eggert Winter/Katrin Alisch/Ute Arentzen, Gabler Wirtschaftslexikon, 2004, S. 1018
↑ Gottfried Bombach, Probleme der Produktivitätsmessung, in: Konjunkturpolitik, 1959, S. 322
↑ Horst Penzkofer/Heinz Schmalholz/Lothar Scholz, Innovation, Wachstum und Beschäftigung, 1989, S. 100; ISBN 9783110119879
↑ Helmut Weber, Rentabilität, Produktivität und Liquidität: Größen zur Beurteilung und Steuerung von Unternehmen, 1998, S. 89 f.
↑ Verlag der Sozialistischen Monatshefte (Hrsg.), Sozialistische Monatshefte, Band 1, 1919, S. 25
↑ BWL-Lexikon.de, Bodenproduktivität
↑ Reinhold Sellien/Helmut Sellien, Gablers Wirtschafts-Lexikon, Band 1, 1988, Sp. 2763
↑ Dieter Brümmerhoff/Heinrich Lützel, Lexikon der Volkswirtschaftlichen Gesamtrechnungen, 2002, S. 216
↑ OECD (Hrsg.), Economic Outlook No. 77, Juni 2005
↑ Horst Albach/Margareta Kulessa, Produktivität, in: Günter Renz/Johannes Eurich/Jörg Hübner/Margareta Kulessa/Martin Honecker/Traugott Jähnichen (Hrsg.), Evangelisches Soziallexikon, 2016, o. S.
↑ Charles T. Horngren/George Foster/Srikant M. Datar, Kostenrechnung: Entscheidungsorientierte Perspektive, 2001, S. 827
↑ N. Gregory Mankiw, Makroökonomik, 2017, S. 329 f.
↑ Frank Schulz-Nieswandt/Holger Mühlenkamp/Ludwig Theuvsen/Markus Krajewski (Hrsg.), Öffentliche Wirtschaft, 2019, S. 346
↑ Emanuela Marrocu/Raffaele Paci: Education or Creativity: What Matters Most for Economic Performance? In: Economic Geography. Band 88, Nr. 4, Oktober 2012, S. 369–401, doi:10.1111/j.1944-8287.2012.01161.x (wiley.com [abgerufen am 19. Juni 2019]).

[1] Helmut Weber, Rentabilität, Produktivität und Liquidität: Größen zur Beurteilung und Steuerung von Unternehmen, 1998, S. 87

[2] Hans Corsten, Produktionswirtschaft, 6. Auflage, 1996, S. 46 f.

[REFA-1-3] REFA – Methodenlehre des Arbeitsstudiums, Teil 1 „Grundlagen“. Carl Hanser, München, 1971, ISBN 3-446-14234-7, S. 43 ff.

[4] Eggert Winter/Katrin Alisch/Ute Arentzen, Gabler Wirtschaftslexikon, 2004, S. 1018

[5] Gottfried Bombach, Probleme der Produktivitätsmessung, in: Konjunkturpolitik, 1959, S. 322

[6] Horst Penzkofer/Heinz Schmalholz/Lothar Scholz, Innovation, Wachstum und Beschäftigung, 1989, S. 100; ISBN 9783110119879

[7] Helmut Weber, Rentabilität, Produktivität und Liquidität: Größen zur Beurteilung und Steuerung von Unternehmen, 1998, S. 89 f.

[8] Verlag der Sozialistischen Monatshefte (Hrsg.), Sozialistische Monatshefte, Band 1, 1919, S. 25

[9] BWL-Lexikon.de, Bodenproduktivität

[10] Reinhold Sellien/Helmut Sellien, Gablers Wirtschafts-Lexikon, Band 1, 1988, Sp. 2763

[11] Dieter Brümmerhoff/Heinrich Lützel, Lexikon der Volkswirtschaftlichen Gesamtrechnungen, 2002, S. 216

[12] OECD (Hrsg.), Economic Outlook No. 77, Juni 2005

[13] Horst Albach/Margareta Kulessa, Produktivität, in: Günter Renz/Johannes Eurich/Jörg Hübner/Margareta Kulessa/Martin Honecker/Traugott Jähnichen (Hrsg.), Evangelisches Soziallexikon, 2016, o. S.

[14] Charles T. Horngren/George Foster/Srikant M. Datar, Kostenrechnung: Entscheidungsorientierte Perspektive, 2001, S. 827

[15] N. Gregory Mankiw, Makroökonomik, 2017, S. 329 f.

[16] Frank Schulz-Nieswandt/Holger Mühlenkamp/Ludwig Theuvsen/Markus Krajewski (Hrsg.), Öffentliche Wirtschaft, 2019, S. 346

[17] Emanuela Marrocu/Raffaele Paci: Education or Creativity: What Matters Most for Economic Performance? In: Economic Geography. Band 88, Nr. 4, Oktober 2012, S. 369–401, doi:10.1111/j.1944-8287.2012.01161.x (wiley.com [abgerufen am 19. Juni 2019]).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]