Die Quadratsummen-Funktion (engl. sum of squares function )
r
k
(
n
)
{\displaystyle r_{k}(n)}
zahlentheoretische Funktion , die angibt, auf wie viele Arten eine gegebene natürliche Zahl
n
{\displaystyle n}
k
{\displaystyle k}
ganzer Zahlen dargestellt werden kann, wobei alle Vertauschungen und Vorzeichenkombinationen mitgezählt werden.
Die ersten Werte von rk (Primzahlen mit hellblauen Hintergrund)
n
n
r1 (n)
r2 (n)
r3 (n)
r4 (n)
r5 (n)
r6 (n)
r7 (n)
r8 (n)
0
0
1
1
1
1
1
1
1
1
1
1
2
4
6
8
10
12
14
16
2
2
0
4
12
24
40
60
84
112
3
3
0
0
8
32
80
160
280
448
4
22
2
4
6
24
90
252
574
1136
5
5
0
8
24
48
112
312
840
2016
6
2‧3
0
0
24
96
240
544
1288
3136
7
7
0
0
0
64
320
960
2368
5504
8
23
0
4
12
24
200
1020
3444
9328
9
32
2
4
30
104
250
876
3542
12112
10
2‧5
0
8
24
144
560
1560
4424
14112
11
11
0
0
24
96
560
2400
7560
21312
12
22 ‧3
0
0
8
96
400
2080
9240
31808
13
13
0
8
24
112
560
2040
8456
35168
14
2‧7
0
0
48
192
800
3264
11088
38528
15
3‧5
0
0
0
192
960
4160
16576
56448
16
24
2
4
6
24
730
4092
18494
74864
17
17
0
8
48
144
480
3480
17808
78624
18
2‧32
0
4
36
312
1240
4380
19740
84784
19
19
0
0
24
160
1520
7200
27720
109760
20
22 ‧5
0
8
24
144
752
6552
34440
143136
Die Funktion ist für alle
n
∈
N
≥
0
{\displaystyle n\in \mathbb {N} _{\geq 0}}
k
∈
N
≥
1
{\displaystyle k\in \mathbb {N} _{\geq 1}}
[ 1]
r
k
(
n
)
:=
∑
a
1
2
+
a
2
2
+
⋯
+
a
k
2
=
n
(
a
1
,
a
2
,
…
,
a
k
)
∈
Z
k
1
=
|
{
(
a
1
,
a
2
,
…
,
a
k
)
∈
Z
k
∣
a
1
2
+
a
2
2
+
⋯
+
a
k
2
=
n
}
|
,
{\displaystyle r_{k}(n):=\sum _{\begin{array}{c}a_{1}^{2}+a_{2}^{2}+\cdots +a_{k}^{2}=n\\(a_{1},a_{2},\dots ,a_{k})\in \mathbb {Z} ^{k}\end{array}}1={\big |}\left\{(a_{1},a_{2},\dots ,a_{k})\in \mathbb {Z} ^{k}\mid a_{1}^{2}+a_{2}^{2}+\cdots +a_{k}^{2}=n\right\}{\big |},}
d. h. als Anzahl der Darstellungsmöglichkeiten von
n
{\displaystyle n}
k
{\displaystyle k}
k
≥
1
{\displaystyle k\geq 1}
r
2
{\displaystyle r_{2}}
r
{\displaystyle r}
r
k
(
0
)
=
1
{\displaystyle r_{k}(0)=1}
für alle
k
{\displaystyle k}
r
2
(
1
)
=
4
{\displaystyle r_{2}(1)=4}
da
1
=
0
2
+
(
±
1
)
2
=
(
±
1
)
2
+
0
2
{\displaystyle 1=0^{2}+(\pm 1)^{2}=(\pm 1)^{2}+0^{2}}
r
2
(
2
)
=
4
{\displaystyle r_{2}(2)=4}
wegen
2
=
(
±
1
)
2
+
(
±
1
)
2
{\displaystyle 2=(\pm 1)^{2}+(\pm 1)^{2}}
r
2
(
3
)
=
0
{\displaystyle r_{2}(3)=0}
weil es keine Darstellung der Zahl 3 als Summe von 2 Quadraten gibt.
Aus der Definition folgt sofort die Beziehung
r
k
+
m
(
n
)
=
∑
t
=
0
n
r
k
(
t
)
r
m
(
n
−
t
)
,
{\displaystyle r_{k+m}(n)=\sum _{t=0}^{n}r_{k}(t)\ r_{m}(n-t),}
aus der sich eine Rekursionsformel zur effizienten Berechnung ableiten lässt:
r
k
+
1
(
n
)
=
r
k
(
n
)
+
2
∑
t
=
1
n
r
k
(
n
−
t
2
)
.
{\displaystyle r_{k+1}(n)=r_{k}(n)+2\sum _{t=1}^{\sqrt {n}}r_{k}(n-t^{2}).}
Es sei[ 2]
R
k
(
x
)
:=
∑
n
=
0
x
r
k
(
n
)
=
∑
a
1
2
+
a
2
2
+
⋯
+
a
k
2
≤
x
1
{\displaystyle R_{k}(x):=\sum _{n=0}^{x}r_{k}(n)=\sum _{a_{1}^{2}+a_{2}^{2}+\dotsb +a_{k}^{2}\leq x}1}
Das ist anschaulich die Anzahl der (ganzzahligen) Gitterpunkte in einer
k
{\displaystyle k}
x
{\displaystyle {\sqrt {x}}}
R
k
(
x
)
=
V
k
x
k
2
+
O
(
x
k
−
1
2
)
{\displaystyle R_{k}(x)=V_{k}x^{\frac {k}{2}}+O(x^{\frac {k-1}{2}})}
wobei
O
(
.
)
{\displaystyle O(.)}
Landau-Symbol ist und die Konstanten
V
k
{\displaystyle V_{k}}
k
{\displaystyle k}
V
2
=
π
,
V
3
=
4
3
π
,
V
4
=
1
2
π
2
,
…
{\displaystyle V_{2}=\pi ,\;V_{3}={\frac {4}{3}}\pi ,\;V_{4}={\frac {1}{2}}\pi ^{2},\;\dots }
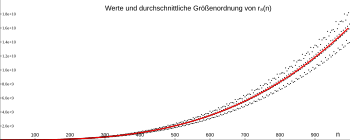
Die durchschnittliche Größenordnung von
r
k
(
n
)
{\displaystyle r_{k}(n)}
k
2
V
k
x
k
2
−
1
{\displaystyle {\tfrac {k}{2}}V_{k}x^{{\tfrac {k}{2}}-1}}
π
{\displaystyle \pi }
r
2
(
x
)
{\displaystyle r_{2}(x)}
Die erzeugende Funktion erhält man als Potenz der Jacobischen Thetafunktion
ϑ
(
z
,
q
)
{\displaystyle \vartheta (z,q)}
z
=
0
{\displaystyle z=0}
[ 3]
ϑ
3
(
q
)
:=
ϑ
(
0
,
q
)
=
∑
n
=
−
∞
∞
q
n
2
=
1
+
2
q
+
2
q
4
+
2
q
9
+
2
q
16
+
⋯
{\displaystyle \vartheta _{3}(q):=\vartheta (0,q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}=1+2q+2q^{4}+2q^{9}+2q^{16}+\dotsb }
Man erhält daraus
(
ϑ
3
(
q
)
)
k
=
∑
n
1
,
n
2
,
…
,
n
k
q
n
1
2
+
n
2
2
+
⋯
+
n
k
2
=
∑
n
=
0
∞
q
n
∑
n
1
2
+
n
2
2
+
⋯
+
n
k
2
=
n
1
=
∑
n
=
0
∞
q
n
r
k
(
n
)
{\displaystyle (\vartheta _{3}(q))^{k}=\sum _{n_{1},n_{2},\dotsc ,n_{k}}q^{n_{1}^{2}+n_{2}^{2}+\dotsb +n_{k}^{2}}=\sum _{n=0}^{\infty }q^{n}\sum _{n_{1}^{2}+n_{2}^{2}+\dotsb +n_{k}^{2}=n}1=\sum _{n=0}^{\infty }q^{n}\ r_{k}(n)}
Werte und durchschnittliche Größenordnung von r2 (n) Werte und durchschnittliche Größenordnung von r4 (n) Werte und durchschnittliche Größenordnung von r8 (n) Einige spezielle Formeln sind z. B. (für
n
>
0
{\displaystyle n>0}
Für
k
=
2
{\displaystyle k=2}
r
2
(
n
)
=
4
∑
d
∣
n
d
≡
1
(
mod
2
)
(
−
1
)
(
d
−
1
)
/
2
{\displaystyle r_{2}(n)=4\sum _{d\mid n \atop d\equiv 1{\pmod {2}}}(-1)^{(d-1)/2}}
Mit Hilfe der Primfaktorzerlegung
n
=
2
g
p
1
f
1
p
2
f
2
⋯
q
1
h
1
q
2
h
2
⋯
{\displaystyle n=2^{g}p_{1}^{f_{1}}p_{2}^{f_{2}}\cdots q_{1}^{h_{1}}q_{2}^{h_{2}}\cdots }
p
i
{\displaystyle p_{i}}
p
i
≡
1
(
mod
4
)
{\displaystyle p_{i}\equiv 1{\pmod {4}}}
q
i
{\displaystyle q_{i}}
q
i
≡
3
(
mod
4
)
{\displaystyle q_{i}\equiv 3{\pmod {4}}}
r
2
(
n
)
=
4
(
f
1
+
1
)
(
f
2
+
1
)
⋯
{\displaystyle r_{2}(n)=4(f_{1}+1)(f_{2}+1)\cdots }
wenn alle Exponenten
h
1
,
h
2
,
…
{\displaystyle h_{1},h_{2},\dotsc }
h
i
{\displaystyle h_{i}}
r
2
(
n
)
=
0
{\displaystyle r_{2}(n)=0}
r
2
(
n
)
{\displaystyle r_{2}(n)}
Gaußschen Zahlen mit der Norm
n
{\displaystyle n}
Für
k
=
3
{\displaystyle k=3}
quadratfreie Zahlen
n
>
4
{\displaystyle n>4}
r
3
(
n
)
=
{
24
h
(
−
n
)
,
wenn
n
≡
3
(
mod
8
)
,
0
wenn
n
≡
7
(
mod
8
)
,
12
h
(
−
4
n
)
sonst
,
{\displaystyle r_{3}(n)={\begin{cases}24h(-n),&{\text{wenn }}n\equiv 3{\pmod {8}},\\0&{\text{wenn }}n\equiv 7{\pmod {8}},\\12h(-4n)&{\text{sonst}},\end{cases}}}
wobei
h
(
m
)
{\displaystyle h(m)}
Klassenzahl einer ganzen Zahl
m
{\displaystyle m}
Für beliebige
n
>
0
{\displaystyle n>0}
Drei-Quadrate-Satz
r
3
(
n
)
=
0
{\displaystyle r_{3}(n)=0}
n
{\displaystyle n}
n
=
4
a
(
8
b
+
7
)
,
a
≥
0
,
b
≥
0
{\displaystyle n=4^{a}(8b+7),a\geq 0,b\geq 0}
[ 4]
Die Formel für
k
=
4
{\displaystyle k=4}
Carl Gustav Jacob Jacobi und liefert
r
4
(
n
)
{\displaystyle r_{4}(n)}
n
,
{\displaystyle n,}
Satz von Jacobi ):
r
4
(
n
)
=
8
∑
d
∣
n
;
4
∤
d
d
{\displaystyle r_{4}(n)=8\sum _{d\mid n;4\nmid d}d}
Für alle Primzahlen
p
{\displaystyle p}
r
4
(
p
)
=
8
(
p
+
1
)
{\displaystyle r_{4}(p)=8(p+1)}
r
4
(
2
k
)
=
24
,
k
≥
1
{\displaystyle r_{4}(2^{k})=24,\;k\geq 1}
r
4
(
n
)
{\displaystyle r_{4}(n)}
Lipschitz-Quaternionen mit der Norm
n
{\displaystyle n}
Für die Anzahl der Darstellungen von
n
{\displaystyle n}
2
s
{\displaystyle 2s}
s
≥
3
{\displaystyle s\geq 3}
r
6
(
n
)
=
16
∑
d
∣
n
χ
(
n
d
)
d
2
−
4
∑
d
∣
n
χ
(
d
)
d
2
=
4
∑
d
∣
n
[
4
χ
(
n
d
)
−
χ
(
d
)
]
d
2
{\displaystyle r_{6}(n)=16\sum _{d\mid n}\chi ({\tfrac {n}{d}})d^{2}-4\sum _{d\mid n}\chi (d)d^{2}=4\sum _{d\mid n}[4\chi ({\tfrac {n}{d}})-\chi (d)]d^{2}}
wobei
χ
(
d
)
=
+
1
,
−
1
,
0
{\displaystyle \chi (d)=+1,-1,0}
d
{\displaystyle d}
4
k
+
1
,
4
k
−
1
,
2
k
{\displaystyle 4k+1,4k-1,2k}
[ 5]
Jacobi fand auch eine explizite Formel für
k
=
8
{\displaystyle k=8}
r
8
(
n
)
=
16
∑
d
∣
n
(
−
1
)
n
+
d
d
3
{\displaystyle r_{8}(n)=16\sum _{d\mid n}(-1)^{n+d}d^{3}}
Der Limes
K
:=
lim
n
→
∞
(
∑
k
=
1
n
r
2
(
k
)
k
−
π
log
n
)
{\displaystyle K:=\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {r_{2}(k)}{k}}-\pi \log n\right)}
existiert und wird (nach Wacław Sierpiński ) als Sierpiński-Konstante bezeichnet. Diese lässt sich durch die Kreiszahl , die Euler-Mascheroni-Konstante und die Gammafunktion ausdrücken:
K
=
π
(
2
γ
+
4
log
Γ
(
3
4
)
−
log
π
)
{\displaystyle K=\pi (2\gamma +4\log \Gamma ({\tfrac {3}{4}})-\log \pi )}
↑ E. Krätzel: Zahlentheorie . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, S. 165 .
↑ E. Krätzel: Zahlentheorie . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, S. 197 .
↑ Godfrey Harold Hardy , E. M. Wright: Einführung in die Zahlentheorie . R. Oldenbourg, München 1958, S. 294, 353 . ↑ E. Krätzel: Zahlentheorie . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, S. 162 .
↑ Godfrey Harold Hardy , E. M. Wright: Einführung in die Zahlentheorie . R. Oldenbourg, München 1958, S. 357 . 




























































![{\displaystyle r_{6}(n)=16\sum _{d\mid n}\chi ({\tfrac {n}{d}})d^{2}-4\sum _{d\mid n}\chi (d)d^{2}=4\sum _{d\mid n}[4\chi ({\tfrac {n}{d}})-\chi (d)]d^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c5f393d58fe3e854b9facab8e5f02c9add19f2)






