Quandle
Zur Navigation springen
Zur Suche springen
Ein Quandle ist in der Mathematik eine algebraische Struktur, die vor allem in der Knotentheorie Anwendung findet.
Definition
[Bearbeiten | Quelltext bearbeiten]Ein Quandle ist eine Menge mit einer Operation , so dass für alle gilt:
- (i)
- (ii) die durch definierte Abbildung ist eine Bijektion
- (iii) .
Bedingung (iii) heißt Selbstdistributivität.
Weil eine Bijektion ist, gibt es eine inverse Abbildung . Die Operation wird für durch
definiert.
Reidemeister-Bewegungen
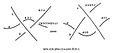
[Bearbeiten | Quelltext bearbeiten]Die Quandle-Operationen lassen sich mittels der Reidemeister-Bewegungen von Knotendiagrammen interpretieren:
-
Reidemeister I
-
Reidemeister II
-
Reidemeister III
Beispiele
[Bearbeiten | Quelltext bearbeiten]- Jede abelsche Gruppe ist ein Quandle mit der Operation
- .
- Für eine Gruppe und definiert man den Quandle als die Menge mit der Operation
- .
- Für eine Gruppe definiert man den Quandle als die Menge mit der Operation
- .
- Jeder -Modul ist ein Quandle mit der Operation
- .
- Diese Quandle werden als Alexander-Quandle bezeichnet.
- Der Fundamentalquandle eines Knotens (oder allgemeiner einer Verschlingung) ist definiert wie folgt. Sei das Komplement einer regulären Umgebung und . Definiere
- mit der (wohldefinierten) Verknüpfung
- ,
- wobei den Meridian durch bezeichnet.
Literatur
[Bearbeiten | Quelltext bearbeiten]- David Joyce: A classifying invariant of knots, the knot quandle. J. Pure Appl. Algebra 23 (1982), no. 1, 37–65.
- Sergei Matwejew: Distributive groupoids in knot theory. (russisch) Mat. Sb. (N.S.) 119(161) (1982), no. 1, 78–88, 160.





















![{\displaystyle \mathbb {Z} \left[t^{\pm 1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ffa18b92d23581bf13760d359ba59a19b380ab2)





![{\displaystyle \left[\gamma _{1}\right]\triangleright \left[\gamma _{2}\right]=\left[\gamma _{2}\circ m_{\gamma _{2}(1)}\circ \gamma _{2}^{-1}\circ \gamma _{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47118ae4c59443498e10442ef7757367017cf2a9)

