Ewiger Kalender

Der Ewige Kalender ist eine Tabelle bzw. eine Übersicht, die innerhalb eines gewählten Zeitraums die Wochentagsbezeichnung einem Kalenderdatum zuordnet und bei der sich für ein beliebiges Jahr der zu einem Datum gehörende Wochentag ablesen lässt. „Wie ist der Wochentag welchen Datums“ lässt sich hier ohne Weiteres wegen der Folge des 1. Januars nachvollziehen. Dabei stehen die Daten der Monate Januar und Februar in der ersten Zeile, die der Monate März bis Dezember in der zweiten Zeile. Bisherige sogenannte Ewige Kalender/Dauerkalender/Immerwährende... stellen lediglich Ermittlungsvorschriften dar. Mangels einer besseren Lösung wurde der Name jahrhundertelang vergeben.

Außer der Anzeige des Wochentags sowie der Feiertage kann ein Kalender für den täglichen Gebrauch auch noch etliche Informationen mehr enthalten; im Folgenden wird allerdings nur der Basiskalender – also die Grundstruktur – behandelt.

Ewiger Gregorianischer Kalender

In welchem Jahr tritt eine Deckungsgleichheit ein? Im Schaltjahr 2020 ist der 1. Januar ein Mittwoch; in welchem Schaltjahr ist der 1. Januar wieder ein Mittwoch? Die Lösung ist durch Nutzung der vorliegenden Daten gegeben.

Vom Basis-Schaltjahr-Wochentag sind fünf Wochentage zu addieren bzw. zwei Wochentage zu subtrahieren, um zum nächstfolgenden Schaltjahr zu gelangen. Demnach ist der Wochentag des 1. Januar: 2020 Mittwoch, 2024 Montag, 2028 Samstag, 2032 Donnerstag, 2036 Dienstag, 2040 Sonntag, 2044 Freitag, 2048 Mittwoch.

2020 entspricht dem Jahr 2048. Die Erkenntnis ist damit folgerichtig: Ein Basiskalender ist immer nach 28 Jahren wieder verwendbar. Die jeweiligen Gemeinjahre dazwischen wiederholen sich gleichfalls alle 28 Jahre. Die bekannte Deckungsgleichheit wird am Beispiel des hier begangenen Weges sichtbar.

Ein Kalender für größere Zeiträume wird dargestellt, indem zunächst ein Kalender für 28 Jahre nach obigem Muster gebildet wird. Dieser ist identisch bezüglich der Wochentagsfolge der folgenden 28 Jahre (Kleiner Zyklus: 7 Wochentage × 4 Jahre Schalttagsrhythmus). Dieser Vorgang wird wiederholt, bis der gewünschte Zeitrahmen erreicht ist. Mit welchem Jahr begonnen wird, ist dabei frei wählbar. Bekannt ist das „Weiterrücken“ der Jahre - der erste Januar - um einen Tag bzw. um zwei Tage nach einem Schaltjahr. Dies ergibt sich bei Division von 365 Tagen/Gemeinjahr dividiert durch 7 Tage/Woche = XY, mit Rest 1 Tag. Damit ist klar: ein Gemeinjahr endet immer mit dem Wochentag des ersten Januars, ein Schaltjahr demnach mit dem Folgewochentag. Das Ergebnis der Division XY = 52 Wochen hat keinerlei Bedeutung hinsichtlich der Kalenderwoche.

Papst Gregor XIII. bestimmte u. a. im Prinzip, dass auf Donnerstag, den 4. Oktober 1582^jul. unmittelbar Freitag, der 15. Oktober 1582^greg. als Beginn der neuen Kalenderrechnung zu folgen hatte und nur die Jahrhundert-Jahreskalender einen Schalttag haben dürfen, wenn deren volle Jahreszahlen durch 400 (ohne Rest) teilbar sind. Die Gemeinjahreskalender werden für die Jahre 1700/1800/1900 in den ewigen Gregorianischen Kalenderentwurf eingeordnet.

Für die Jahre, welche dem jeweiligen Jahrhundert-Jahreskalender folgen, ist zu beachten, dass es jeweils ein Jahreskalender ist, welcher drei Jahre vor einem Schaltjahr steht, um oben genannter Tatsache - Weiterrücken des 1. Januar - gerecht zu werden und in den Schalttagsrhythmus zu gelangen.

Nach dem Aufbau eines Ewigen gregorianischen Kalenders wird festgestellt, die Folge der Jahreskalender wiederholt sich deckungsgleich nach 400 Jahren. Dementsprechend sind die jeweiligen Blöcke in der Darstellung ab 1600 übereinander gelegt.

Ewiger Julianischer und Gregorianischer Kalender

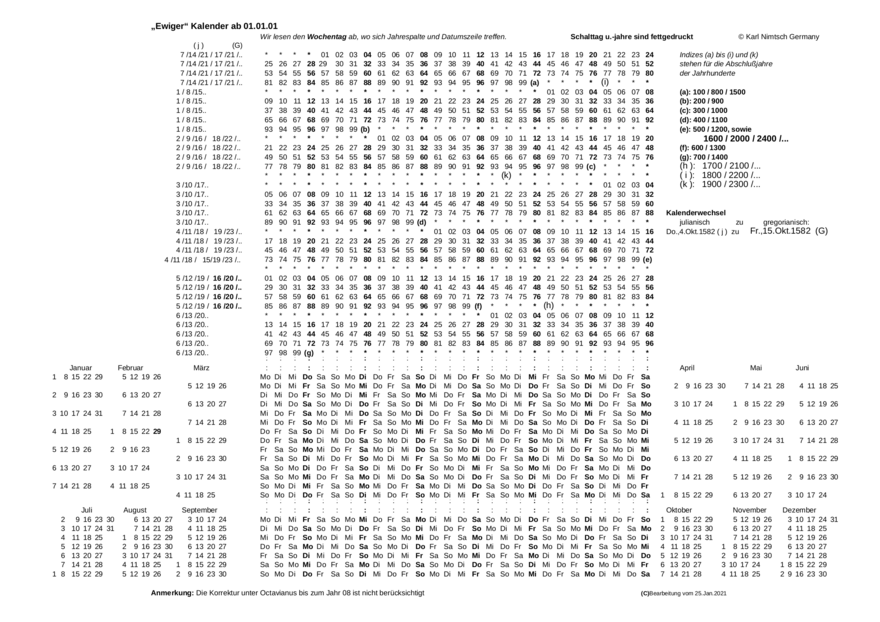
Die Kalenderdarstellungen julianisch und gregorianisch sind in einem Exemplar zusammengefasst dargestellt. Dabei wird von der Deckungsgleichheit der Jahre 1600^jul. / 2000^jul. mit den Jahren 1600^greg. / 2000^greg. ausgegangen, und die Daten dementsprechend eingeordnet.

Man beginnt den Aufbau des Ewigen Julianischen Kalenders, indem die vordem beschriebene Zuordnung mit dem 1. Januar des Jahres 1 nach Christus zum Wochentag „Sa“ und ordnet diese Jahresspalte „01“ einer Jahresspalte des Monats- und Wochentagsblockes – übernommen vom Gregorianischen Kalender – zu, in welcher der Wochentag „Sa“ drei Jahre vor einem Schaltjahr steht (da das Jahr 4 n. Chr. ein Schaltjahr sein muss). Nun werden die Folgejahre der Reihe nach den Wochentagsspalten – wie vor – zugeordnet bis zum Jahr am rechten Rand. Sind 28 Spalten belegt, wird mit der nächsten Jahresspalte links von vorn begonnen usw. usf. bis der erste Block vom Jahr 1 n. Chr. bis zum Jahr 100 n. Chr. (ein Schaltjahr) aufgefüllt ist.

Um die Einzeljahre bzw. deren Blöcke den Jahrhunderten anschaulich zuordnen zu können, ist eine Leerzeile eingefügt. Nach Erstellung des 7. Blockes wird mit dem zum 1. Jahrhundert deckungsgleichen Block des 8. Jahrhunderts begonnen und der 700-Jahre-Wiederholturnus des Julianischen Kalenders dargestellt.

Wiederkehr der Jahreskalender

Die Erkenntnisse von Butkewitsch können den ewigen Kalendern entnommen werden.^[1] Ein Gemein-Jahreskalender ist mit dem deckungsgleich, welcher mit demselben Wochentag beginnt, sinngemäß des Schaltjahreskalenders.

Regelfall

Sind wir im Gemeinjahr 1 Jahr nach / 3 Jahre vor dem Schaltjahr, dann wiederholt sich jenes in 6 Jahren, nach weiteren 11 Jahren und nach weitern 11 Jahren bis der Zyklus wieder von vorne beginnt.
Sind wir im Gemeinjahr 2 Jahre nach / 2 Jahre vor dem Schaltjahr, dann wiederholt sich jenes in 11 Jahren, nach weiteren 6 Jahren und nach weitern 11 Jahren bis der Zyklus wieder von vorne beginnt.
Sind wir im Gemeinjahr 3 Jahre nach / 1 Jahr vor dem Schaltjahr, dann wiederholt sich jenes in 11 Jahren, nach weiteren 11 Jahren und nach weitern 6 Jahren bis der Zyklus wieder von vorne beginnt.
Sind wir im Schaltjahr, dann wiederholt sich jenes aller 28 Jahre.

Ausnahmen

Jahrhundertwechsel-Ausnahme

In einem Jahrhundert-Jahr wie zum Beispiel 1700, 1800 oder 1900 entfällt das Schaltjahr.

Dadurch repetiert sich ein Gemeinjahr erst ein Jahr später, also in 12 Jahren. Dieser Fall gilt die Gemeinjahre x90−y02 , x91−y03 , x97−y09 und x98−y10. (4 von 7 Wochentagszuordnungen)

Eine Wiederholung nach 7 Jahren ist nicht möglich, weil dafür mindestens 8 Gemeinjahre in Folge auftreten müssten, was nie der Fall ist.

Möglich wird durch den Ausfall des Schalttages aber auch eine zweimalige Wiederholung der Gemeinjahre nach jeweils 6 Jahren. Dies trifft für die Gemeinjahre x93−x99−y05 , x94−y00−y06 und x95−y01−y07 zu. (3 von 7 Wochentagszuordnungen)

Ein Schaltjahr repetiert sich nach 12 Jahren falls es 4 oder 8 Jahre vor dem Jahrhundert-Jahr liegt, sonst erst nach 40 Jahren.

Vier-Jahrhundertwechsel-Egalisierung

Über einen Vier-Jahrhundertwechsel hinweg, also zum Beispiel 1600, 2000 oder 2400, wird die vorherige Jahrhundertwechsel-Ausnahme-Regelung aufgehoben, da in diesen Jahren das Schaltjahr regulär stattfindet.

Es gilt dann wieder der Regelfall.

Beispiele


Jahr							SB
...	...	...	...	...	...	...	...
1868 (Schaltjahr)		1896^S	entfällt¹⁰⁰ (SB = G)	1908¹⁰⁰ (+12 Jahre)		1936^S	ED
1869	1875^A	1886^B	1897^B	1909¹⁰⁰ (+12 Jahre)	1915^A	1926^B	C
1870	1881^B	1887^A	1898^B	1910¹⁰⁰ (+12 Jahre)	1921^B	1927^A	B
1871	1882^B	1893^B	1899^A	1905¹⁰⁰ (+6 Jahre)	1911^A	1922^B	A
1872 (Schaltjahr)			entfällt¹⁰⁰	1912¹⁰⁰ (+40 Jahre)		1940^S	GF
1873	1879^A	1890^B	1902¹⁰⁰ (+12 Jahre)	1913^B	1919^A	1930^B	E
1874	1885^B	1891^A	1903¹⁰⁰ (+12 Jahre)	1914^B	1925^B	1931^A	D
1875	1886^B	1897^B	1909¹⁰⁰ (+12 Jahre)	1915^A	1926^B	1937^B	C
1876 (Schaltjahr)			entfällt¹⁰⁰ (SB = G)	1916¹⁰⁰ (+40 Jahre)		1944^S	BA
1877	1883^A	1894^B	1900¹⁰⁰ (+6 Jahre)	1906¹⁰⁰ (+6 Jahre)	1917^B	1923^A	G
1878	1889^B	1895^A	1901¹⁰⁰ (+6 Jahre)	1907^A	1918^B	1929^B	F
...	..	...	...	...	...	...	...
1971	1982^B	1993^B	1999^A	2010⁴⁰⁰ (+11 Jahre)	2021^B	2027^A	C
1972 (Schaltjahr)			2000⁴⁰⁰ (+28 Jahre)			2028^S	BA
1973	1979^A	1990^B	2001⁴⁰⁰ (+11 Jahre)	2007^A	2018^B	2029^B	G
1974	1985^B	1991^A	2002⁴⁰⁰ (+11 Jahre)	2013^B	2019^A	2030^B	F
1975	1986^B	1997^B	2003⁴⁰⁰ (+6 Jahre)	2014^B	2025^B	2031^A	E
...	...	...	...	...	...	...	...
2020 (Schaltjahr)			2048^S			2076^S	ED
2021	2027^A	2038^B	2049^B	2055^A	2066^B	2077^B	C
2022	2033^B	2039^A	2050^B	2061^B	2067^A	2078^B	B
2023	2034^B	2045^B	2051^A	2062^B	2073^B	2079^A	A
2024 (Schaltjahr)			2052^S			2080^S	GF
2025	2031^A	2042^B	2053^B	2059^A	2070^B	2081^B	E
...	...	...	...	...	...	...	...
2071	2082^B	2093^B	2099^A	2105¹⁰⁰ (+6 Jahre)	2111^A	2122^B	D
2072 (Schaltjahr)			entfällt¹⁰⁰	2112¹⁰⁰ (+40 Jahre)		2140^S	CB
2073	2079^A	2090^B	2102¹⁰⁰ (+12 Jahre)	2113^B	2119^A	2130^B	A
2074	2085^B	2091^A	2103¹⁰⁰ (+12 Jahre)	2114^B	2125^B	2131^A	G
2075	2086^B	2097^B	2109¹⁰⁰ (+12 Jahre)	2115^A	2126^B	2137^B	F

Legende

SB : Sonntagsbuchstaben (Wochentagszuordnung)

^A Reguläre Wiederholung nach 6 Jahren - 1 Schaltjahr dazwischen

^B Reguläre Wiederholung nach 11 Jahren - 2 Schaltjahre dazwischen

^S Reguläre Schaltjahre Wiederholung nach 28 Jahren

¹⁰⁰ Jahrhundertwechsel-Ausnahme

⁴⁰⁰ Vier-Jahrhundertwechsel-Egalisierung

Geschichte

Nach demselben Prinzip funktionierender „Taschenkalender“ aus Messing für die Jahre 2008–2057; im Bild werden u. a. die Monate Januar, April und Juli 2008 angezeigt

Prinzip eines Drehscheibenkalenders für die Jahre 2001–2028, basierend auf dem Metallkalender des russischen Verlages „Гудок“ aus dem Jahr 1929

Am vielfältigsten haben sich in der Neuzeit die Ewigen Kalender in der Sowjetunion entwickelt. Die Ursache für diese Entwicklung ist in der Einführung des Revolutionskalenders durch den Rat der Volkskommissare im November 1929 zu suchen, mit dem die Wochentagsbezeichnungen zwar noch galten, aber ihre Bedeutung verloren, denn es gab die unterbrochene Fünf-Tage-Woche mit 12 Monaten zu je 30 Tagen sowie 5 arbeitsfreien Tagen. Darauf folgte im November 1931 der Übergang zur Sechs-Tage-Woche und 1940 schließlich wieder die Sieben-Tage-Woche.
Dadurch war wieder das alte Wochentagssystem eingeführt und die Bedeutung des Kalenders – besonders der Ewigen Kalender – stieg stark an. So galt der „Algorithmus zur Ermittlung des Wochentages“ (Kalendertabelle entspricht weitgehend W. Bogatyrjows „таблицу В. Богатырева“ von 1931) in der Sowjetunion als die am bequemsten zu nutzende langfristige Kalendertabelle.^[2] Es erschienen immer neue Ewige Kalender, und die Massenproduktion von Kalendern aus Pappe begann. Diese Pappkalender verfügten jedoch nicht über die für ein für die Ewigkeit gedachtes Produkt benötigte Lebensdauer, sodass in den 1960er Jahren dazu übergegangen wurde, Ewige Kalender aus Aluminium herzustellen; dies waren vor allem Konstruktionen mit Drehscheiben.

So brachte 1929 der russische Verlag „Гудок“ (Gudok) einen Metallkalender heraus.^[3] Er bestand aus einer starren Unterlage, auf der zwei konzentrische Kreise aufgebracht waren, sowie einer drehbaren Scheibe. Auf dem äußeren Kreis waren die Jahreszahlen, auf dem inneren die Wochentage, die sich auf dem Kreis viermal wiederholen, angeordnet. Auf sieben parallelen Feldern der starren Unterlage waren die Monate verzeichnet. Ein Scheibensektor zeigte die Tage 1 bis 31 an, darüber befand sich ein Ausschnitt, in dem die Wochentage sichtbar waren.^[4] In den 1970er Jahren ging man wieder dazu zurück, die Drehscheibenkalender aus Pappe zu fertigen, was allerdings die Nachfrage zurückgehen ließ, sodass zunehmend wieder Kalendertabellen herausgegeben wurden.

Der Zerfall der Sowjetunion zog auch ein Verschwinden der Ewigen Kalender nach sich. Die meisten der noch vorhandenen funktionierten überdies nur bis zum Jahr 2000, sodass sie danach fast ganz verschwanden. Heute setzt man zur Wochentagsberechnung hauptsächlich Computer ein.

Ewiger Julianischer Kalender aus Graubünden (1690)

Als Ewiger Kalender werden auch Algorithmen bezeichnet, welche die Ermittlung des Wochentags an einem vorgegebenen Datum ermöglichen (→ Kalenderrechnung). Auch Tabellen zur Anzeige von Feiertagen, von einem bestimmten Wochentag oder von einem bestimmten Datum (z. B. auf Uhren oder Computern) werden unter dieser Bezeichnung zusammengefasst. Des Weiteren wird bei Kalendern in Computerprogrammen für gewählte Zeiträume – meist Jahre – das Adjektiv „ewig“ verwendet, in Lexika auch „immerwährend“, „Dauer-“ oder „Universal-“.

Der Ausdruck Ewiger Kalender findet auch bei komplexen Uhrwerken von Taschen- oder Armbanduhren^[5]^[6] (Grande Complications) Verwendung, um einen in eine Uhr integrierten Kalendermechanismus zu beschreiben, der „fortwährend“ das korrekte Datum anzeigt und dabei entweder die verschiedenen Längen aller Monate (Halbewiges Kalendarium) oder nur die der Monate mit 30 oder 31 Tagen (der Februar muss dann manuell korrigiert werden) berücksichtigt. Aufwendigere Uhrwerke berücksichtigen zudem die vierjährliche Wiederkehr von Schaltjahren, oft sogar die entsprechenden Ausnahmen in den Jahrhunderten (Ewiges Kalendarium), allerdings nur bis zum 28. Februar 2100.^[7]

Auch bestimmte Kalenderreformen bzw. -entwürfe bezeichnet man als Ewige Kalender, so zum Beispiel den Weltkalender oder den Internationalen Ewigen Kalender (IFC).

Auch für nebenstehende Beispiele ist gemäß Definition die Bezeichnung „Kalender“ nicht gerechtfertigt; wenn den jeweiligen Anweisungen entsprechend der gewünschte Wochentag ermittelt wurde, ist keinesfalls sicher, dass das gefundene Ergebnis stimmt, da es nicht ohne weiteres überprüft werden kann. Man muss das Ergebnis sozusagen glauben, oder man nimmt nach entsprechenden Eingaben in einen Computer den hier angezeigten Wochentag als richtige Vergleichsgröße an.

Siehe auch

Komplikation (Uhrwerk)
Orthodoxer Kalender (Neujulianischer Kalender)

Zur Wochentagsberechnung:

Literatur

Hermann Grotefend: Taschenbuch der Zeitrechnung des deutschen Mittelalters und der Neuzeit. Hahnsche Buchhandlung, Hannover/Leipzig 1915.
Karl Mütz: Faszination Kalender. Polygon-Verlag, Buxheim Eichstätt 1999, ISBN 3-928671-14-6.
Ewige Kalender. In: Hannes E. Schlag: Ein Tag zuviel. Verlag Königshausen & Neumann, Würzburg 1998, ISBN 3-8260-1531-2, S. 128/129.
Ewiger Wochentagskalender. In: Joachim Erlebach: Mathematische Mußestunden. 12. Auflage. De Gruyter, 1964, ISBN 3-11-125868-8, S. 199/200.
Heinz Zemanek: Kalender und Chronologie. 5. Auflage. Oldenbourg-Verlag, 1990, ISBN 3-486-20927-2.
Jürgen Hamel: Kal.rechnung … Gegenwart. Vorträge … Nr. 62 der Archenhold-Sternwarte Berlin-Treptow, 1983.
Elis Strömgren, Bengt Strömgren: Lehrbuch der Astronomie. Berlin 1933.
Ulrich Bastian: Zeit. Das ewige Rätsel. (= Sterne und Weltraum. Special 5). Verlag Sterne und Weltraum, Heidelberg 2000, ISBN 3-87973-502-6. (Faltblattbeilage)
Adolf Weniaminowitsch Butkewitsch, Moisei Samoilowitsch Selikson: Ewige Kalender. (= Kleine naturwissenschaftliche Bibliothek. Band 23). BSB B. G. Teubner Verlagsgesellschaft, Leipzig 1989, ISBN 3-322-00393-0.
Hermann Grotefend: Taschenbuch der Zeitrechnung des deutschen Mittelalters und der Neuzeit. 13. Auflage. Hahn, Hannover 1991, ISBN 3-7752-5177-4.
Steuerberater-Kalender 2013. C. H. Beck, München, ISBN 978-3-406-62919-8, S. 287.

Weblinks

Commons: Ewige Kalender – Sammlung von Bildern, Videos und Audiodateien

Literatur von und über Ewiger Kalender im Katalog der Deutschen Nationalbibliothek
Wikitable perpetual calendars (englisch)
Ewiger Kalender (nach Theodor Wagner) (PDF-Datei; 839 kB)

Einzelnachweise

↑ A. W. Butkewitsch, M. S. Selikson: Ewige Kalender. S. 18 unten/S. 19 oben, Teubner Verlagsgesellschaft, Leipzig 1974.
↑ A. W. Butkewitsch, M. S. Selikson: Ewige Kalender. S. 77.
↑ Металлический календарь с подвижным диском на 28 лет. М., Гудок 1929 (Metallkalender mit drehbarer Scheibe für 28 Jahre).
↑ A. W. Butkewitsch, M. S. Selikson: Ewige Kalender. S. 44 f.
↑ Gisbert L. Brunner: Armbanduhren mit ewigem Kalender. In: Alte Uhren. Heft 4, 1985, S. 41–61.
↑ Gisbert L. Brunner: Der ewige Kalender – Hommage an die Zeit. (Broschüre für Audemars Piguet) Genf / Bad Soden 1994.
↑ Helmut Kahlert, Richard Mühe, Gisbert L. Brunner, Christian Pfeiffer-Belli: Armbanduhren: 100 Jahre Entwicklungsgeschichte. Callwey, München 1983; 5. Auflage. ebenda 1996, ISBN 3-7667-1241-1, S. 504.

[1] A. W. Butkewitsch, M. S. Selikson: Ewige Kalender. S. 18 unten/S. 19 oben, Teubner Verlagsgesellschaft, Leipzig 1974.

[2] A. W. Butkewitsch, M. S. Selikson: Ewige Kalender. S. 77.

[3] Металлический календарь с подвижным диском на 28 лет. М., Гудок 1929 (Metallkalender mit drehbarer Scheibe für 28 Jahre).

[4] A. W. Butkewitsch, M. S. Selikson: Ewige Kalender. S. 44 f.

[5] Gisbert L. Brunner: Armbanduhren mit ewigem Kalender. In: Alte Uhren. Heft 4, 1985, S. 41–61.

[6] Gisbert L. Brunner: Der ewige Kalender – Hommage an die Zeit. (Broschüre für Audemars Piguet) Genf / Bad Soden 1994.

[7] Helmut Kahlert, Richard Mühe, Gisbert L. Brunner, Christian Pfeiffer-Belli: Armbanduhren: 100 Jahre Entwicklungsgeschichte. Callwey, München 1983; 5. Auflage. ebenda 1996, ISBN 3-7667-1241-1, S. 504.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Ewiger Kalender

Inhaltsverzeichnis

Ewiger Gregorianischer Kalender

Ewiger Julianischer und Gregorianischer Kalender